| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
betty
Forumaš(ica)
Pridružen/a: 23. 02. 2006. (19:17:18)
Postovi: (2D)16
|
|
| [Vrh] |
|
tajchi666
Forumaš(ica)

Pridružen/a: 14. 05. 2007. (20:55:39)
Postovi: (2B)16
|
|
| [Vrh] |
|
Malina_1
Forumaš(ica)
Pridružen/a: 26. 01. 2010. (22:06:23)
Postovi: (23)16
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
mona
Forumaš(ica)
Pridružen/a: 27. 05. 2010. (14:16:12)
Postovi: (43)16
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
weirdie
Forumaš(ica)

Pridružen/a: 18. 11. 2005. (15:39:31)
Postovi: (69)16
Spol: 
Lokacija: na svom aršinu prostora
|
 Postano: 22:00 ned, 23. 1. 2011 Naslov: Postano: 22:00 ned, 23. 1. 2011 Naslov: |
    |
|
|
[quote="Milojko"]
@weirdie:
moraš provjerit jedino uvjet kad je cosx=0, jer imaš da je dy/(2-y)= tgxdx, jer je 1/ctgx = tgx. prvo riješiš normalno na domenama gdje cosx nije nula, i onda pogledaš dal se može proširit za cosx = 0, i onda dobiš da je y(pi/2+kpi) = 2, k cijeli broj[/quote]
Nisam sigurna jesam li shvatila ovo tvoje rješenje:
Ja sam dobila: y=2-C*cosx, za C realan.
E sad, ako gledam posebno rješenje kad ctgx=0, dobijem još jedno rješenje: a to je kad x=pi/2 + k*pi, a ako takav x ubacim u jdbu, dobijem y=2, ali to je već obuhvaćeno sa y=2 - C*cosx, C realan.
Pa mi nije jasno što si ti dobio i nije mi jasno dal kad postoji neki uvjet dijeljenja jdbe sa izrazom koji uključuje samo x, treba li to provjeravati?
I da, za zadatak2 iz 1.klkija, napisala sam krivo krajnje rješenje.
Mislim da bi pravo trebalo biti: y^3=x*sqrt(2*x-1) i y^3=-x*sqrt(2*x-1)
| Milojko (napisa): |
@weirdie:
moraš provjerit jedino uvjet kad je cosx=0, jer imaš da je dy/(2-y)= tgxdx, jer je 1/ctgx = tgx. prvo riješiš normalno na domenama gdje cosx nije nula, i onda pogledaš dal se može proširit za cosx = 0, i onda dobiš da je y(pi/2+kpi) = 2, k cijeli broj |
Nisam sigurna jesam li shvatila ovo tvoje rješenje:
Ja sam dobila: y=2-C*cosx, za C realan.
E sad, ako gledam posebno rješenje kad ctgx=0, dobijem još jedno rješenje: a to je kad x=pi/2 + k*pi, a ako takav x ubacim u jdbu, dobijem y=2, ali to je već obuhvaćeno sa y=2 - C*cosx, C realan.
Pa mi nije jasno što si ti dobio i nije mi jasno dal kad postoji neki uvjet dijeljenja jdbe sa izrazom koji uključuje samo x, treba li to provjeravati?
I da, za zadatak2 iz 1.klkija, napisala sam krivo krajnje rješenje.
Mislim da bi pravo trebalo biti: y^3=x*sqrt(2*x-1) i y^3=-x*sqrt(2*x-1)
_________________
don't let them change ya!
or even rearrange ya!
we've got a life to live. they say: only-only-only th fittest of the fittest shall survive!
stay alive! eh!
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Malina_1
Forumaš(ica)
Pridružen/a: 26. 01. 2010. (22:06:23)
Postovi: (23)16
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 0:17 pon, 24. 1. 2011 Naslov: Postano: 0:17 pon, 24. 1. 2011 Naslov: |
    |
|
|
[quote="Anonymous"]COBS:
podijelis prvo sa x jednadzbu,
napravis supstituciju y=z^m, y'=m*z^m-1*z' i uvrstis
Dobis:
2z^3m+3x- (6z^5m*m*z^(m-1) + 3x*z^2m*m*z^(m-1))*z'=0
sada gledas potencije svakog izraza gdje z' nema "nikakvu tezinu" pa imas
3m=1=5m+m-1=2m+m-1+1
Iz ovoga slijedi da je m=1/3
Jesi rijesio 4 zadatak s kolokvija iz ove godine
Dobim y-y'x=8sqrt(x^2+y^2) i to se da jos malo sredivati, ali ne uspijem doci do lijepog izraza...[/quote]
e da... znači tam di imam z' gledam posebno i to izjednačavam sa onim di nemam z' ( a još posebno izjednačavam s onim di mi je sam x? )
ok, onda dobijem m i kaj mi to znači?, uzimam supstituciju z = y^3?
ak da, jel može još red ili dva... ak ne niš od sveg toga...
ovaj 4.
znači odmah se dobije da je:
[latex]8\sqrt{ x^2 + y^2 } = y - y'x[/latex]
sve podijeliš s x i dobiješ:
[latex]8\sqrt{\frac{y^2}{x^2} + 1} = \frac{y}{x} - y'[/latex]
sad ide supstitucija z = y/x, dalje nije teško ( javi ak treba raspisat )
EDIT: i još što se tiče 5. - ih zadataka općenito, sam trebamo gledat dal je funkcija Lipschitzova po drugoj varijabli? ili još nešto drugo?
| Anonymous (napisa): | COBS:
podijelis prvo sa x jednadzbu,
napravis supstituciju y=z^m, y'=m*z^m-1*z' i uvrstis
Dobis:
2z^3m+3x- (6z^5m*m*z^(m-1) + 3x*z^2m*m*z^(m-1))*z'=0
sada gledas potencije svakog izraza gdje z' nema "nikakvu tezinu" pa imas
3m=1=5m+m-1=2m+m-1+1
Iz ovoga slijedi da je m=1/3
Jesi rijesio 4 zadatak s kolokvija iz ove godine
Dobim y-y'x=8sqrt(x^2+y^2) i to se da jos malo sredivati, ali ne uspijem doci do lijepog izraza... |
e da... znači tam di imam z' gledam posebno i to izjednačavam sa onim di nemam z' ( a još posebno izjednačavam s onim di mi je sam x? )
ok, onda dobijem m i kaj mi to znači?, uzimam supstituciju z = y^3?
ak da, jel može još red ili dva... ak ne niš od sveg toga...
ovaj 4.
znači odmah se dobije da je:
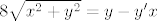
sve podijeliš s x i dobiješ:
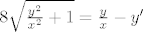
sad ide supstitucija z = y/x, dalje nije teško ( javi ak treba raspisat )
EDIT: i još što se tiče 5. - ih zadataka općenito, sam trebamo gledat dal je funkcija Lipschitzova po drugoj varijabli? ili još nešto drugo?
|
|
| [Vrh] |
|
Gost
|
 Postano: 0:42 pon, 24. 1. 2011 Naslov: Postano: 0:42 pon, 24. 1. 2011 Naslov: |
    |
|
|
Dok ja raspisem ovaj 4. nakon integriranja dobim
8ln(z+sqrt(1+z^2)) = -ln|x|+lnC
pa je to
(z+sqrt(1+z^2)^8 = C * x^-1
i sto sad???
Sto se tice ovoga tvojega.
Sablona je otprilike ovakva:
1. pogledas da li se jednadzba da pojednostaviti, ako imas dx i dy rastavljene moras ih spojiti jer inace ne mozes dalje, kada ih spojis i dobis y' ako je na primjer y'(f(x)+g(x)) napises u obliku y'*f(x)+y'g(x)
2. UVIJEK (ako mislis da je to ta supstitucija koju trebas) zamijenis y=z^m, i y'=m*z^(m-1)*z'
i uvrstis u jednadzbu umjesto y
3. Dobis jednadzbu koja izgleda uvijek otprilike ovako:
f1(x,y)+f2(x,y)+...= y'*f3(x,y)+y'*f4(x,y)
to jest
g1(x,z)+g2(x,z)+...= m*z^(m-1)*z'*g3(x,z) + m*z^(m-1)*z'*g4(x,z)
I sada je poanta u tome da usporedujes potencije svake funkcije, recimo za x^5*z^2m imamo 5+2m, za x^2 imamo 2,
za m * z^(m-1) * z' * x^2 * z^(3m) imamo m-1+2+3m
I sve ih izjednacimo i ako imamo srece dobijemo m
DA, i na kraju uzmes supstituciju z=y^3 u ovom primjeru i sve ti se fino pokrati.
Dok ja raspisem ovaj 4. nakon integriranja dobim
8ln(z+sqrt(1+z^2)) = -ln|x|+lnC
pa je to
(z+sqrt(1+z^2)^8 = C * x^-1
i sto sad???
Sto se tice ovoga tvojega.
Sablona je otprilike ovakva:
1. pogledas da li se jednadzba da pojednostaviti, ako imas dx i dy rastavljene moras ih spojiti jer inace ne mozes dalje, kada ih spojis i dobis y' ako je na primjer y'(f(x)+g(x)) napises u obliku y'*f(x)+y'g(x)
2. UVIJEK (ako mislis da je to ta supstitucija koju trebas) zamijenis y=z^m, i y'=m*z^(m-1)*z'
i uvrstis u jednadzbu umjesto y
3. Dobis jednadzbu koja izgleda uvijek otprilike ovako:
f1(x,y)+f2(x,y)+...= y'*f3(x,y)+y'*f4(x,y)
to jest
g1(x,z)+g2(x,z)+...= m*z^(m-1)*z'*g3(x,z) + m*z^(m-1)*z'*g4(x,z)
I sada je poanta u tome da usporedujes potencije svake funkcije, recimo za x^5*z^2m imamo 5+2m, za x^2 imamo 2,
za m * z^(m-1) * z' * x^2 * z^(3m) imamo m-1+2+3m
I sve ih izjednacimo i ako imamo srece dobijemo m
DA, i na kraju uzmes supstituciju z=y^3 u ovom primjeru i sve ti se fino pokrati.
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
Gost
|
 Postano: 1:23 pon, 24. 1. 2011 Naslov: Postano: 1:23 pon, 24. 1. 2011 Naslov: |
    |
|
|
OK, fala, to pise i u tablici integrala, nadam se da budu nam dali da imamo papir s formulama, buduci da budu ovi za 2. kolokvij smijeli imati:D
Dobije se y=x*sh(-8ln(x)+C)
za T=(1,0) ispada
C=0, na kraju
y=x*sh(-8ln(x), x>0
OK, fala, to pise i u tablici integrala, nadam se da budu nam dali da imamo papir s formulama, buduci da budu ovi za 2. kolokvij smijeli imati:D
Dobije se y=x*sh(-8ln(x)+C)
za T=(1,0) ispada
C=0, na kraju
y=x*sh(-8ln(x), x>0
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 1:26 pon, 24. 1. 2011 Naslov: Postano: 1:26 pon, 24. 1. 2011 Naslov: |
    |
|
|
[quote="Anonymous"]OK, fala, to pise i u tablici integrala, nadam se da budu nam dali da imamo papir s formulama, buduci da budu ovi za 2. kolokvij smijeli imati:D
Dobije se y=x*sh(-8ln(x)+C)
za T=(1,0) ispada
C=0, na kraju
y=x*sh(-8ln(x), x>0[/quote]
na kolokviju budi brutalan i ovo rješenje još raspiši do kraja:
[latex]sh(x) = \frac{e^x - e^{-x}}{2}[/latex]
to uvrstiš i brijem da možda dobiješ nešto još ljepše? ( nisam gledo )
Ako bi netko mogao napisati za 5. zadatak samo rješenja ako ima ( može li se ili ne može primjeniti određeni teorem, samo da ili ne ).
| Anonymous (napisa): | OK, fala, to pise i u tablici integrala, nadam se da budu nam dali da imamo papir s formulama, buduci da budu ovi za 2. kolokvij smijeli imati:D
Dobije se y=x*sh(-8ln(x)+C)
za T=(1,0) ispada
C=0, na kraju
y=x*sh(-8ln(x), x>0 |
na kolokviju budi brutalan i ovo rješenje još raspiši do kraja:
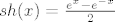
to uvrstiš i brijem da možda dobiješ nešto još ljepše? ( nisam gledo )
Ako bi netko mogao napisati za 5. zadatak samo rješenja ako ima ( može li se ili ne može primjeniti određeni teorem, samo da ili ne ).
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 16:16 pon, 24. 1. 2011 Naslov: Postano: 16:16 pon, 24. 1. 2011 Naslov: |
    |
|
|
(x+y+1)(x+y+2)dy=(x^2+2xy+y^2)dx
možel to netko riješit?
(x+y+1)(x+y+2)dy=(x^2+2xy+y^2)dx
možel to netko riješit?
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Anja
Forumaš(ica)


Pridružen/a: 24. 03. 2003. (10:51:07)
Postovi: (132)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Anja
Forumaš(ica)


Pridružen/a: 24. 03. 2003. (10:51:07)
Postovi: (132)16
|
|
| [Vrh] |
|
|











