| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
googol
Forumaš(ica)


Pridružen/a: 29. 09. 2011. (21:23:09)
Postovi: (71)16
Spol: 
|
 Postano: 0:03 sri, 10. 4. 2013 Naslov: Postano: 0:03 sri, 10. 4. 2013 Naslov: |
    |
|
|
[quote="Lafiel"][quote="Anonymous"]Molim te raspisi![/quote]
Kao što je Megy Poe rekla, gledaš marginalne distribucije pa imaš da ti se ocjene iz kemije (X) pojavljuju 12 puta trojka, 14 puta četvorka i 12 puta petica, a ocjene iz biologije (Y) 9 puta trojka, 20 puta četvorka i 9 puta petica.
a) Relativne frekvencije za X su ti redom [tex]\frac{12}{38}[/tex], [tex]\frac{14}{38}[/tex] i [tex]\frac{12}{38}[/tex].
b) [tex]\overline{x}=\frac{12*3+14*4+12*5}{38}, \overline{y}=\frac{9*3+20*4+9*5}{38}[/tex]
c) Po tim marginalnima onda računaš i [tex]S_{xx}[/tex] i [tex]S_{yy}[/tex].
d) Za [tex]S_{xy}[/tex] ti trebaju "kombinacije" [tex]x_{i}y_{i}[/tex] i to svako njihovo pojavljivanje u uzorku (npr. par (3,3) pronalazimo kod 5 studenata) pa računaš
[tex]S_{xy}=5*3*3+5*3*4+2*3*5+2*4*3+10*4*4+2*5*4+2*5*3+5*5*4+5*5*5 - 38*\overline{x}*\overline{y}[/tex][/quote]
Pohvala! Molim te jos mi samo raspisi [latex]S_{x x}[/latex]. Puno hvala!
| Lafiel (napisa): | | Anonymous (napisa): | | Molim te raspisi! |
Kao što je Megy Poe rekla, gledaš marginalne distribucije pa imaš da ti se ocjene iz kemije (X) pojavljuju 12 puta trojka, 14 puta četvorka i 12 puta petica, a ocjene iz biologije (Y) 9 puta trojka, 20 puta četvorka i 9 puta petica.
a) Relativne frekvencije za X su ti redom [tex]\frac{12}{38}[/tex], [tex]\frac{14}{38}[/tex] i [tex]\frac{12}{38}[/tex].
b) [tex]\overline{x}=\frac{12*3+14*4+12*5}{38}, \overline{y}=\frac{9*3+20*4+9*5}{38}[/tex]
c) Po tim marginalnima onda računaš i [tex]S_{xx}[/tex] i [tex]S_{yy}[/tex].
d) Za [tex]S_{xy}[/tex] ti trebaju "kombinacije" [tex]x_{i}y_{i}[/tex] i to svako njihovo pojavljivanje u uzorku (npr. par (3,3) pronalazimo kod 5 studenata) pa računaš
[tex]S_{xy}=5*3*3+5*3*4+2*3*5+2*4*3+10*4*4+2*5*4+2*5*3+5*5*4+5*5*5 - 38*\overline{x}*\overline{y}[/tex] |
Pohvala! Molim te jos mi samo raspisi 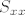 . Puno hvala! . Puno hvala!
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 7:54 pet, 31. 5. 2013 Naslov: Postano: 7:54 pet, 31. 5. 2013 Naslov: |
    |
|
|
[quote="Megy Poe"]Kako se riješava 3 zadatak pod a i b iz proslogodišnjeg kolokvija?
http://web.math.pmf.unizg.hr/nastava/stat/files/stat-1112-kol2_rjes.pdf[/quote]
U (a) prvo nađeš MLE za [tex]\theta[/tex], pa ga kvadriraš da dobiš MLE za [tex]\theta^2[/tex].
Uvijek, uz bilo koju distribuciju s konačnim očekivanjem, je [tex]\overline{X}_n[/tex] nepristrani procjenitelj za očekivanje te distribucije. U (b) je zato [tex]\overline{X}_n[/tex] nepristrani procjenitelj za [tex]\frac{1 + \theta}{2}[/tex], tj. [tex]\mathbb{E}_\theta \overline{X}_n = \frac{1 + \theta}{2}[/tex]. Slijedi da je [tex]2 \overline{X}_n - 1[/tex] nepristrani procjenitelj za [tex]\theta[/tex], jer vrijedi [tex]\mathbb{E}_\theta[2 \overline{X}_n + 1] = \theta[/tex].
U (a) prvo nađeš MLE za [tex]\theta[/tex], pa ga kvadriraš da dobiš MLE za [tex]\theta^2[/tex].
Uvijek, uz bilo koju distribuciju s konačnim očekivanjem, je [tex]\overline{X}_n[/tex] nepristrani procjenitelj za očekivanje te distribucije. U (b) je zato [tex]\overline{X}_n[/tex] nepristrani procjenitelj za [tex]\frac{1 + \theta}{2}[/tex], tj. [tex]\mathbb{E}_\theta \overline{X}_n = \frac{1 + \theta}{2}[/tex]. Slijedi da je [tex]2 \overline{X}_n - 1[/tex] nepristrani procjenitelj za [tex]\theta[/tex], jer vrijedi [tex]\mathbb{E}_\theta[2 \overline{X}_n + 1] = \theta[/tex].
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
 Postano: 15:01 pet, 31. 5. 2013 Naslov: Postano: 15:01 pet, 31. 5. 2013 Naslov: |
    |
|
|
[quote="pmli"][quote="Megy Poe"]Kako se riješava 3 zadatak pod a i b iz proslogodišnjeg kolokvija?
http://web.math.pmf.unizg.hr/nastava/stat/files/stat-1112-kol2_rjes.pdf[/quote]
U (a) prvo nađeš MLE za [tex]\theta[/tex], pa ga kvadriraš da dobiš MLE za [tex]\theta^2[/tex].
Uvijek, uz bilo koju distribuciju s konačnim očekivanjem, je [tex]\overline{X}_n[/tex] nepristrani procjenitelj za očekivanje te distribucije. U (b) je zato [tex]\overline{X}_n[/tex] nepristrani procjenitelj za [tex]\frac{1 + \theta}{2}[/tex], tj. [tex]\mathbb{E}_\theta \overline{X}_n = \frac{1 + \theta}{2}[/tex]. Slijedi da je [tex]2 \overline{X}_n - 1[/tex] nepristrani procjenitelj za [tex]\theta[/tex], jer vrijedi [tex]\mathbb{E}_\theta[2 \overline{X}_n + 1] = \theta[/tex].[/quote]
Hvala! Samo bi mogo još objasniti u 4.18 zad s vježbi b)
http://web.math.pmf.unizg.hr/nastava/stat/files/chap4_novo.pdf
Zašto se za nepristrani procjenitelj uzima n-1/Y a ne n/Y?
Također neznam u zadacima 4.15, 4.16 treba računati MLE za bernulija..
Al ja neznam kak ta funkcija izgleda i onda ne znam riješiti ni jedan od ta dva :/
| pmli (napisa): |
U (a) prvo nađeš MLE za [tex]\theta[/tex], pa ga kvadriraš da dobiš MLE za [tex]\theta^2[/tex].
Uvijek, uz bilo koju distribuciju s konačnim očekivanjem, je [tex]\overline{X}_n[/tex] nepristrani procjenitelj za očekivanje te distribucije. U (b) je zato [tex]\overline{X}_n[/tex] nepristrani procjenitelj za [tex]\frac{1 + \theta}{2}[/tex], tj. [tex]\mathbb{E}_\theta \overline{X}_n = \frac{1 + \theta}{2}[/tex]. Slijedi da je [tex]2 \overline{X}_n - 1[/tex] nepristrani procjenitelj za [tex]\theta[/tex], jer vrijedi [tex]\mathbb{E}_\theta[2 \overline{X}_n + 1] = \theta[/tex]. |
Hvala! Samo bi mogo još objasniti u 4.18 zad s vježbi b)
http://web.math.pmf.unizg.hr/nastava/stat/files/chap4_novo.pdf
Zašto se za nepristrani procjenitelj uzima n-1/Y a ne n/Y?
Također neznam u zadacima 4.15, 4.16 treba računati MLE za bernulija..
Al ja neznam kak ta funkcija izgleda i onda ne znam riješiti ni jedan od ta dva 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 18:37 pet, 31. 5. 2013 Naslov: Postano: 18:37 pet, 31. 5. 2013 Naslov: |
    |
|
|
[quote="Megy Poe"]Hvala! Samo bi mogo još objasniti u 4.18 zad s vježbi b)
http://web.math.pmf.unizg.hr/nastava/stat/files/chap4_novo.pdf
Zašto se za nepristrani procjenitelj uzima n-1/Y a ne n/Y?[/quote]
Vrijedi [tex]\mathbb{E}_\lambda[\frac{Y}{n}] = \frac{1}{\lambda}[/tex], ali iz toga ne možeš zaključiti da je [tex]\mathbb{E}_\lambda[\frac{n}{Y}] = \lambda[/tex] jer se ne radi o linearnoj transformaciji. Mislim da ovdje jednostavno trebaš pogoditi da je rješenje neka konstanta puta [tex]\frac{1}{Y}[/tex] (što ima nekog smisla, jer je MLE tog oblika), pa odrediti tu konstatnu iz uvjeta [tex]\mathbb{E}_\lambda[\frac{C}{Y}] = \lambda[/tex].
[quote="Megy Poe"]Također neznam u zadacima 4.15, 4.16 treba računati MLE za bernulija..
Al ja neznam kak ta funkcija izgleda i onda ne znam riješiti ni jedan od ta dva :/[/quote]
Najbolje je koristiti izraz [tex]p^x (1 - p)^{1 - x}[/tex] za funkciju gustoće Bernoullijeve sl. var. (pritom [tex]x[/tex] može biti 0 ili 1). U 4.15 koristiš da je očekivanje [tex]p[/tex] i da je varijanca [tex]p (1 - p)[/tex] kad ti se kombinacije tih izraza pojavljuju (kao u (a) dijelu), dok u kompliciranijim slučajevima koristiš [tex]\mathbb{E}[1_A] = \mathbb{P}(A)[/tex] (kao u (b) dijelu).
Vrijedi [tex]\mathbb{E}_\lambda[\frac{Y}{n}] = \frac{1}{\lambda}[/tex], ali iz toga ne možeš zaključiti da je [tex]\mathbb{E}_\lambda[\frac{n}{Y}] = \lambda[/tex] jer se ne radi o linearnoj transformaciji. Mislim da ovdje jednostavno trebaš pogoditi da je rješenje neka konstanta puta [tex]\frac{1}{Y}[/tex] (što ima nekog smisla, jer je MLE tog oblika), pa odrediti tu konstatnu iz uvjeta [tex]\mathbb{E}_\lambda[\frac{C}{Y}] = \lambda[/tex].
| Megy Poe (napisa): | Također neznam u zadacima 4.15, 4.16 treba računati MLE za bernulija..
Al ja neznam kak ta funkcija izgleda i onda ne znam riješiti ni jedan od ta dva  |
Najbolje je koristiti izraz [tex]p^x (1 - p)^{1 - x}[/tex] za funkciju gustoće Bernoullijeve sl. var. (pritom [tex]x[/tex] može biti 0 ili 1). U 4.15 koristiš da je očekivanje [tex]p[/tex] i da je varijanca [tex]p (1 - p)[/tex] kad ti se kombinacije tih izraza pojavljuju (kao u (a) dijelu), dok u kompliciranijim slučajevima koristiš [tex]\mathbb{E}[1_A] = \mathbb{P}(A)[/tex] (kao u (b) dijelu).
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 13:28 sub, 1. 6. 2013 Naslov: Postano: 13:28 sub, 1. 6. 2013 Naslov: |
    |
|
|
[quote="Anonymous"]Je li testna statistika u zadnjem zadatku proslogodisnjeg kolokvija (prva grupa) ispadne 2/3 a ne 7/3 kao sto je u rjesenjima?[/quote]
Također mi ispada 2/3.
[quote="Lafiel"]Možeš li mi to malo pojasniti, molim te? Zadatak 5.6. rješavali smo uz pretpostavku da su vrijednosti normalno distribuirane i da imaju jednaku varijancu, no nijednu od te dvije pretpostavke nemamo u ovom zadatku. Možemo li obje zanemariti i zašto?[/quote]
U 5.14 su veliki uzorci, pa će testna statistika imati približno distribuciju kao kad su podaci normalno distribuirani. Jednakost varijance s može provjeriti f-testom, ali to se ne traži u zadatku, pa nije potrebno (samo uzmeš da vrijedi ta pretpostavka). Najbolje pitati na kolokviju profesora/asistenta ako uočiš tako nešto. Osobno, uzeo bih da te pretpostavke vrijede bez ikakve napomene, jer što ćeš inače? :D
| Anonymous (napisa): | | Je li testna statistika u zadnjem zadatku proslogodisnjeg kolokvija (prva grupa) ispadne 2/3 a ne 7/3 kao sto je u rjesenjima? |
Također mi ispada 2/3.
| Lafiel (napisa): | | Možeš li mi to malo pojasniti, molim te? Zadatak 5.6. rješavali smo uz pretpostavku da su vrijednosti normalno distribuirane i da imaju jednaku varijancu, no nijednu od te dvije pretpostavke nemamo u ovom zadatku. Možemo li obje zanemariti i zašto? |
U 5.14 su veliki uzorci, pa će testna statistika imati približno distribuciju kao kad su podaci normalno distribuirani. Jednakost varijance s može provjeriti f-testom, ali to se ne traži u zadatku, pa nije potrebno (samo uzmeš da vrijedi ta pretpostavka). Najbolje pitati na kolokviju profesora/asistenta ako uočiš tako nešto. Osobno, uzeo bih da te pretpostavke vrijede bez ikakve napomene, jer što ćeš inače? 
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
aboll
Forumaš(ica)

Pridružen/a: 22. 10. 2012. (09:12:16)
Postovi: (3)16
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
|
| [Vrh] |
|
|













