| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 11:35 pon, 24. 11. 2008 Naslov: Postano: 11:35 pon, 24. 11. 2008 Naslov: |
    |
|
|
Ja mislim da to ide nekako ovako, ali nisam 100% siguran :), mislim da se to nije na vježbama radilo...
Pokazati ću na konkretnom primjeru, tada je lako poopćiti ideju... nadam se :)
[b]Uvod u računarstvo - 1. kolokvij, 26. 11. 2004., prvi zadatak pod b[/b]
Metodom dvojnog komplementa izračunajte razliku [latex]\left(101100010\right)_2 - \left(101110\right)_2[/latex] .
Sada zamislimo da imamo računalo s registrom od [b]10[/b] bitova. U njemu je broj [latex]101100010[/latex] prikazan kao [latex]0101100010[/latex], a broj [latex]101110[/latex] kao [latex]0000101110[/latex] .
Dvojni komplement broja [latex]101110[/latex] u tom računalu je broj [latex]1111010010[/latex], odnosno, u tom računalu je [latex]1111010010 = - 0000101110[/latex] (prvi bit je naravno bit za predznak).
Sada je u tom računalu [latex]\left(101100010\right)_2 - \left(101110\right)_2 = 0101100010 + 1111010010 = 0100110100[/latex].
Dakle, konačno [latex]\left(101100010\right)_2 - \left(101110\right)_2 = \left(100110100\right)_2[/latex] .
Zbroj binarnih brojeva [latex]0101100010[/latex] [b]i[/b] [latex]1111010010[/latex] je binarni broj [latex]10100110100[/latex], no on ima [b]11[/b] bitova, pa prvi bit "otpada" (jer radimo s računalom koje ima registar od [b]10[/b] bitova).
Nadam se da je dobro... :-)
Također se nadam da sam uspio pojasniti...
Ja mislim da to ide nekako ovako, ali nisam 100% siguran  , mislim da se to nije na vježbama radilo... , mislim da se to nije na vježbama radilo...
Pokazati ću na konkretnom primjeru, tada je lako poopćiti ideju... nadam se 
Uvod u računarstvo - 1. kolokvij, 26. 11. 2004., prvi zadatak pod b
Metodom dvojnog komplementa izračunajte razliku 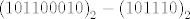 . .
Sada zamislimo da imamo računalo s registrom od 10 bitova. U njemu je broj 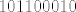 prikazan kao prikazan kao 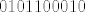 , a broj , a broj  kao kao 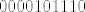 . .
Dvojni komplement broja  u tom računalu je broj u tom računalu je broj  , odnosno, u tom računalu je , odnosno, u tom računalu je 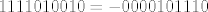 (prvi bit je naravno bit za predznak). (prvi bit je naravno bit za predznak).
Sada je u tom računalu 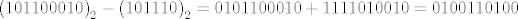 . .
Dakle, konačno 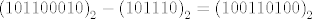 . .
Zbroj binarnih brojeva 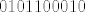 i i  je binarni broj je binarni broj  , no on ima 11 bitova, pa prvi bit "otpada" (jer radimo s računalom koje ima registar od 10 bitova). , no on ima 11 bitova, pa prvi bit "otpada" (jer radimo s računalom koje ima registar od 10 bitova).
Nadam se da je dobro... 
Također se nadam da sam uspio pojasniti...
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 19:31 pon, 24. 11. 2008 Naslov: Postano: 19:31 pon, 24. 11. 2008 Naslov: |
    |
|
|
jedi sarmu, etotna!!
jedi sarmu, etotna!!
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
bbroj
Forumaš(ica)

Pridružen/a: 11. 02. 2008. (17:17:24)
Postovi: (49)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 22:00 čet, 2. 4. 2009 Naslov: Postano: 22:00 čet, 2. 4. 2009 Naslov: |
    |
|
|
[quote="bbroj"]moze li mi netko molim vas napisat algoritam za pronalazenje prostih djelitelja nekog broja..?? :oops:
...bez koristenja nizova...[/quote]
Pa onako kako bi išo "na ruke"...
1. učitaš broj (nazovimo ga x)
2. ideš po brojevima koji su manji od x (dovoljno do korijen iz x, nijedan prosti djelitelj neće bit već od toga)
3. ako je taj djelitelj prost i dijeli x onda je on prosti djelitelj!
[code:1]
int prost( int n ) //fja provjerava dal je n prost
{
int i;
for (i=2;i<=sqrt(n);i++)
if ( n%i ==0 ) return 0;
return 1;
}
int main()
{
int x,i;
scanf("%d",&x);
printf("Prosti djelitelji od %d: ",x);
for (i=2;i<=x;i++) //sa petljom idem do x jer to pokriva slučaj da je x prost
if ( x%i==0 && prost(i) ) printf (" %d ",i);
return 0;
}
[/code:1]
| bbroj (napisa): | moze li mi netko molim vas napisat algoritam za pronalazenje prostih djelitelja nekog broja..?? 
...bez koristenja nizova... |
Pa onako kako bi išo "na ruke"...
1. učitaš broj (nazovimo ga x)
2. ideš po brojevima koji su manji od x (dovoljno do korijen iz x, nijedan prosti djelitelj neće bit već od toga)
3. ako je taj djelitelj prost i dijeli x onda je on prosti djelitelj!
| Kod: |
int prost( int n ) //fja provjerava dal je n prost
{
int i;
for (i=2;i<=sqrt(n);i++)
if ( n%i ==0 ) return 0;
return 1;
}
int main()
{
int x,i;
scanf("%d",&x);
printf("Prosti djelitelji od %d: ",x);
for (i=2;i<=x;i++) //sa petljom idem do x jer to pokriva slučaj da je x prost
if ( x%i==0 && prost(i) ) printf (" %d ",i);
return 0;
}
|
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
bbroj
Forumaš(ica)

Pridružen/a: 11. 02. 2008. (17:17:24)
Postovi: (49)16
|
 Postano: 22:41 čet, 2. 4. 2009 Naslov: Postano: 22:41 čet, 2. 4. 2009 Naslov: |
    |
|
|
[quote="Luuka"][quote="bbroj"]moze li mi netko molim vas napisat algoritam za pronalazenje prostih djelitelja nekog broja..?? :oops:
...bez koristenja nizova...[/quote]
Pa onako kako bi išo "na ruke"...
1. učitaš broj (nazovimo ga x)
2. ideš po brojevima koji su manji od x (dovoljno do korijen iz x, nijedan prosti djelitelj neće bit već od toga)
3. ako je taj djelitelj prost i dijeli x onda je on prosti djelitelj!
[code:1]
int prost( int n ) //fja provjerava dal je n prost
{
int i;
for (i=2;i<=sqrt(n);i++)
if ( n%i ==0 ) return 0;
return 1;
}
int main()
{
int x,i;
scanf("%d",&x);
printf("Prosti djelitelji od %d: ",x);
for (i=2;i<=x;i++) //sa petljom idem do x jer to pokriva slučaj da je x prost
if ( x%i==0 && prost(i) ) printf (" %d ",i);
return 0;
}
e da,zaboravio sam napomenuti da ne smijem koristiti fje iz math.h,tj korijene itd... pa ako mi mozes jos to prepraviti....u svakom slucaju hvala!
[/code:1][/quote]
| Luuka (napisa): | | bbroj (napisa): | moze li mi netko molim vas napisat algoritam za pronalazenje prostih djelitelja nekog broja..?? 
...bez koristenja nizova... |
Pa onako kako bi išo "na ruke"...
1. učitaš broj (nazovimo ga x)
2. ideš po brojevima koji su manji od x (dovoljno do korijen iz x, nijedan prosti djelitelj neće bit već od toga)
3. ako je taj djelitelj prost i dijeli x onda je on prosti djelitelj!
| Kod: |
int prost( int n ) //fja provjerava dal je n prost
{
int i;
for (i=2;i<=sqrt(n);i++)
if ( n%i ==0 ) return 0;
return 1;
}
int main()
{
int x,i;
scanf("%d",&x);
printf("Prosti djelitelji od %d: ",x);
for (i=2;i<=x;i++) //sa petljom idem do x jer to pokriva slučaj da je x prost
if ( x%i==0 && prost(i) ) printf (" %d ",i);
return 0;
}
e da,zaboravio sam napomenuti da ne smijem koristiti fje iz math.h,tj korijene itd... pa ako mi mozes jos to prepraviti....u svakom slucaju hvala!
|
|
|
|
| [Vrh] |
|
Spectre
Forumaš(ica)


Pridružen/a: 02. 10. 2006. (16:58:05)
Postovi: (167)16
Spol: 
|
|
| [Vrh] |
|
|
















