| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 13:18 čet, 9. 6. 2011 Naslov: Postano: 13:18 čet, 9. 6. 2011 Naslov: |
    |
|
|
malos zabrijo. na predavanjima je urađeno bilo do 6.7 ili tako nešto
malos zabrijo. na predavanjima je urađeno bilo do 6.7 ili tako nešto
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Charmed
Forumaš(ica)


Pridružen/a: 22. 02. 2009. (11:51:49)
Postovi: (20B)16
Spol: 
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Charmed
Forumaš(ica)


Pridružen/a: 22. 02. 2009. (11:51:49)
Postovi: (20B)16
Spol: 
|
|
| [Vrh] |
|
tomitza
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
 Postano: 13:01 ned, 3. 7. 2011 Naslov: Postano: 13:01 ned, 3. 7. 2011 Naslov: |
    |
|
|
[quote="Anonymous"]Molim vas, može li mi netko objasniti razliku između [b]biti element [/b]i [b]biti podskup[/b] nekog skupa. (Ako može, molim i primjer iz kojeg se to vidi)
Unaprijed hvala![/quote]
Neka je [latex]X[/latex] neki skup.
[latex]A \subset X \; ako \;\forall a\in A \Rightarrow a\in X[/latex]
Posebno, podskup mora biti skup.
[latex]Neka\;je\;X=\left \{ 1,2,3,4 \right \}[/latex]
[latex]Tada\;je\;A=\left \{ 1,2,3 \right \} \;podskup\;od\;X[/latex]
[latex]Takoder\;B=\left \{ 1 \right \} \;je\;podskup\;od\;X[/latex]
Dakle ovdje se radi o skupu koji ima samo jedan član. Kad ti ti piše [latex]1 \in X [/latex], to nije isto kao da piše [latex]\left \{ 1 \right \} \subset X[/latex], jer se u drugom slučaju radi o skupu, dok ovo prvo to nije.
Ono što tebe sigurno zbunjuje, je zašto kod nekih familija podskupova nekog skupa(algebri, prstenova...) piše za neke skupove, npr. [latex]A \in \sigma (\mathbb{R} ) [/latex]
Nije precizna definicija, ali koristit ce, familije podskupova nekog skupa za svoje elemente imaju podskupove tog skupa. Uzmimo partitivni skup. Vrijedi ovo:
[latex] A \in \mathit{P}(X) \Leftrightarrow A \subset X [/latex]
E sad, neka je npr. [latex]\sigma[/latex] familija podskupova od X. Tada [latex]\sigma[/latex] sadrži podskupove od X. Posebno, vrijedi [latex]\sigma \subset \mathit{P}(X)[/latex], ali ne vrijedi [latex]\sigma \subset X[/latex].
Nadam se da sam razjasnio :D
| Anonymous (napisa): | Molim vas, može li mi netko objasniti razliku između biti element i biti podskup nekog skupa. (Ako može, molim i primjer iz kojeg se to vidi)
Unaprijed hvala! |
Neka je  neki skup. neki skup.

Posebno, podskup mora biti skup.
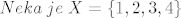
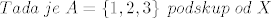

Dakle ovdje se radi o skupu koji ima samo jedan član. Kad ti ti piše 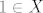 , to nije isto kao da piše , to nije isto kao da piše  , jer se u drugom slučaju radi o skupu, dok ovo prvo to nije. , jer se u drugom slučaju radi o skupu, dok ovo prvo to nije.
Ono što tebe sigurno zbunjuje, je zašto kod nekih familija podskupova nekog skupa(algebri, prstenova...) piše za neke skupove, npr. 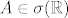
Nije precizna definicija, ali koristit ce, familije podskupova nekog skupa za svoje elemente imaju podskupove tog skupa. Uzmimo partitivni skup. Vrijedi ovo:
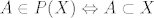
E sad, neka je npr.  familija podskupova od X. Tada familija podskupova od X. Tada  sadrži podskupove od X. Posebno, vrijedi sadrži podskupove od X. Posebno, vrijedi 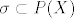 , ali ne vrijedi , ali ne vrijedi  . .
Nadam se da sam razjasnio 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 15:11 čet, 15. 3. 2012 Naslov: Postano: 15:11 čet, 15. 3. 2012 Naslov: |
    |
|
|
Dovoljno je dokazati da je [latex]\mathcal{R} \cup \mathcal{R}^c[/latex] prsten koji sadrži cijeli skup [latex]X[/latex]. Primijetimo da je za to dovoljno dokazati da je [latex]\mathcal{R} \cup \mathcal{R}^c[/latex] prsten pa onda, kako je [latex]\mathcal{R}[/latex] neprazna familija podkupova od [latex]X[/latex] postoji neki element [latex]A \in R[/latex], no tada je [latex]X = A \cup A^c[/latex] element od [latex]\mathcal{R} \cup \mathcal{R}^c[/latex], odnosno [latex]\mathcal{R} \cup \mathcal{R}^c[/latex] je algebra na [latex]X[/latex].
Trebamo dokazati da je familija [latex]\mathcal{R} \cup \mathcal{R}^c[/latex] zatvorena na operacije unije i razlike, s time da znamo da je familija [latex]\mathcal{R}[/latex] prsten.
Neka su [latex]A,\, B \in \mathcal{R} \cup \mathcal{R}^c[/latex], ukoliko su i [latex]A[/latex] i [latex]B[/latex] iz [latex]\mathcal{R}[/latex] sve trivijalno vrijedi jer je [latex]\mathcal{R}[/latex] prsten. Dakle, imamo dva (Točnije, tri, ali dva su potpuno analogna.) slučaja.
Ili je [latex]A \in \mathcal{R}[/latex] i [latex]B \in \mathcal{R}^c[/latex] (Isto kao i da je [latex]A \in \mathcal{R}^c[/latex] i [latex]B \in \mathcal{R}[/latex].) ili su [latex]A,\, B \in \mathcal{R}^c[/latex].
U prvom slučaju. Postoji [latex]C \in \mathcal{R}[/latex] takav da je [latex]B = C^c[/latex]. Tada je [latex]A \cup B = A \cup C^c = \left(A^c \cap C\right)^c = \left(C \setminus A\right)^c \in \mathcal{R}^c \subseteq \mathcal{R} \cup \mathcal{R}^c[/latex], jer je [latex]\mathcal{R}[/latex] prsten pa je [latex]C \setminus A \in \mathcal{R}[/latex].
Također [latex]A \setminus B = A \cap B^c = A \cap C \in \mathcal{R} \subseteq \mathcal{R} \cup \mathcal{R}^c[/latex]. [latex]A \cap C \in \mathcal{R}[/latex] zato što je [latex]\mathcal{R}[/latex] prsten.
U drugom slučaju, postoje [latex]C,\, D \in \mathcal{R}[/latex] takvi da je [latex]C^c = A[/latex] i [latex]D^c = B[/latex]. No, tada je
[latex]A \cup B = C^c \cup D^c = \left(C \cap D\right)^c \in \mathcal{R}^c \subseteq \mathcal{R} \cup \mathcal{R}^c[/latex]. Zato što je [latex]\mathcal{R}[/latex] prsten pa je [latex]C \cap D \in \mathcal{R}[/latex].
[latex]A \setminus B = A \cap B^c = C^c \cap D = D \setminus C \in \mathcal{R} \subseteq \mathcal{R} \cup \mathcal{R}^c[/latex].
Dakle, [latex]\mathcal{R} \cup \mathcal{R}^c[/latex] je prsten na [latex]X[/latex], a kao što smo na početku pokazali, to je tada algebra na [latex]X[/latex].
Dovoljno je dokazati da je 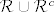 prsten koji sadrži cijeli skup prsten koji sadrži cijeli skup  . Primijetimo da je za to dovoljno dokazati da je . Primijetimo da je za to dovoljno dokazati da je 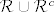 prsten pa onda, kako je prsten pa onda, kako je 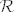 neprazna familija podkupova od neprazna familija podkupova od  postoji neki element postoji neki element 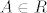 , no tada je , no tada je 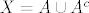 element od element od 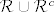 , odnosno , odnosno 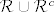 je algebra na je algebra na  . .
Trebamo dokazati da je familija 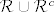 zatvorena na operacije unije i razlike, s time da znamo da je familija zatvorena na operacije unije i razlike, s time da znamo da je familija 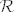 prsten. prsten.
Neka su  , ukoliko su i , ukoliko su i  i i  iz iz 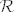 sve trivijalno vrijedi jer je sve trivijalno vrijedi jer je 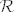 prsten. Dakle, imamo dva (Točnije, tri, ali dva su potpuno analogna.) slučaja. prsten. Dakle, imamo dva (Točnije, tri, ali dva su potpuno analogna.) slučaja.
Ili je 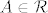 i i  (Isto kao i da je (Isto kao i da je  i i 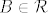 .) ili su .) ili su 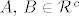 . .
U prvom slučaju. Postoji 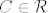 takav da je takav da je  . Tada je . Tada je 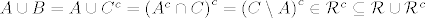 , jer je , jer je 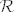 prsten pa je prsten pa je  . .
Također  . . 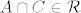 zato što je zato što je 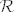 prsten. prsten.
U drugom slučaju, postoje 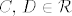 takvi da je takvi da je 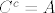 i i  . No, tada je . No, tada je
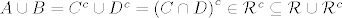 . Zato što je . Zato što je 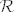 prsten pa je prsten pa je 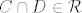 . .
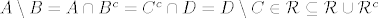 . .
Dakle, 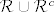 je prsten na je prsten na  , a kao što smo na početku pokazali, to je tada algebra na , a kao što smo na početku pokazali, to je tada algebra na  . .
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 17:11 čet, 5. 4. 2012 Naslov: Postano: 17:11 čet, 5. 4. 2012 Naslov: |
    |
|
|
Ako se dobro sjećam, samo na teoriji skupova smo pravili razliku između konačnih i prebrojivih skupova. Konačni su nam bili samo to, konačni (Dakle, među njima je i prazan skup, njegov kardinalitet je 0, što je konačno.)... :D Dok su nam prebrojivi bili oni koji su beskonačni i u bijekciji sa skupom prirodnih brojeva, [latex]\mathbb{N}[/latex].
Na mjeri se, opet napominjem, ako se dobro sjećam, podrazumijeva da su prebrojivi svi oni koji su ili konačni (Dakle i [latex]\emptyset[/latex].) ili prebrojivo beskonačni.
Ako se dobro sjećam, samo na teoriji skupova smo pravili razliku između konačnih i prebrojivih skupova. Konačni su nam bili samo to, konačni (Dakle, među njima je i prazan skup, njegov kardinalitet je 0, što je konačno.)...  Dok su nam prebrojivi bili oni koji su beskonačni i u bijekciji sa skupom prirodnih brojeva, Dok su nam prebrojivi bili oni koji su beskonačni i u bijekciji sa skupom prirodnih brojeva, 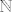 . .
Na mjeri se, opet napominjem, ako se dobro sjećam, podrazumijeva da su prebrojivi svi oni koji su ili konačni (Dakle i  .) ili prebrojivo beskonačni. .) ili prebrojivo beskonačni.
|
|
| [Vrh] |
|
xyz
Forumaš(ica)
Pridružen/a: 14. 02. 2009. (11:14:15)
Postovi: (8A)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 21:55 čet, 5. 4. 2012 Naslov: Postano: 21:55 čet, 5. 4. 2012 Naslov: |
    |
|
|
[quote="xyz"]Zar nije da za konacne skupove ne kazemo da su prebrojivi nego [i]najvise prebrojivi[/i]? :grebgreb:[/quote]
Termin [i]prebrojiv[/i] nije sasvim standardiziran u matematickoj literaturi, kao sto je kolega/ica JANKRI napomenuo/la. Zato se cesto zeli izbjeci nesporazum koristenjem termina poput "najvise prebrojiv", "prebrojivo beskonacan", itd.
Na kolegiju Mjera i integral [i]prebrojivim skupovima[/i] smatramo i konacne skupove i skupove koji su bijektivni s [tex]\mathbb{N}[/tex].
Takodjer, kao sto JANKRI rece, [tex]\emptyset[/tex] je konacan pa je specijalno i prebrojiv.
| xyz (napisa): | Zar nije da za konacne skupove ne kazemo da su prebrojivi nego najvise prebrojivi?  |
Termin prebrojiv nije sasvim standardiziran u matematickoj literaturi, kao sto je kolega/ica JANKRI napomenuo/la. Zato se cesto zeli izbjeci nesporazum koristenjem termina poput "najvise prebrojiv", "prebrojivo beskonacan", itd.
Na kolegiju Mjera i integral prebrojivim skupovima smatramo i konacne skupove i skupove koji su bijektivni s [tex]\mathbb{N}[/tex].
Takodjer, kao sto JANKRI rece, [tex]\emptyset[/tex] je konacan pa je specijalno i prebrojiv.
|
|
| [Vrh] |
|
Sphiro
Forumaš(ica)
Pridružen/a: 17. 10. 2007. (16:32:45)
Postovi: (45)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|













