| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 15:03 sub, 14. 4. 2012 Naslov: 1.kolokvij Postano: 15:03 sub, 14. 4. 2012 Naslov: 1.kolokvij |
    |
|
|
Može objašnjenje kako se rješava 4.zadatak od http://web.math.pmf.unizg.hr/~duje/utb/kol101a.pdf , ne dobivam jedno rješenje
dobije se da su [latex]p_i\in \{2,3,5\}[/latex], za 5 se dobi na ne može biti faktor od n,ostaju 2 i 3.
- za 3 se dobi da je n=3*k, k t.d. [latex]\varphi(k)=46[/latex], pa je k=47.
- za 2 sa potencijom 1 dobijem da je za n=2*k, [latex]\varphi(k)=92[/latex],ali je to ustvari zadatak,pa se vrtimo u krug
-za 2 s potencijom 2 se dobije da za n=4*k, k t.d. [latex]\varphi(k)=46[/latex], pa je k=47.
rješenja su 141,282,188, meni nedostaje 282. vidim da je to 2*141,ali ne znam kako do toga doći.
u istom kolokviju 5.b) dobivm krivo rješenje,a ne znam što krivo radim:
[latex](\frac{187}{523})=-(\frac{523}{187})=-(\frac{149}{187})=-(\frac{187-149}{187})=-(\frac{28}{187})=-(\frac{2}{187})(\frac{19}{187})=(\frac{19}{187})=-(\frac{187}{19})=-(\frac{16}{19})=-(\frac{2}{19})(\frac{2}{19})(\frac{2}{19})(\frac{2}{19})= -1[/latex]
i 4.zadatak odavde http://web.math.pmf.unizg.hr/~duje/utb/kol091a.pdf
dobila sam da je [latex]x \equiv 3,7,10 (mod 11) [/latex] i dobila sam one prve t-ove [latex]t=1,8,11[/latex] i dalje mi nije jasno što treba.
u 5.zadatku iz istog kolokvija ne dobivam točno rješenje, ne znam u čem je greška, jedino možda u indeksu, je li [latex]ind_{2} 35=36 mod 53 [/latex]?
Može objašnjenje kako se rješava 4.zadatak od http://web.math.pmf.unizg.hr/~duje/utb/kol101a.pdf , ne dobivam jedno rješenje
dobije se da su 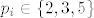 , za 5 se dobi na ne može biti faktor od n,ostaju 2 i 3. , za 5 se dobi na ne može biti faktor od n,ostaju 2 i 3.
- za 3 se dobi da je n=3*k, k t.d. 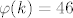 , pa je k=47. , pa je k=47.
- za 2 sa potencijom 1 dobijem da je za n=2*k, 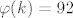 ,ali je to ustvari zadatak,pa se vrtimo u krug ,ali je to ustvari zadatak,pa se vrtimo u krug
-za 2 s potencijom 2 se dobije da za n=4*k, k t.d. 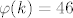 , pa je k=47. , pa je k=47.
rješenja su 141,282,188, meni nedostaje 282. vidim da je to 2*141,ali ne znam kako do toga doći.
u istom kolokviju 5.b) dobivm krivo rješenje,a ne znam što krivo radim:
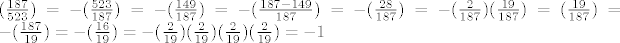
i 4.zadatak odavde http://web.math.pmf.unizg.hr/~duje/utb/kol091a.pdf
dobila sam da je 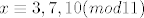 i dobila sam one prve t-ove i dobila sam one prve t-ove 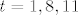 i dalje mi nije jasno što treba. i dalje mi nije jasno što treba.
u 5.zadatku iz istog kolokvija ne dobivam točno rješenje, ne znam u čem je greška, jedino možda u indeksu, je li 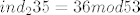 ? ?
|
|
| [Vrh] |
|
pravipurger
Forumaš(ica)


Pridružen/a: 11. 07. 2009. (10:29:44)
Postovi: (128)16
Spol: 
|
 Postano: 16:14 sub, 14. 4. 2012 Naslov: Re: 1.kolokvij Postano: 16:14 sub, 14. 4. 2012 Naslov: Re: 1.kolokvij |
    |
|
|
[quote=".anchy."]Može objašnjenje kako se rješava 4.zadatak od http://web.math.pmf.unizg.hr/~duje/utb/kol101a.pdf , ne dobivam jedno rješenje
dobije se da su [latex]p_i\in \{2,3,5\}[/latex], za 5 se dobi na ne može biti faktor od n,ostaju 2 i 3.
- za 3 se dobi da je n=3*k, k t.d. [latex]\varphi(k)=46[/latex], pa je k=47.
- za 2 sa potencijom 1 dobijem da je za n=2*k, [latex]\varphi(k)=92[/latex],ali je to ustvari zadatak,pa se vrtimo u krug
-za 2 s potencijom 2 se dobije da za n=4*k, k t.d. [latex]\varphi(k)=46[/latex], pa je k=47.
rješenja su 141,282,188, meni nedostaje 282. vidim da je to 2*141,ali ne znam kako do toga doći.
i 4.zadatak odavde http://web.math.pmf.unizg.hr/~duje/utb/kol091a.pdf
dobila sam da je [latex]x \equiv 3,7,10 (mod 11) [/latex] i dobila sam one prve t-ove [latex]t=1,8,11[/latex] i dalje mi nije jasno što treba.
u 5.zadatku iz istog kolokvija ne dobivam točno rješenje, ne znam u čem je greška, jedino možda u indeksu, je li [latex]ind_{2} 35=36 mod 53 [/latex]?[/quote]
1. p_i može biti i 47, iz njega se dobiju sva 3 rješenja.
4. u skripti imaš rješen zadatak sa drugim brojevima, za svaki dobiveni t računaš za a =3,t=1:
a'=a+t*11,
a'=3+11=14
sad ti je to a i opet uvrstiš u formulu
t'*f'(14)=-f(14)/11^2 (mod11)
rješiš kongruenciju, t'=3
a''=a'+t'*121=x=377(mod 11^3)
5. indeks je 9, pa to lako provjeriš 2^36 - 35 nije djeljivo s 53.
| .anchy. (napisa): | Može objašnjenje kako se rješava 4.zadatak od http://web.math.pmf.unizg.hr/~duje/utb/kol101a.pdf , ne dobivam jedno rješenje
dobije se da su 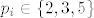 , za 5 se dobi na ne može biti faktor od n,ostaju 2 i 3. , za 5 se dobi na ne može biti faktor od n,ostaju 2 i 3.
- za 3 se dobi da je n=3*k, k t.d. 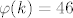 , pa je k=47. , pa je k=47.
- za 2 sa potencijom 1 dobijem da je za n=2*k, 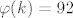 ,ali je to ustvari zadatak,pa se vrtimo u krug ,ali je to ustvari zadatak,pa se vrtimo u krug
-za 2 s potencijom 2 se dobije da za n=4*k, k t.d. 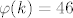 , pa je k=47. , pa je k=47.
rješenja su 141,282,188, meni nedostaje 282. vidim da je to 2*141,ali ne znam kako do toga doći.
i 4.zadatak odavde http://web.math.pmf.unizg.hr/~duje/utb/kol091a.pdf
dobila sam da je 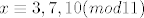 i dobila sam one prve t-ove i dobila sam one prve t-ove 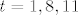 i dalje mi nije jasno što treba. i dalje mi nije jasno što treba.
u 5.zadatku iz istog kolokvija ne dobivam točno rješenje, ne znam u čem je greška, jedino možda u indeksu, je li 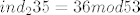 ? ? |
1. p_i može biti i 47, iz njega se dobiju sva 3 rješenja.
4. u skripti imaš rješen zadatak sa drugim brojevima, za svaki dobiveni t računaš za a =3,t=1:
a'=a+t*11,
a'=3+11=14
sad ti je to a i opet uvrstiš u formulu
t'*f'(14)=-f(14)/11^2 (mod11)
rješiš kongruenciju, t'=3
a''=a'+t'*121=x=377(mod 11^3)
5. indeks je 9, pa to lako provjeriš 2^36 - 35 nije djeljivo s 53.
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 18:28 sub, 14. 4. 2012 Naslov: Postano: 18:28 sub, 14. 4. 2012 Naslov: |
    |
|
|
Hvala ti..
Zapela sam na 4.zadatku iz 2008., odrediti fi( 8 )..
pi su {2,3,5}
-n=5*k, dobivam k=3,4,6
dakle,neka od rješenja su 15,20,30
-n=3*k
treba biti fi(k)=4;to sam išla rješavati, pi su iz {2,3,5}
za k=5*k' dobim k'=1 ili 2
za k'=3*k dobim da fi(k')=2, a to vrijedi za k'=3,4,6 , ali to nisu rješenja.Ne znam zašto tako ispada..
i što na kraju sa n=2*k, dobivam fi(k)=8, i opet smo na početku.
ne razumijem baš rješavanje tih zadataka :?
Hvala ti..
Zapela sam na 4.zadatku iz 2008., odrediti fi( 8 )..
pi su {2,3,5}
-n=5*k, dobivam k=3,4,6
dakle,neka od rješenja su 15,20,30
-n=3*k
treba biti fi(k)=4;to sam išla rješavati, pi su iz {2,3,5}
za k=5*k' dobim k'=1 ili 2
za k'=3*k dobim da fi(k')=2, a to vrijedi za k'=3,4,6 , ali to nisu rješenja.Ne znam zašto tako ispada..
i što na kraju sa n=2*k, dobivam fi(k)=8, i opet smo na početku.
ne razumijem baš rješavanje tih zadataka 
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
 Postano: 19:23 sub, 14. 4. 2012 Naslov: Re: 1.kolokvij Postano: 19:23 sub, 14. 4. 2012 Naslov: Re: 1.kolokvij |
    |
|
|
[quote=".anchy."]
odrediti fi(n)=8
pi su {2,3,5}
-n=5*k, dobivam k=3,4,6
dakle,neka od rješenja su 15,20,30
-n=3*k
treba biti fi(k)=4;to sam išla rješavati, pi su iz {2,3,5}
[/quote]
Dodatni uvjeti su da k nije djeljiv sa 5 (jer je rijeseno u prethodnom koraku), a nije ni djeljiv sa 3 (3 i k moraju biti relativno prosti da bi se
primjenila multiplikativnost). Zato je k=2^a. Pa se dobije 2^(a-1)=4, tj. a=3, k=8 i n=24.
[quote=".anchy."]
i što na kraju sa n=2*k,
[/quote]
Nakon što ste riješili slučajeve kada je n djeljiv sa 5 i 3, ostaje slučaj da je n djeljiv samo sa 2, a to nije 2*k, nego 2^a. Pa iz 2^(a-1)=8 slijedi a=4 i n=16.
Dakle, sva rješenja su n=15,16,20,24,30.
[size=9][color=#999999]Added after 5 minutes:[/color][/size]
[quote=".anchy."]
ne znam što krivo radim:
[latex](\frac{187}{523})=-(\frac{523}{187})=-(\frac{149}{187})=-(\frac{187-149}{187})=-(\frac{28}{187})=-(\frac{2}{187})(\frac{19}{187})=(\frac{19}{187})=-(\frac{187}{19})=-(\frac{16}{19})=-(\frac{2}{19})(\frac{2}{19})(\frac{2}{19})(\frac{2}{19})= -1[/latex]
[/quote]
Krivo je ovo:
[latex]-(\frac{149}{187})=-(\frac{187-149}{187})[/latex]
| .anchy. (napisa): |
odrediti fi(n)=8
pi su {2,3,5}
-n=5*k, dobivam k=3,4,6
dakle,neka od rješenja su 15,20,30
-n=3*k
treba biti fi(k)=4;to sam išla rješavati, pi su iz {2,3,5}
|
Dodatni uvjeti su da k nije djeljiv sa 5 (jer je rijeseno u prethodnom koraku), a nije ni djeljiv sa 3 (3 i k moraju biti relativno prosti da bi se
primjenila multiplikativnost). Zato je k=2^a. Pa se dobije 2^(a-1)=4, tj. a=3, k=8 i n=24.
| .anchy. (napisa): |
i što na kraju sa n=2*k,
|
Nakon što ste riješili slučajeve kada je n djeljiv sa 5 i 3, ostaje slučaj da je n djeljiv samo sa 2, a to nije 2*k, nego 2^a. Pa iz 2^(a-1)=8 slijedi a=4 i n=16.
Dakle, sva rješenja su n=15,16,20,24,30.
Added after 5 minutes:
| .anchy. (napisa): |
ne znam što krivo radim:
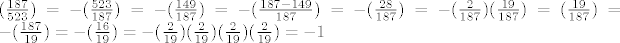
|
Krivo je ovo:
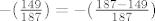
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
:D
Gost
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
 Postano: 10:54 ned, 15. 4. 2012 Naslov: Postano: 10:54 ned, 15. 4. 2012 Naslov: |
    |
|
|
[quote]2. zadatak tipa primjer 2.5 u skripti gdje se odreduju zadnje dvije znamenke, jel moze netko objasniti sto se tu tocno radi, jer ne kuzim bas ovo rjesenje iz skripte[/quote]
Odrediti zadnje dvije znamenke nekog prirodnog broja znači naći njegov ostatak pri dijeljenju sa 100. A to se kod brojeva oblika ako što onaj iz tog primjera može tako da se primjenom Eulevog teorema nađe ostatak pri dijeljenju sa 4 i 25, pa se konačni rezultat modulo 100 dobije iz općenito iz Kineskog teorema o ostacima (a ako ispadne isti ostatak pri dijeljenju sa 4 i sa 25, onda je to i ostatak pri dijeljenje sa 100).
[size=9][color=#999999]Added after 5 minutes:[/color][/size]
[quote]otkud u zadatku phi(n)=42 dobijemo rjesenja 49 i 98. [/quote]
Jedan od slučajeva koji treba razmotriti je kad je n djeljiv sa 7.
Tu postoje dvije mogućnosti:
1) n=7*k, gdje k nije djeljiv sa 7. Tu se dobije 42=phi(n)=6*phi(k), tj. phi(k)=7, što nema rješenja jer phi(k) ne može biti neparan broj veći od 1.
2) n=7^2*k, gdje k nije djeljiv sa 7. Tu se dobije 42=phi(n)=7*6*phi(1), tj. phi(k)=1, pa je k=1,2, tj. n=49, 98.
| Citat: | | 2. zadatak tipa primjer 2.5 u skripti gdje se odreduju zadnje dvije znamenke, jel moze netko objasniti sto se tu tocno radi, jer ne kuzim bas ovo rjesenje iz skripte |
Odrediti zadnje dvije znamenke nekog prirodnog broja znači naći njegov ostatak pri dijeljenju sa 100. A to se kod brojeva oblika ako što onaj iz tog primjera može tako da se primjenom Eulevog teorema nađe ostatak pri dijeljenju sa 4 i 25, pa se konačni rezultat modulo 100 dobije iz općenito iz Kineskog teorema o ostacima (a ako ispadne isti ostatak pri dijeljenju sa 4 i sa 25, onda je to i ostatak pri dijeljenje sa 100).
Added after 5 minutes:
| Citat: | | otkud u zadatku phi(n)=42 dobijemo rjesenja 49 i 98. |
Jedan od slučajeva koji treba razmotriti je kad je n djeljiv sa 7.
Tu postoje dvije mogućnosti:
1) n=7*k, gdje k nije djeljiv sa 7. Tu se dobije 42=phi(n)=6*phi(k), tj. phi(k)=7, što nema rješenja jer phi(k) ne može biti neparan broj veći od 1.
2) n=7^2*k, gdje k nije djeljiv sa 7. Tu se dobije 42=phi(n)=7*6*phi(1), tj. phi(k)=1, pa je k=1,2, tj. n=49, 98.
|
|
| [Vrh] |
|
:D
Gost
|
 Postano: 11:08 ned, 15. 4. 2012 Naslov: Postano: 11:08 ned, 15. 4. 2012 Naslov: |
    |
|
|
[quote] Jedan od slučajeva koji treba razmotriti je kad je n djeljiv sa 7.
Tu postoje dvije mogućnosti:
1) n=7*k, gdje k nije djeljiv sa 7. Tu se dobije 42=phi(n)=6*phi(k), tj. phi(k)=7, što nema rješenja jer phi(k) ne može biti neparan broj veći od 1.
2) n=7^2*k, gdje k nije djeljiv sa 7. Tu se dobije 42=phi(n)=7*6*phi(1), tj. phi(k)=1, pa je k=1,2, tj. n=49, 98.[/quote]
A zasto u ovom zadatku imamo jos n=7^2*k?
Mislim, uvijek smo promatrali n oblika 5*k, 7*k, ... n=k
| Citat: | Jedan od slučajeva koji treba razmotriti je kad je n djeljiv sa 7.
Tu postoje dvije mogućnosti:
1) n=7*k, gdje k nije djeljiv sa 7. Tu se dobije 42=phi(n)=6*phi(k), tj. phi(k)=7, što nema rješenja jer phi(k) ne može biti neparan broj veći od 1.
2) n=7^2*k, gdje k nije djeljiv sa 7. Tu se dobije 42=phi(n)=7*6*phi(1), tj. phi(k)=1, pa je k=1,2, tj. n=49, 98. |
A zasto u ovom zadatku imamo jos n=7^2*k?
Mislim, uvijek smo promatrali n oblika 5*k, 7*k, ... n=k
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
 Postano: 11:19 ned, 15. 4. 2012 Naslov: Postano: 11:19 ned, 15. 4. 2012 Naslov: |
    |
|
|
[quote]A zasto u ovom zadatku imamo jos n=7^2*k?
Mislim, uvijek smo promatrali n oblika 5*k, 7*k, ... n=k[/quote]
Zato sto je 42 djeljivo ne samo za phi(7) (zato uopce gledamo 7),
nego i sa phi(7^2)=42.
Kod brojeva koji su djeljivi sa phi(5^2)=20, trebalo bi gledati i slučaj n=5^2*k, kod brojeva djeljivih sa phi(5^3)=100 i slučaj n=5^3*k, itd.
| Citat: | A zasto u ovom zadatku imamo jos n=7^2*k?
Mislim, uvijek smo promatrali n oblika 5*k, 7*k, ... n=k |
Zato sto je 42 djeljivo ne samo za phi(7) (zato uopce gledamo 7),
nego i sa phi(7^2)=42.
Kod brojeva koji su djeljivi sa phi(5^2)=20, trebalo bi gledati i slučaj n=5^2*k, kod brojeva djeljivih sa phi(5^3)=100 i slučaj n=5^3*k, itd.
Zadnja promjena: duje; 11:25 ned, 15. 4. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Gost
|
 Postano: 11:25 ned, 15. 4. 2012 Naslov: Postano: 11:25 ned, 15. 4. 2012 Naslov: |
    |
|
|
[quote="duje"][quote]A zasto u ovom zadatku imamo jos n=7^2*k?
Mislim, uvijek smo promatrali n oblika 5*k, 7*k, ... n=k[/quote]
Zato sto je 42 djeljivo ne samo za phi(7) (zato uopce gledamo 7),
nego i sa phi(7^2)=42.
Kod brojeva koji su djeljivi sa phi(5^2)=20, trebalo bi gledati i slučaj n=5^2*k, kod brojeva djeljivih sa phi(5^3)=80 i slučaj n=5^3*k, itd.[/quote]
Aha, kuzim sad. Hvala puno na pomoci :D
| duje (napisa): | | Citat: | A zasto u ovom zadatku imamo jos n=7^2*k?
Mislim, uvijek smo promatrali n oblika 5*k, 7*k, ... n=k |
Zato sto je 42 djeljivo ne samo za phi(7) (zato uopce gledamo 7),
nego i sa phi(7^2)=42.
Kod brojeva koji su djeljivi sa phi(5^2)=20, trebalo bi gledati i slučaj n=5^2*k, kod brojeva djeljivih sa phi(5^3)=80 i slučaj n=5^3*k, itd. |
Aha, kuzim sad. Hvala puno na pomoci 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
 Postano: 12:00 ned, 15. 4. 2012 Naslov: Re: 1.kolokvij Postano: 12:00 ned, 15. 4. 2012 Naslov: Re: 1.kolokvij |
    |
|
|
[quote="pedro"][quote=".anchy."]
i 4.zadatak odavde http://web.math.pmf.unizg.hr/~duje/utb/kol091a.pdf
dobila sam da je [latex]x \equiv 3,7,10 (mod 11) [/latex]
[/quote]
kako se dobiju ta rješenja???[/quote]
Uvrsti se x=0,1,2,3,4,5,6,7,8,9,10, pa se vidi za koji je od tih brojeva broj x^3 + 2x^2 +10 djeljiv s 11. Budući da je polinom 3. stupnja, a broj 11 prost, kongruencija ima najviše 3 rješenja modulo 11.
| pedro (napisa): |
kako se dobiju ta rješenja??? |
Uvrsti se x=0,1,2,3,4,5,6,7,8,9,10, pa se vidi za koji je od tih brojeva broj x^3 + 2x^2 +10 djeljiv s 11. Budući da je polinom 3. stupnja, a broj 11 prost, kongruencija ima najviše 3 rješenja modulo 11.
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
 Postano: 13:30 ned, 15. 4. 2012 Naslov: Re: 1.kolokvij Postano: 13:30 ned, 15. 4. 2012 Naslov: Re: 1.kolokvij |
    |
|
|
[quote="pravipurger"][quote=".anchy."]Može objašnjenje kako se rješava 4.zadatak od http://web.math.pmf.unizg.hr/~duje/utb/kol101a.pdf , ne dobivam jedno rješenje
dobije se da su [latex]p_i\in \{2,3,5\}[/latex], za 5 se dobi na ne može biti faktor od n,ostaju 2 i 3.
- za 3 se dobi da je n=3*k, k t.d. [latex]\varphi(k)=46[/latex], pa je k=47.
- za 2 sa potencijom 1 dobijem da je za n=2*k, [latex]\varphi(k)=92[/latex],ali je to ustvari zadatak,pa se vrtimo u krug
-za 2 s potencijom 2 se dobije da za n=4*k, k t.d. [latex]\varphi(k)=46[/latex], pa je k=47.
rješenja su 141,282,188, meni nedostaje 282. vidim da je to 2*141,ali ne znam kako do toga doći.
i 4.zadatak odavde http://web.math.pmf.unizg.hr/~duje/utb/kol091a.pdf
dobila sam da je [latex]x \equiv 3,7,10 (mod 11) [/latex] i dobila sam one prve t-ove [latex]t=1,8,11[/latex] i dalje mi nije jasno što treba.
u 5.zadatku iz istog kolokvija ne dobivam točno rješenje, ne znam u čem je greška, jedino možda u indeksu, je li [latex]ind_{2} 35=36 mod 53 [/latex]?[/quote]
1. p_i može biti i 47, iz njega se dobiju sva 3 rješenja.[/quote]
Možeš li napisati kako iz toga dobiješ 282 jer ga ni ja ne mogu dobiti. Hvala :D
| pravipurger (napisa): | | .anchy. (napisa): | Može objašnjenje kako se rješava 4.zadatak od http://web.math.pmf.unizg.hr/~duje/utb/kol101a.pdf , ne dobivam jedno rješenje
dobije se da su 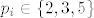 , za 5 se dobi na ne može biti faktor od n,ostaju 2 i 3. , za 5 se dobi na ne može biti faktor od n,ostaju 2 i 3.
- za 3 se dobi da je n=3*k, k t.d. 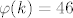 , pa je k=47. , pa je k=47.
- za 2 sa potencijom 1 dobijem da je za n=2*k, 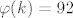 ,ali je to ustvari zadatak,pa se vrtimo u krug ,ali je to ustvari zadatak,pa se vrtimo u krug
-za 2 s potencijom 2 se dobije da za n=4*k, k t.d. 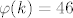 , pa je k=47. , pa je k=47.
rješenja su 141,282,188, meni nedostaje 282. vidim da je to 2*141,ali ne znam kako do toga doći.
i 4.zadatak odavde http://web.math.pmf.unizg.hr/~duje/utb/kol091a.pdf
dobila sam da je 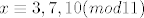 i dobila sam one prve t-ove i dobila sam one prve t-ove 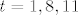 i dalje mi nije jasno što treba. i dalje mi nije jasno što treba.
u 5.zadatku iz istog kolokvija ne dobivam točno rješenje, ne znam u čem je greška, jedino možda u indeksu, je li 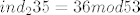 ? ? |
1. p_i može biti i 47, iz njega se dobiju sva 3 rješenja. |
Možeš li napisati kako iz toga dobiješ 282 jer ga ni ja ne mogu dobiti. Hvala 
|
|
| [Vrh] |
|
Gost
|
 Postano: 13:40 ned, 15. 4. 2012 Naslov: Re: 1.kolokvij Postano: 13:40 ned, 15. 4. 2012 Naslov: Re: 1.kolokvij |
    |
|
|
[quote="suza"]
Možeš li napisati kako iz toga dobiješ 282 jer ga ni ja ne mogu dobiti. Hvala :D[/quote]
n=47*k -> phi(n)=46*phi(k), sto znaci da mora biti phi(k) = 2 a to vrijedi za k=3,4,6 iz cega dobijemo da je n=141,188,282
| suza (napisa): |
Možeš li napisati kako iz toga dobiješ 282 jer ga ni ja ne mogu dobiti. Hvala  |
n=47*k → phi(n)=46*phi(k), sto znaci da mora biti phi(k) = 2 a to vrijedi za k=3,4,6 iz cega dobijemo da je n=141,188,282
|
|
| [Vrh] |
|
|











