| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 17:03 uto, 9. 11. 2004 Naslov: Kantor i paradoxi u teoriji skupova Postano: 17:03 uto, 9. 11. 2004 Naslov: Kantor i paradoxi u teoriji skupova |
    |
|
|
eto...mene to vec duze vrijeme muci. naime, od jednog kolege sa 3. godine sam saznao za neke paradoxe koje si bas i ne mogu predociti niti ih mogu shvatiti. o cemu se radi?!
Kantor je prije nekih 150 godina postavio jedan problem ovako:
zamislimo hotel sa beskonacno mnogo soba. sada zamislimo beskonacno takvih hotela. to je prebrojiv skup.
dakle...mene interesira, kako to moze biti prebrojiv skup ako smo ga vec definirali kao beskonacnog?! ako zamislimo da su ti hoteli jedan skup, jedino sto mi pada na pamet jest konstruiranje bijekcije sa tog skupa na skup N. ako postoji, onda je taj skup prebrojiv. medjutim, meni to nikako ne ide.
osim toga, imam jos jedno pitanje (iako bi ono vise spadalo pod elementarnu). kakav je to skup koji nije element samog sebe?! ako gledamo logicki, takav skup ne postoji jer svaki skup sadrzi barem jedan element, samog sebe. kako je moguce matematicki definirati pojam koji je u suprotnosti sa zdravom logikom?!
nadalje, tu se postavlja i pitanje: sto je to prazan skup?! ako definiramo prazan skup kao skup koji ima nista elemenata, onda znaci da taj skup ipak nije prazan, odnosno, on sadrzi jedan element, nista. a ako je nista element, onda je [b]nista[/b] [i]nesto[/i]...a to je nemoguce jer nesto sto ne postoji ne moze biti definirano kao nekakav element. molio bih vas da mi to objasnite. zahvaljujem se na aznji.
eto...mene to vec duze vrijeme muci. naime, od jednog kolege sa 3. godine sam saznao za neke paradoxe koje si bas i ne mogu predociti niti ih mogu shvatiti. o cemu se radi?!
Kantor je prije nekih 150 godina postavio jedan problem ovako:
zamislimo hotel sa beskonacno mnogo soba. sada zamislimo beskonacno takvih hotela. to je prebrojiv skup.
dakle...mene interesira, kako to moze biti prebrojiv skup ako smo ga vec definirali kao beskonacnog?! ako zamislimo da su ti hoteli jedan skup, jedino sto mi pada na pamet jest konstruiranje bijekcije sa tog skupa na skup N. ako postoji, onda je taj skup prebrojiv. medjutim, meni to nikako ne ide.
osim toga, imam jos jedno pitanje (iako bi ono vise spadalo pod elementarnu). kakav je to skup koji nije element samog sebe?! ako gledamo logicki, takav skup ne postoji jer svaki skup sadrzi barem jedan element, samog sebe. kako je moguce matematicki definirati pojam koji je u suprotnosti sa zdravom logikom?!
nadalje, tu se postavlja i pitanje: sto je to prazan skup?! ako definiramo prazan skup kao skup koji ima nista elemenata, onda znaci da taj skup ipak nije prazan, odnosno, on sadrzi jedan element, nista. a ako je nista element, onda je nista nesto...a to je nemoguce jer nesto sto ne postoji ne moze biti definirano kao nekakav element. molio bih vas da mi to objasnite. zahvaljujem se na aznji.
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 17:53 uto, 9. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova Postano: 17:53 uto, 9. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova |
    |
|
|
[quote="HijenA"]
Kantor je prije nekih 150 godina postavio jedan problem ovako:
zamislimo hotel sa beskonacno mnogo soba. sada zamislimo beskonacno takvih hotela. to je prebrojiv skup.
dakle...mene interesira, kako to moze biti prebrojiv skup ako smo ga vec definirali kao beskonacnog?! ako zamislimo da su ti hoteli jedan skup, jedino sto mi pada na pamet jest konstruiranje bijekcije sa tog skupa na skup N. ako postoji, onda je taj skup prebrojiv. medjutim, meni to nikako ne ide.
[/quote]
Oznacimo sa (i, j) j-tu sobu u i-tom hotelu. Sada imas nesto sto se moze opisati kao beskonacna matrica:
(1,1) (1,2) (1,3).....
(2,1) (2,2) (2,3).....
(3,1) (3,2) (3,3).....
....
....
....
OK, sada kupi sve te uredjene parove po 'dijagonalama', ovako:
(1,1), (1,2), (2,1), (1,3), (2,2), (3,1), ....
Odnosno, prvo pokupi sve kojima je zbroj koordinata 2, nakon toga 3, pa 4 itd. Ocito je da se uz mrvicu truda moze napisati i formula koja ostvaruje bijektivno preslikavanje izmedju |N x |N i |N.
[quote]kakav je to skup koji nije element samog sebe?! ako gledamo logicki, takav skup ne postoji jer svaki skup sadrzi barem jedan element, samog sebe. kako je moguce matematicki definirati pojam koji je u suprotnosti sa zdravom logikom?![/quote]
:blueshock: :blueshock: :blueshock: :blueshock: :blueshock:
Kod Russelovog paradoksa upravo i jeste problem u tome sto nijedan skup ne moze sadrzavati samog sebe! (konkretno u ZF teoriji to je u suprotnosti s aksiomom utemeljenosti)
Usput, jesi li se ikada zapitao sto je to zdrava logika?
[quote]nadalje, tu se postavlja i pitanje: sto je to prazan skup?! ako definiramo prazan skup kao skup koji ima nista elemenata, onda znaci da taj skup ipak nije prazan, odnosno, on sadrzi jedan element, nista. a ako je nista element, onda je [b]nista[/b] [i]nesto[/i]...a to je nemoguce jer nesto sto ne postoji ne moze biti definirano kao nekakav element. molio bih vas da mi to objasnite. zahvaljujem se na aznji.[/quote]
Prazan skup je upravo skup bez elemenata. Ako ti pomaze zamisljaj ga kao {x | x != x} jer mi se cini da je formalna definicija preslozena za ovaj topic.
Vezano za prazan skup vec postoji jedan topic [url]http://degiorgi.math.hr/forum/viewtopic.php?t=2888[/url]
| HijenA (napisa): |
Kantor je prije nekih 150 godina postavio jedan problem ovako:
zamislimo hotel sa beskonacno mnogo soba. sada zamislimo beskonacno takvih hotela. to je prebrojiv skup.
dakle...mene interesira, kako to moze biti prebrojiv skup ako smo ga vec definirali kao beskonacnog?! ako zamislimo da su ti hoteli jedan skup, jedino sto mi pada na pamet jest konstruiranje bijekcije sa tog skupa na skup N. ako postoji, onda je taj skup prebrojiv. medjutim, meni to nikako ne ide.
|
Oznacimo sa (i, j) j-tu sobu u i-tom hotelu. Sada imas nesto sto se moze opisati kao beskonacna matrica:
(1,1) (1,2) (1,3).....
(2,1) (2,2) (2,3).....
(3,1) (3,2) (3,3).....
....
....
....
OK, sada kupi sve te uredjene parove po 'dijagonalama', ovako:
(1,1), (1,2), (2,1), (1,3), (2,2), (3,1), ....
Odnosno, prvo pokupi sve kojima je zbroj koordinata 2, nakon toga 3, pa 4 itd. Ocito je da se uz mrvicu truda moze napisati i formula koja ostvaruje bijektivno preslikavanje izmedju |N x |N i |N.
| Citat: | | kakav je to skup koji nije element samog sebe?! ako gledamo logicki, takav skup ne postoji jer svaki skup sadrzi barem jedan element, samog sebe. kako je moguce matematicki definirati pojam koji je u suprotnosti sa zdravom logikom?! |
    
Kod Russelovog paradoksa upravo i jeste problem u tome sto nijedan skup ne moze sadrzavati samog sebe! (konkretno u ZF teoriji to je u suprotnosti s aksiomom utemeljenosti)
Usput, jesi li se ikada zapitao sto je to zdrava logika?
| Citat: | | nadalje, tu se postavlja i pitanje: sto je to prazan skup?! ako definiramo prazan skup kao skup koji ima nista elemenata, onda znaci da taj skup ipak nije prazan, odnosno, on sadrzi jedan element, nista. a ako je nista element, onda je nista nesto...a to je nemoguce jer nesto sto ne postoji ne moze biti definirano kao nekakav element. molio bih vas da mi to objasnite. zahvaljujem se na aznji. |
Prazan skup je upravo skup bez elemenata. Ako ti pomaze zamisljaj ga kao {x | x != x} jer mi se cini da je formalna definicija preslozena za ovaj topic.
Vezano za prazan skup vec postoji jedan topic http://degiorgi.math.hr/forum/viewtopic.php?t=2888
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 18:55 uto, 9. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova Postano: 18:55 uto, 9. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova |
    |
|
|
[quote="HijenA"]eto...mene to vec duze vrijeme muci.[/quote]
Pa što nisi pitao prije? :-)
[quote]Kantor je prije nekih 150 godina postavio jedan problem ovako:
zamislimo hotel sa beskonacno mnogo soba. sada zamislimo beskonacno takvih hotela. to je prebrojiv skup.[/quote]
_Što točno_ (je prebrojiv skup)? Pretpostavljam da _hotelâ_ ima (beskonačno) prebrojivo mnogo, i da _svaki_ od tih hotelâ ima (beskonačno) prebrojivo mnogo sobâ.
[quote]dakle...mene interesira, kako to moze biti prebrojiv skup ako smo ga vec definirali kao beskonacnog?![/quote]
_Koje_? Trenutno imaš hrpu skupova u igri, od kojih si neke definirao kao beskonačne. Konkretno, imaš skup hotelâ, H , i za svaki hotel h@H , imaš skup njegovih sobâ s_h . Naravno, osim svega toga, imaš i skup _svih_ soba u svim tim hotelima, S , što je zapravo S:=U_h@H s_h (unija svih s_h , po h iz H ). Ti si definirao da je skup H beskonačan, i da je za svaki h@H , skup s_h beskonačan.
Ako je točna ona moja pretpostavka gore napisana, tada si rekao i više: da su skup H , i svi skupovi s_h , beskonačno _prebrojivi_, tj. bijektivni sa skupom \N .
[quote] ako zamislimo da su ti hoteli jedan skup, jedino sto mi pada na pamet jest konstruiranje bijekcije sa tog skupa na skup N. ako postoji, onda je taj skup prebrojiv. medjutim, meni to nikako ne ide.[/quote]
To je pak trivijalno. Pretpostavka zadatka je da je H prebrojivo beskonačan. Ono što je malo manje trivijalno, jest da je i S prebrojivo beskonačan. A to je ono što je mdoko gore "dokazao" (do na onu "mrvicu truda", što ću ja popraviti: s f(i,j):=((i+j-1)povrh2)+i je zadana bijekcija između |Nx|N i |N ).
[quote]osim toga, imam jos jedno pitanje (iako bi ono vise spadalo pod elementarnu). kakav je to skup koji nije element samog sebe?![/quote]
Recimo, prazan skup je takav. Ništa nije element praznog skupa, pa tako ni on sam.
Recimo, skup {1,2,3} je takav. Broj 1 je njegov element. Broj 2 je njegov element. Broj 3 je njegov element. No bilo što drugo, različito od brojeva 1 , 2 i 3 , _nije_ njegov element. Specijalno, skup {1,2,3} je različit i od broja 1 i od broja 2 i od broja 3 (i ovo se može dokazati, no uzmimo intuitivno da je to jasno), te on nije element skupa {1,2,3} , odnosno samog sebe.
Primijeti, on _jest_ svoj _podskup_, kao što je svaki skup podskup samog sebe. Ali nije svoj _element_ - štoviše, u ZF , standardnoj teoriji skupova, nijedan skup nije element samog sebe.
[quote] ako gledamo logicki, takav skup ne postoji jer svaki skup sadrzi barem jedan element, samog sebe.[/quote]
Njet. Vjerojatno želiš zamijeniti riješ "element" rječju "podskup".
Vidi http://degiorgi.math.hr/forum/viewtopic.php?p=20454#20454 za dalje (ako ti se ne da sve čitati, traži (unutar citata) "on sadrži i ništa").
[quote] kako je moguce matematicki definirati pojam koji je u suprotnosti sa zdravom logikom?! [/quote]
Easy. Pogledaj npr. Peanovu krivulju. ;-)
http://www.cut-the-knot.org/do_you_know/hilbert.shtml
[quote]nadalje, tu se postavlja i pitanje: sto je to prazan skup?![/quote]
To je skup koji nema elemenata. Preciznije, to je skup 0 takav da za svaki x vrijedi !(x@0) (nije x element od 0 ).
[quote] ako definiramo prazan skup kao skup koji ima nista elemenata, onda znaci da taj skup ipak nije prazan, odnosno, on sadrzi jedan element, nista.[/quote]
Wrong. U onom linku koji sam ti dao, odskrolaj koji ekran gore, do onog "No cat has eight tails.". Ovo je jezička pogreška.
[quote] a ako je nista element, onda je [b]nista[/b] [i]nesto[/i]...a to je nemoguce jer nesto sto ne postoji ne moze biti definirano kao nekakav element.[/quote]
Slažem se. I zato
1) "Ništa" nije matematički pojam
2) prazan skup se ne definira pomoću "ništa", već na gornji način.
HTH,
| HijenA (napisa): | | eto...mene to vec duze vrijeme muci. |
Pa što nisi pitao prije? 
| Citat: | Kantor je prije nekih 150 godina postavio jedan problem ovako:
zamislimo hotel sa beskonacno mnogo soba. sada zamislimo beskonacno takvih hotela. to je prebrojiv skup. |
_Što točno_ (je prebrojiv skup)? Pretpostavljam da _hotelâ_ ima (beskonačno) prebrojivo mnogo, i da _svaki_ od tih hotelâ ima (beskonačno) prebrojivo mnogo sobâ.
| Citat: | | dakle...mene interesira, kako to moze biti prebrojiv skup ako smo ga vec definirali kao beskonacnog?! |
_Koje_? Trenutno imaš hrpu skupova u igri, od kojih si neke definirao kao beskonačne. Konkretno, imaš skup hotelâ, H , i za svaki hotel h@H , imaš skup njegovih sobâ s_h . Naravno, osim svega toga, imaš i skup _svih_ soba u svim tim hotelima, S , što je zapravo S:=U_h@H s_h (unija svih s_h , po h iz H ). Ti si definirao da je skup H beskonačan, i da je za svaki h@H , skup s_h beskonačan.
Ako je točna ona moja pretpostavka gore napisana, tada si rekao i više: da su skup H , i svi skupovi s_h , beskonačno _prebrojivi_, tj. bijektivni sa skupom \N .
| Citat: | | ako zamislimo da su ti hoteli jedan skup, jedino sto mi pada na pamet jest konstruiranje bijekcije sa tog skupa na skup N. ako postoji, onda je taj skup prebrojiv. medjutim, meni to nikako ne ide. |
To je pak trivijalno. Pretpostavka zadatka je da je H prebrojivo beskonačan. Ono što je malo manje trivijalno, jest da je i S prebrojivo beskonačan. A to je ono što je mdoko gore "dokazao" (do na onu "mrvicu truda", što ću ja popraviti: s f(i,j):=((i+j-1)povrh2)+i je zadana bijekcija između |Nx|N i |N ).
| Citat: | | osim toga, imam jos jedno pitanje (iako bi ono vise spadalo pod elementarnu). kakav je to skup koji nije element samog sebe?! |
Recimo, prazan skup je takav. Ništa nije element praznog skupa, pa tako ni on sam.
Recimo, skup {1,2,3} je takav. Broj 1 je njegov element. Broj 2 je njegov element. Broj 3 je njegov element. No bilo što drugo, različito od brojeva 1 , 2 i 3 , _nije_ njegov element. Specijalno, skup {1,2,3} je različit i od broja 1 i od broja 2 i od broja 3 (i ovo se može dokazati, no uzmimo intuitivno da je to jasno), te on nije element skupa {1,2,3} , odnosno samog sebe.
Primijeti, on _jest_ svoj _podskup_, kao što je svaki skup podskup samog sebe. Ali nije svoj _element_ - štoviše, u ZF , standardnoj teoriji skupova, nijedan skup nije element samog sebe.
| Citat: | | ako gledamo logicki, takav skup ne postoji jer svaki skup sadrzi barem jedan element, samog sebe. |
Njet. Vjerojatno želiš zamijeniti riješ "element" rječju "podskup".
Vidi http://degiorgi.math.hr/forum/viewtopic.php?p=20454#20454 za dalje (ako ti se ne da sve čitati, traži (unutar citata) "on sadrži i ništa").
| Citat: | | kako je moguce matematicki definirati pojam koji je u suprotnosti sa zdravom logikom?! |
Easy. Pogledaj npr. Peanovu krivulju. 
http://www.cut-the-knot.org/do_you_know/hilbert.shtml
| Citat: | | nadalje, tu se postavlja i pitanje: sto je to prazan skup?! |
To je skup koji nema elemenata. Preciznije, to je skup 0 takav da za svaki x vrijedi !(x@0) (nije x element od 0 ).
| Citat: | | ako definiramo prazan skup kao skup koji ima nista elemenata, onda znaci da taj skup ipak nije prazan, odnosno, on sadrzi jedan element, nista. |
Wrong. U onom linku koji sam ti dao, odskrolaj koji ekran gore, do onog "No cat has eight tails.". Ovo je jezička pogreška.
| Citat: | | a ako je nista element, onda je nista nesto...a to je nemoguce jer nesto sto ne postoji ne moze biti definirano kao nekakav element. |
Slažem se. I zato
1) "Ništa" nije matematički pojam
2) prazan skup se ne definira pomoću "ništa", već na gornji način.
HTH,
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 20:10 uto, 9. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova Postano: 20:10 uto, 9. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova |
    |
|
|
[quote="mdoko"][quote="HijenA"]
Kantor je prije nekih 150 godina postavio jedan problem ovako:
zamislimo hotel sa beskonacno mnogo soba. sada zamislimo beskonacno takvih hotela. to je prebrojiv skup.
dakle...mene interesira, kako to moze biti prebrojiv skup ako smo ga vec definirali kao beskonacnog?! ako zamislimo da su ti hoteli jedan skup, jedino sto mi pada na pamet jest konstruiranje bijekcije sa tog skupa na skup N. ako postoji, onda je taj skup prebrojiv. medjutim, meni to nikako ne ide.
[/quote]
Oznacimo sa (i, j) j-tu sobu u i-tom hotelu. Sada imas nesto sto se moze opisati kao beskonacna matrica:
(1,1) (1,2) (1,3).....
(2,1) (2,2) (2,3).....
(3,1) (3,2) (3,3).....
....
....
....
OK, sada kupi sve te uredjene parove po 'dijagonalama', ovako:
(1,1), (1,2), (2,1), (1,3), (2,2), (3,1), ....
Odnosno, prvo pokupi sve kojima je zbroj koordinata 2, nakon toga 3, pa 4 itd. Ocito je da se uz mrvicu truda moze napisati i formula koja ostvaruje bijektivno preslikavanje izmedju |N x |N i |N.[/quote]
znaci, preslikava se sa vektorskog prostora NxN na N, rajt?! ispravi me ako grijesim.
[quote]
[quote]kakav je to skup koji nije element samog sebe?! ako gledamo logicki, takav skup ne postoji jer svaki skup sadrzi barem jedan element, samog sebe. kako je moguce matematicki definirati pojam koji je u suprotnosti sa zdravom logikom?![/quote]
:blueshock: :blueshock: :blueshock: :blueshock: :blueshock:
Kod Russelovog paradoksa upravo i jeste problem u tome sto nijedan skup ne moze sadrzavati samog sebe! (konkretno u ZF teoriji to je u suprotnosti s aksiomom utemeljenosti) [/quote]
nisi mi nista rekao sa ovime, dapace, dodatno si me zbunio :|
[quote]
Usput, jesi li se ikada zapitao sto je to zdrava logika?[/quote]
paaa, to bi trebalo biti nesto sto se samo po sebi podrazumijeva, bilo kao nekakva radnja koju treba napraviti bilo da se nesto ocigledno implicira...evo bukvalnog primjera: ja sam zedan, logicki je da cu ici popit vode (bilo prije, bilo kasnije).
[quote]
[quote]nadalje, tu se postavlja i pitanje: sto je to prazan skup?! ako definiramo prazan skup kao skup koji ima nista elemenata, onda znaci da taj skup ipak nije prazan, odnosno, on sadrzi jedan element, nista. a ako je nista element, onda je [b]nista[/b] [i]nesto[/i]...a to je nemoguce jer nesto sto ne postoji ne moze biti definirano kao nekakav element. molio bih vas da mi to objasnite. zahvaljujem se na aznji.[/quote]
Prazan skup je upravo skup bez elemenata. Ako ti pomaze zamisljaj ga kao {x | x != x} jer mi se cini da je formalna definicija preslozena za ovaj topic.
Vezano za prazan skup vec postoji jedan topic [url]http://degiorgi.math.hr/forum/viewtopic.php?t=2888[/url][/quote]
znaci, prazan skup je skup bez elemenata. ajmo onda pitati ovako...da li prazan skup uopce postoji ili je on izmisljen jer, kao sto sve ostale matematicke discipline, i teorija skupova mora imati nekakav, ajmo tako reci, neutralan element?! pod neutralnim mislim da je podskup svih skupova bez obzira kako definirali skup (ako se ne varam, prazan skup je podskup bilo kojeg skupa elemenata)?!
| mdoko (napisa): | | HijenA (napisa): |
Kantor je prije nekih 150 godina postavio jedan problem ovako:
zamislimo hotel sa beskonacno mnogo soba. sada zamislimo beskonacno takvih hotela. to je prebrojiv skup.
dakle...mene interesira, kako to moze biti prebrojiv skup ako smo ga vec definirali kao beskonacnog?! ako zamislimo da su ti hoteli jedan skup, jedino sto mi pada na pamet jest konstruiranje bijekcije sa tog skupa na skup N. ako postoji, onda je taj skup prebrojiv. medjutim, meni to nikako ne ide.
|
Oznacimo sa (i, j) j-tu sobu u i-tom hotelu. Sada imas nesto sto se moze opisati kao beskonacna matrica:
(1,1) (1,2) (1,3).....
(2,1) (2,2) (2,3).....
(3,1) (3,2) (3,3).....
....
....
....
OK, sada kupi sve te uredjene parove po 'dijagonalama', ovako:
(1,1), (1,2), (2,1), (1,3), (2,2), (3,1), ....
Odnosno, prvo pokupi sve kojima je zbroj koordinata 2, nakon toga 3, pa 4 itd. Ocito je da se uz mrvicu truda moze napisati i formula koja ostvaruje bijektivno preslikavanje izmedju |N x |N i |N. |
znaci, preslikava se sa vektorskog prostora NxN na N, rajt?! ispravi me ako grijesim.
| Citat: |
| Citat: | | kakav je to skup koji nije element samog sebe?! ako gledamo logicki, takav skup ne postoji jer svaki skup sadrzi barem jedan element, samog sebe. kako je moguce matematicki definirati pojam koji je u suprotnosti sa zdravom logikom?! |
    
Kod Russelovog paradoksa upravo i jeste problem u tome sto nijedan skup ne moze sadrzavati samog sebe! (konkretno u ZF teoriji to je u suprotnosti s aksiomom utemeljenosti) |
nisi mi nista rekao sa ovime, dapace, dodatno si me zbunio 
| Citat: |
Usput, jesi li se ikada zapitao sto je to zdrava logika? |
paaa, to bi trebalo biti nesto sto se samo po sebi podrazumijeva, bilo kao nekakva radnja koju treba napraviti bilo da se nesto ocigledno implicira...evo bukvalnog primjera: ja sam zedan, logicki je da cu ici popit vode (bilo prije, bilo kasnije).
| Citat: |
| Citat: | | nadalje, tu se postavlja i pitanje: sto je to prazan skup?! ako definiramo prazan skup kao skup koji ima nista elemenata, onda znaci da taj skup ipak nije prazan, odnosno, on sadrzi jedan element, nista. a ako je nista element, onda je nista nesto...a to je nemoguce jer nesto sto ne postoji ne moze biti definirano kao nekakav element. molio bih vas da mi to objasnite. zahvaljujem se na aznji. |
Prazan skup je upravo skup bez elemenata. Ako ti pomaze zamisljaj ga kao {x | x != x} jer mi se cini da je formalna definicija preslozena za ovaj topic.
Vezano za prazan skup vec postoji jedan topic http://degiorgi.math.hr/forum/viewtopic.php?t=2888 |
znaci, prazan skup je skup bez elemenata. ajmo onda pitati ovako...da li prazan skup uopce postoji ili je on izmisljen jer, kao sto sve ostale matematicke discipline, i teorija skupova mora imati nekakav, ajmo tako reci, neutralan element?! pod neutralnim mislim da je podskup svih skupova bez obzira kako definirali skup (ako se ne varam, prazan skup je podskup bilo kojeg skupa elemenata)?!
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 20:36 uto, 9. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova Postano: 20:36 uto, 9. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova |
    |
|
|
[quote="veky"][quote="HijenA"]eto...mene to vec duze vrijeme muci.[/quote]
Pa što nisi pitao prije? :-) [/quote]
a sta ces?! tek sam se sad sjetio da bi mogao pitat na forumu :-) jel vjerujes da me ova pitanja muce vec skoro godinu dana.
[quote]
[quote]Kantor je prije nekih 150 godina postavio jedan problem ovako:
zamislimo hotel sa beskonacno mnogo soba. sada zamislimo beskonacno takvih hotela. to je prebrojiv skup.[/quote]
_Što točno_ (je prebrojiv skup)? Pretpostavljam da _hotelâ_ ima (beskonačno) prebrojivo mnogo, i da _svaki_ od tih hotelâ ima (beskonačno) prebrojivo mnogo sobâ.[/quote]
meni je kolega ispricao taj problem. i rekao mi je da neki drugi matematicar koji je bio predsjednik(?!) udruge matematicara u parizu nije dao da se kantorovi clanci objavljuju jer je mislio da je nemoguce prebrojati beskonacne skupove. sta ako ih ima beskonacno (neprebrojivo) mnogo?!
[quote]
[quote]dakle...mene interesira, kako to moze biti prebrojiv skup ako smo ga vec definirali kao beskonacnog?![/quote]
_Koje_? Trenutno imaš hrpu skupova u igri, od kojih si neke definirao kao beskonačne. Konkretno, imaš skup hotelâ, H , i za svaki hotel h@H , imaš skup njegovih sobâ s_h . Naravno, osim svega toga, imaš i skup _svih_ soba u svim tim hotelima, S , što je zapravo S:=U_h@H s_h (unija svih s_h , po h iz H ). Ti si definirao da je skup H beskonačan, i da je za svaki h@H , skup s_h beskonačan.[/quote]
da, svaki hotel ima beskonacno mnogo soba, a hotela ima beskonacno mnogo.
[quote]
Ako je točna ona moja pretpostavka gore napisana, tada si rekao i više: da su skup H , i svi skupovi s_h , beskonačno _prebrojivi_, tj. bijektivni sa skupom \N .[/quote]
dobro...to sam shvatio. ako su prebrojivi. a to je veliko ako. a sto ako nisu prebrojivi?! onda znaci da ne postoji ta bijekcija?! jer, recimo, skup R je beskonacno neprebrojiv jer izmedju svakog realnog broja postoji beskonacno mnogo realnih brojeva bez obzira koliko oni bili mali.
[quote]
[quote] ako zamislimo da su ti hoteli jedan skup, jedino sto mi pada na pamet jest konstruiranje bijekcije sa tog skupa na skup N. ako postoji, onda je taj skup prebrojiv. medjutim, meni to nikako ne ide.[/quote]
To je pak trivijalno. Pretpostavka zadatka je da je H prebrojivo beskonačan. Ono što je malo manje trivijalno, jest da je i S prebrojivo beskonačan. A to je ono što je mdoko gore "dokazao" (do na onu "mrvicu truda", što ću ja popraviti: s f(i,j):=((i+j-1)povrh2)+i je zadana bijekcija između |Nx|N i |N ).[/quote]
zahvaljujem.
[quote]
[quote]osim toga, imam jos jedno pitanje (iako bi ono vise spadalo pod elementarnu). kakav je to skup koji nije element samog sebe?![/quote]
Recimo, prazan skup je takav. Ništa nije element praznog skupa, pa tako ni on sam.
Recimo, skup {1,2,3} je takav. Broj 1 je njegov element. Broj 2 je njegov element. Broj 3 je njegov element. No bilo što drugo, različito od brojeva 1 , 2 i 3 , _nije_ njegov element. Specijalno, skup {1,2,3} je različit i od broja 1 i od broja 2 i od broja 3 (i ovo se može dokazati, no uzmimo intuitivno da je to jasno), te on nije element skupa {1,2,3} , odnosno samog sebe.[/quote]
znaci, kad bi skup {1,2,3} izgledao {1,2,3,1,2,3}, iako je to nemoguce, onda bi on bio element samog sebe, rajt?! a sto se tice praznog skupa...ako definiramo prazan skup kao { x | x!=x }, onda nista nije element tog skupa. medjutim, ako ga definiramo kao 0={} onda nista jest element tog skupa jer se izmedju zagrada nalazi nista, a onda je nista element. to meni nikako nije jasno.
[quote]
Primijeti, on _jest_ svoj _podskup_, kao što je svaki skup podskup samog sebe. Ali nije svoj _element_ - štoviše, u ZF , standardnoj teoriji skupova, nijedan skup nije element samog sebe.[/quote]
da...pa to je samo po sebi jasno.
[quote]
[quote] ako gledamo logicki, takav skup ne postoji jer svaki skup sadrzi barem jedan element, samog sebe.[/quote]
Njet. Vjerojatno želiš zamijeniti riješ "element" rječju "podskup".
Vidi http://degiorgi.math.hr/forum/viewtopic.php?p=20454#20454 za dalje (ako ti se ne da sve čitati, traži (unutar citata) "on sadrži i ništa").[/quote]
ne kuzim...ako nesto nije matematicki pojam, zasto se moze onda nesto tako i opisati?! zar nije ista recenica: skup ima nista elemenata i skup nema niti jednog elementa?!
[quote]
[quote] kako je moguce matematicki definirati pojam koji je u suprotnosti sa zdravom logikom?! [/quote]
Easy. Pogledaj npr. Peanovu krivulju. ;-)
http://www.cut-the-knot.org/do_you_know/hilbert.shtml[/quote]
malo sam mutav danas...please explain ;)
[quote]
[quote]nadalje, tu se postavlja i pitanje: sto je to prazan skup?![/quote]
To je skup koji nema elemenata. Preciznije, to je skup 0 takav da za svaki x vrijedi !(x@0) (nije x element od 0 ).[/quote]
dobro...to sam shvatio.
[quote]
[quote] ako definiramo prazan skup kao skup koji ima nista elemenata, onda znaci da taj skup ipak nije prazan, odnosno, on sadrzi jedan element, nista.[/quote]
Wrong. U onom linku koji sam ti dao, odskrolaj koji ekran gore, do onog "No cat has eight tails.". Ovo je jezička pogreška.[/quote]
mozda sam dosadan, zar nije ta tvrdnja matematicki ispravna?! bez obzira sto nismo definirali nista, odnosno ako definiramo nista kao svojstvo praznog skupa?
[quote]
[quote] a ako je nista element, onda je [b]nista[/b] [i]nesto[/i]...a to je nemoguce jer nesto sto ne postoji ne moze biti definirano kao nekakav element.[/quote]
Slažem se. I zato
1) "Ništa" nije matematički pojam
2) prazan skup se ne definira pomoću "ništa", već na gornji način.
HTH,[/quote]
dobro...a sto ako nista definiramo kao svojstvo praznog skupa?! u tom slucaju, prazan skup je stvarno prazan, tj. njegovo svojstvo je da sadrzi nista. kao sto, recimo, za skup N definiramo prvi element i uvjet kako se sljedeci elementi pojavljuju.
| veky (napisa): | | HijenA (napisa): | | eto...mene to vec duze vrijeme muci. |
Pa što nisi pitao prije?  |
a sta ces?! tek sam se sad sjetio da bi mogao pitat na forumu  jel vjerujes da me ova pitanja muce vec skoro godinu dana. jel vjerujes da me ova pitanja muce vec skoro godinu dana.
| Citat: |
| Citat: | Kantor je prije nekih 150 godina postavio jedan problem ovako:
zamislimo hotel sa beskonacno mnogo soba. sada zamislimo beskonacno takvih hotela. to je prebrojiv skup. |
_Što točno_ (je prebrojiv skup)? Pretpostavljam da _hotelâ_ ima (beskonačno) prebrojivo mnogo, i da _svaki_ od tih hotelâ ima (beskonačno) prebrojivo mnogo sobâ. |
meni je kolega ispricao taj problem. i rekao mi je da neki drugi matematicar koji je bio predsjednik(?!) udruge matematicara u parizu nije dao da se kantorovi clanci objavljuju jer je mislio da je nemoguce prebrojati beskonacne skupove. sta ako ih ima beskonacno (neprebrojivo) mnogo?!
| Citat: |
| Citat: | | dakle...mene interesira, kako to moze biti prebrojiv skup ako smo ga vec definirali kao beskonacnog?! |
_Koje_? Trenutno imaš hrpu skupova u igri, od kojih si neke definirao kao beskonačne. Konkretno, imaš skup hotelâ, H , i za svaki hotel h@H , imaš skup njegovih sobâ s_h . Naravno, osim svega toga, imaš i skup _svih_ soba u svim tim hotelima, S , što je zapravo S:=U_h@H s_h (unija svih s_h , po h iz H ). Ti si definirao da je skup H beskonačan, i da je za svaki h@H , skup s_h beskonačan. |
da, svaki hotel ima beskonacno mnogo soba, a hotela ima beskonacno mnogo.
| Citat: |
Ako je točna ona moja pretpostavka gore napisana, tada si rekao i više: da su skup H , i svi skupovi s_h , beskonačno _prebrojivi_, tj. bijektivni sa skupom \N . |
dobro...to sam shvatio. ako su prebrojivi. a to je veliko ako. a sto ako nisu prebrojivi?! onda znaci da ne postoji ta bijekcija?! jer, recimo, skup R je beskonacno neprebrojiv jer izmedju svakog realnog broja postoji beskonacno mnogo realnih brojeva bez obzira koliko oni bili mali.
| Citat: |
| Citat: | | ako zamislimo da su ti hoteli jedan skup, jedino sto mi pada na pamet jest konstruiranje bijekcije sa tog skupa na skup N. ako postoji, onda je taj skup prebrojiv. medjutim, meni to nikako ne ide. |
To je pak trivijalno. Pretpostavka zadatka je da je H prebrojivo beskonačan. Ono što je malo manje trivijalno, jest da je i S prebrojivo beskonačan. A to je ono što je mdoko gore "dokazao" (do na onu "mrvicu truda", što ću ja popraviti: s f(i,j):=((i+j-1)povrh2)+i je zadana bijekcija između |Nx|N i |N ). |
zahvaljujem.
| Citat: |
| Citat: | | osim toga, imam jos jedno pitanje (iako bi ono vise spadalo pod elementarnu). kakav je to skup koji nije element samog sebe?! |
Recimo, prazan skup je takav. Ništa nije element praznog skupa, pa tako ni on sam.
Recimo, skup {1,2,3} je takav. Broj 1 je njegov element. Broj 2 je njegov element. Broj 3 je njegov element. No bilo što drugo, različito od brojeva 1 , 2 i 3 , _nije_ njegov element. Specijalno, skup {1,2,3} je različit i od broja 1 i od broja 2 i od broja 3 (i ovo se može dokazati, no uzmimo intuitivno da je to jasno), te on nije element skupa {1,2,3} , odnosno samog sebe. |
znaci, kad bi skup {1,2,3} izgledao {1,2,3,1,2,3}, iako je to nemoguce, onda bi on bio element samog sebe, rajt?! a sto se tice praznog skupa...ako definiramo prazan skup kao { x | x!=x }, onda nista nije element tog skupa. medjutim, ako ga definiramo kao 0={} onda nista jest element tog skupa jer se izmedju zagrada nalazi nista, a onda je nista element. to meni nikako nije jasno.
| Citat: |
Primijeti, on _jest_ svoj _podskup_, kao što je svaki skup podskup samog sebe. Ali nije svoj _element_ - štoviše, u ZF , standardnoj teoriji skupova, nijedan skup nije element samog sebe. |
da...pa to je samo po sebi jasno.
| Citat: |
| Citat: | | ako gledamo logicki, takav skup ne postoji jer svaki skup sadrzi barem jedan element, samog sebe. |
Njet. Vjerojatno želiš zamijeniti riješ "element" rječju "podskup".
Vidi http://degiorgi.math.hr/forum/viewtopic.php?p=20454#20454 za dalje (ako ti se ne da sve čitati, traži (unutar citata) "on sadrži i ništa"). |
ne kuzim...ako nesto nije matematicki pojam, zasto se moze onda nesto tako i opisati?! zar nije ista recenica: skup ima nista elemenata i skup nema niti jednog elementa?!
malo sam mutav danas...please explain 
| Citat: |
| Citat: | | nadalje, tu se postavlja i pitanje: sto je to prazan skup?! |
To je skup koji nema elemenata. Preciznije, to je skup 0 takav da za svaki x vrijedi !(x@0) (nije x element od 0 ). |
dobro...to sam shvatio.
| Citat: |
| Citat: | | ako definiramo prazan skup kao skup koji ima nista elemenata, onda znaci da taj skup ipak nije prazan, odnosno, on sadrzi jedan element, nista. |
Wrong. U onom linku koji sam ti dao, odskrolaj koji ekran gore, do onog "No cat has eight tails.". Ovo je jezička pogreška. |
mozda sam dosadan, zar nije ta tvrdnja matematicki ispravna?! bez obzira sto nismo definirali nista, odnosno ako definiramo nista kao svojstvo praznog skupa?
| Citat: |
| Citat: | | a ako je nista element, onda je nista nesto...a to je nemoguce jer nesto sto ne postoji ne moze biti definirano kao nekakav element. |
Slažem se. I zato
1) "Ništa" nije matematički pojam
2) prazan skup se ne definira pomoću "ništa", već na gornji način.
HTH, |
dobro...a sto ako nista definiramo kao svojstvo praznog skupa?! u tom slucaju, prazan skup je stvarno prazan, tj. njegovo svojstvo je da sadrzi nista. kao sto, recimo, za skup N definiramo prvi element i uvjet kako se sljedeci elementi pojavljuju.
|
|
| [Vrh] |
|
cinik
Forumaš(ica)


Pridružen/a: 27. 04. 2003. (23:34:09)
Postovi: (1FB)16
Spol: 
Lokacija: /proc/sys/cpu/
|
 Postano: 21:14 uto, 9. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova Postano: 21:14 uto, 9. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova |
    |
|
|
[quote="HijenA"]
meni je kolega ispricao taj problem. i rekao mi je da neki drugi matematicar koji je bio predsjednik(?!) udruge matematicara u parizu nije dao da se kantorovi clanci objavljuju jer je mislio da je nemoguce prebrojati beskonacne skupove. sta ako ih ima beskonacno (neprebrojivo) mnogo?!
[/quote]
Nije bio predsjednik nego urdenik nekoliko casopisa -- Kronecker (Kroneckerov simbol, ona deltica). On je bio konstruktivist -- vjerovao je da je "matematicko" ("ispravno", "tocno", "istinito"....) samo ono sto se moze eksplicitno konstruirati, tj. njemu nije bilo dosta da nesto iz aksioma postoji, vec da postoji "algoritam" kako to konstruirati.
[quote]
da, svaki hotel ima beskonacno mnogo soba, a hotela ima beskonacno mnogo.
[/quote]
Koliko beskonacno? Beskonacnost u smislu realnih brojeva (continuum) je veca od beskonacno prirodnih brojeva (prebrojiva beskonacnost). Realnih funkcija ima jos puuuuuno vise (jos jedna veca beskonacnost) i tako dalje i tako dalje. Kako god beskonacan skup bio, njegov partitivni ima vecu beskonacnost.
[quote]
znaci, kad bi skup {1,2,3} izgledao {1,2,3,1,2,3}, iako je to nemoguce, onda bi on bio element samog sebe, rajt?! a sto se tice praznog skupa...ako definiramo prazan skup kao { x | x!=x }, onda nista nije element tog skupa. medjutim, ako ga definiramo kao 0={} onda nista jest element tog skupa jer se izmedju zagrada nalazi nista, a onda je nista element. to meni nikako nije jasno.
[/quote]
{1,2,3}={1,2,3,1,2,3} i podskup mu je, ali nije element samoga sebe. Skup kojemu je on sam element bi izgledao nekako ovako:
[latex] S=\{S,\ldots\}[/latex]
Do neke mjere eskpandirano:
[latex] S=\{\{\{\{\{\{\{\{\{\{\{S,\ldots\},\ldots\},\ldots\},\ldots\},\ldots\},\ldots\},\ldots\},\ldots\},\ldots\},\ldots\},\ldots\},\ldots\}[/latex]
[quote][quote]
[quote] kako je moguce matematicki definirati pojam koji je u suprotnosti sa zdravom logikom?! [/quote]
Easy. Pogledaj npr. Peanovu krivulju. ;-)
http://www.cut-the-knot.org/do_you_know/hilbert.shtml[/quote]
malo sam mutav danas...please explain ;)
[/quote]
To ti je krivulja -- dakle crta -- dakle beskonacno tanki otisak tehnicke na ultrasuperduperfinom papiru, koji, bez obzira na nedostatak vlastite sirine, pokriva CIJELU povrsinu kvadrata i jos samu sebe sijece.
[quote]
dobro...a sto ako nista definiramo kao svojstvo praznog skupa?! u tom slucaju, prazan skup je stvarno prazan, tj. njegovo svojstvo je da sadrzi nista. kao sto, recimo, za skup N definiramo prvi element i uvjet kako se sljedeci elementi pojavljuju.[/quote]
Kad se vec prazno filozofira, ajmo filozofirati.
Dakle, svojstvo skupa [latex]S=\{2,4,6,....\}[/latex] jest parnost njegovih elemenata.
Sta to znaci? To znaci da su (tj. [b]jesu, postoje[/b]) SVI njegovi elementi PRIODNI BROJEVI, koji jos zadovoljavaju uvjet da za svaki [latex]n\in S[/latex] [b]postoji[/b] takav prirodan broj k da je za [latex]n=2k[/latex]
Dakle, ako nam je nista svojstvo skupa [latex]\emptyset[/latex], to znaci da "svi njegovi elementi" zadovoljavaju svojstvo nistavila -- nepostojanja. Ne [b]praznosti[/b], vec [b] nepostojanja[/b]. Dakle [latex]x\in\emptyset[/latex] znaci da [latex]x[/latex] [b] ne postoji[/b], sto je onda lijepo definirano izrazom [latex]x\neq x[/latex], jer sve sto postoji je iskljucivo jednako samome sebi, pa je to dobar nacin za opisati nepostojanje. Ako zelis rijesiti nesto na matematicki nacin, prezentiras to simbolima sa kojima mozes baratati i onda se petljas samo sa tim simbolima i nadas se da oni dobro prate tvoju intuitivnu logiku. No, kojiput se desi da covjek ne zna tocno sta je sta u njegovoj vlastitoj logici, pa ne razlikuje na kojoj se razini koji objekt o kojemu razmislja nalazi.
'ave fun!
Sinisa
| HijenA (napisa): |
meni je kolega ispricao taj problem. i rekao mi je da neki drugi matematicar koji je bio predsjednik(?!) udruge matematicara u parizu nije dao da se kantorovi clanci objavljuju jer je mislio da je nemoguce prebrojati beskonacne skupove. sta ako ih ima beskonacno (neprebrojivo) mnogo?!
|
Nije bio predsjednik nego urdenik nekoliko casopisa – Kronecker (Kroneckerov simbol, ona deltica). On je bio konstruktivist – vjerovao je da je "matematicko" ("ispravno", "tocno", "istinito"....) samo ono sto se moze eksplicitno konstruirati, tj. njemu nije bilo dosta da nesto iz aksioma postoji, vec da postoji "algoritam" kako to konstruirati.
| Citat: |
da, svaki hotel ima beskonacno mnogo soba, a hotela ima beskonacno mnogo.
|
Koliko beskonacno? Beskonacnost u smislu realnih brojeva (continuum) je veca od beskonacno prirodnih brojeva (prebrojiva beskonacnost). Realnih funkcija ima jos puuuuuno vise (jos jedna veca beskonacnost) i tako dalje i tako dalje. Kako god beskonacan skup bio, njegov partitivni ima vecu beskonacnost.
| Citat: |
znaci, kad bi skup {1,2,3} izgledao {1,2,3,1,2,3}, iako je to nemoguce, onda bi on bio element samog sebe, rajt?! a sto se tice praznog skupa...ako definiramo prazan skup kao { x | x!=x }, onda nista nije element tog skupa. medjutim, ako ga definiramo kao 0={} onda nista jest element tog skupa jer se izmedju zagrada nalazi nista, a onda je nista element. to meni nikako nije jasno.
|
{1,2,3}={1,2,3,1,2,3} i podskup mu je, ali nije element samoga sebe. Skup kojemu je on sam element bi izgledao nekako ovako:
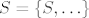
Do neke mjere eskpandirano:
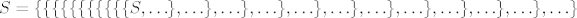
| Citat: |
malo sam mutav danas...please explain 
|
To ti je krivulja – dakle crta – dakle beskonacno tanki otisak tehnicke na ultrasuperduperfinom papiru, koji, bez obzira na nedostatak vlastite sirine, pokriva CIJELU povrsinu kvadrata i jos samu sebe sijece.
| Citat: |
dobro...a sto ako nista definiramo kao svojstvo praznog skupa?! u tom slucaju, prazan skup je stvarno prazan, tj. njegovo svojstvo je da sadrzi nista. kao sto, recimo, za skup N definiramo prvi element i uvjet kako se sljedeci elementi pojavljuju. |
Kad se vec prazno filozofira, ajmo filozofirati.
Dakle, svojstvo skupa 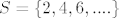 jest parnost njegovih elemenata. jest parnost njegovih elemenata.
Sta to znaci? To znaci da su (tj. jesu, postoje) SVI njegovi elementi PRIODNI BROJEVI, koji jos zadovoljavaju uvjet da za svaki 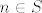 postoji takav prirodan broj k da je za postoji takav prirodan broj k da je za 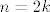
Dakle, ako nam je nista svojstvo skupa  , to znaci da "svi njegovi elementi" zadovoljavaju svojstvo nistavila – nepostojanja. Ne praznosti, vec nepostojanja. Dakle , to znaci da "svi njegovi elementi" zadovoljavaju svojstvo nistavila – nepostojanja. Ne praznosti, vec nepostojanja. Dakle 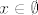 znaci da znaci da  ne postoji, sto je onda lijepo definirano izrazom ne postoji, sto je onda lijepo definirano izrazom 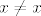 , jer sve sto postoji je iskljucivo jednako samome sebi, pa je to dobar nacin za opisati nepostojanje. Ako zelis rijesiti nesto na matematicki nacin, prezentiras to simbolima sa kojima mozes baratati i onda se petljas samo sa tim simbolima i nadas se da oni dobro prate tvoju intuitivnu logiku. No, kojiput se desi da covjek ne zna tocno sta je sta u njegovoj vlastitoj logici, pa ne razlikuje na kojoj se razini koji objekt o kojemu razmislja nalazi. , jer sve sto postoji je iskljucivo jednako samome sebi, pa je to dobar nacin za opisati nepostojanje. Ako zelis rijesiti nesto na matematicki nacin, prezentiras to simbolima sa kojima mozes baratati i onda se petljas samo sa tim simbolima i nadas se da oni dobro prate tvoju intuitivnu logiku. No, kojiput se desi da covjek ne zna tocno sta je sta u njegovoj vlastitoj logici, pa ne razlikuje na kojoj se razini koji objekt o kojemu razmislja nalazi.
'ave fun!
Sinisa
_________________
Oslobodjen Senata.
|
|
| [Vrh] |
|
fmb
Forumaš(ica)


Pridružen/a: 07. 02. 2004. (12:34:47)
Postovi: (B6)16
|
|
| [Vrh] |
|
fmb
Forumaš(ica)


Pridružen/a: 07. 02. 2004. (12:34:47)
Postovi: (B6)16
|
 Postano: 11:08 sri, 10. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova Postano: 11:08 sri, 10. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova |
    |
|
|
[quote="HijenA"]
znaci, preslikava se sa vektorskog prostora NxN na N, rajt?! ispravi me ako grijesim.[/quote]
NxN nije vektorski prostor. A u ovom kontekstu ga uzimamo iskljucivo kao skup. To je dvostruko vazno:
1- zato jer u teoriji skupova algebarske strukture nisu bitne, a ponajmanje unaprijed zadane (cak i uredjaji, ako se definiraju, nisu a priori oni prirodni). U teoriji skupova (i citavoj matematici) ako pricamo o "velicini" nekog skupa tj. broju njegovih elemenata ne uzimamo u obzir nikakvu dodatnu strukturu na tom skupu (algebarsku, uredjajnu, ... tj. ne pretpostavljamo da se elementi tog skupa mogu npr. zbrajati ili da je 1<2 ako su 1 i 2 elementi tog skupa).
2- Ovo je greska i bez obzira na teoriju skupova jer da je NxN vektorski prostor morao bi biti "invarijantan" na mnozenje realnim ili kompleksnim brojevima tj. morali bi biti npr. za (2,2) iz NxN da pomnozen s npr. e bude i dalje u NxN, a nije jer e(2,2)=(2e,2e), a 2e nije prirodan broj.
Jedna mala napomena za kraj:Kad je Cantor pokazao da duzina i kvadrat imaju jednako mnogo elemenata, ostao je zbunjen ("Vidim, ali ne vjerujem!") jer se postavilo pitanje kako onda razlikovati dimenzije ako sve dimenzije imaju jednako elemenata (duzina, kvadrat, kocka, hiperkocka ....) Odgovor je dao Brouwer, iako ga je vec Cantor naslutio: razlika je u nepostojanju neprekidnih bijekcija. Hocu reci: postoji bijekcija s duzine na kvadrat, ali ne neprekidna. A neprekidnost nije pojam iz teorije skupova, nego "nad" teorijom skupova izgradjenom disciplinom topologije...
FMB :patkica:
| HijenA (napisa): |
znaci, preslikava se sa vektorskog prostora NxN na N, rajt?! ispravi me ako grijesim. |
NxN nije vektorski prostor. A u ovom kontekstu ga uzimamo iskljucivo kao skup. To je dvostruko vazno:
1- zato jer u teoriji skupova algebarske strukture nisu bitne, a ponajmanje unaprijed zadane (cak i uredjaji, ako se definiraju, nisu a priori oni prirodni). U teoriji skupova (i citavoj matematici) ako pricamo o "velicini" nekog skupa tj. broju njegovih elemenata ne uzimamo u obzir nikakvu dodatnu strukturu na tom skupu (algebarsku, uredjajnu, ... tj. ne pretpostavljamo da se elementi tog skupa mogu npr. zbrajati ili da je 1<2 ako su 1 i 2 elementi tog skupa).
2- Ovo je greska i bez obzira na teoriju skupova jer da je NxN vektorski prostor morao bi biti "invarijantan" na mnozenje realnim ili kompleksnim brojevima tj. morali bi biti npr. za (2,2) iz NxN da pomnozen s npr. e bude i dalje u NxN, a nije jer e(2,2)=(2e,2e), a 2e nije prirodan broj.
Jedna mala napomena za kraj:Kad je Cantor pokazao da duzina i kvadrat imaju jednako mnogo elemenata, ostao je zbunjen ("Vidim, ali ne vjerujem!") jer se postavilo pitanje kako onda razlikovati dimenzije ako sve dimenzije imaju jednako elemenata (duzina, kvadrat, kocka, hiperkocka ....) Odgovor je dao Brouwer, iako ga je vec Cantor naslutio: razlika je u nepostojanju neprekidnih bijekcija. Hocu reci: postoji bijekcija s duzine na kvadrat, ali ne neprekidna. A neprekidnost nije pojam iz teorije skupova, nego "nad" teorijom skupova izgradjenom disciplinom topologije...
FMB 
_________________
"Have patience. Go where you must, and hope."
(Gandalf in J.R.R.Tolkien's "The Lord of the Rings")
|
|
| [Vrh] |
|
fmb
Forumaš(ica)


Pridružen/a: 07. 02. 2004. (12:34:47)
Postovi: (B6)16
|
 Postano: 11:13 sri, 10. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova Postano: 11:13 sri, 10. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova |
    |
|
|
[quote="HijenA"]
[quote]
[quote]kakav je to skup koji nije element samog sebe?! ako gledamo logicki, takav skup ne postoji jer svaki skup sadrzi barem jedan element, samog sebe. kako je moguce matematicki definirati pojam koji je u suprotnosti sa zdravom logikom?![/quote]
:blueshock: :blueshock: :blueshock: :blueshock: :blueshock:
Kod Russelovog paradoksa upravo i jeste problem u tome sto nijedan skup ne moze sadrzavati samog sebe! (konkretno u ZF teoriji to je u suprotnosti s aksiomom utemeljenosti) [/quote]
nisi mi nista rekao sa ovime, dapace, dodatno si me zbunio :|
[/quote]
Pojednostavimo: u naivnoj teoriji skupova, a to je ona kakva se uci u skoli i na kojoj je utemeljena sva "standardna" matematika, a koja se na (od matematicara obicno zahtijevanu) aksiomatsku osnovu stavlja preko tzv. ZF-aksioma, nije moguce da skup bude element samog sebe. Zasto? Zato jer ako to dozvolimo, za posljedicu cemo dobiti paradokse i kontradikcije u teoriji. S tim je i pocelo: Cantor nije imao aksiome, ali je otkrio paradokse kao onaj o brijacu koji brije samog sebe (ekvivalentno nepostojanju skupa svih skupova). Da se takve cudne situacije izbjegnu (a da pritom svi dokaza i dalje vrijede) kao jedan od aksioma se 20ih godina 20.st. uzelo da nijedan skup ne smije sadrzavat samog sebe (to je tzv. aksiom fundiranosti).
FMB :patkica:
| HijenA (napisa): |
| Citat: |
| Citat: | | kakav je to skup koji nije element samog sebe?! ako gledamo logicki, takav skup ne postoji jer svaki skup sadrzi barem jedan element, samog sebe. kako je moguce matematicki definirati pojam koji je u suprotnosti sa zdravom logikom?! |
    
Kod Russelovog paradoksa upravo i jeste problem u tome sto nijedan skup ne moze sadrzavati samog sebe! (konkretno u ZF teoriji to je u suprotnosti s aksiomom utemeljenosti) |
nisi mi nista rekao sa ovime, dapace, dodatno si me zbunio 
|
Pojednostavimo: u naivnoj teoriji skupova, a to je ona kakva se uci u skoli i na kojoj je utemeljena sva "standardna" matematika, a koja se na (od matematicara obicno zahtijevanu) aksiomatsku osnovu stavlja preko tzv. ZF-aksioma, nije moguce da skup bude element samog sebe. Zasto? Zato jer ako to dozvolimo, za posljedicu cemo dobiti paradokse i kontradikcije u teoriji. S tim je i pocelo: Cantor nije imao aksiome, ali je otkrio paradokse kao onaj o brijacu koji brije samog sebe (ekvivalentno nepostojanju skupa svih skupova). Da se takve cudne situacije izbjegnu (a da pritom svi dokaza i dalje vrijede) kao jedan od aksioma se 20ih godina 20.st. uzelo da nijedan skup ne smije sadrzavat samog sebe (to je tzv. aksiom fundiranosti).
FMB 
_________________
"Have patience. Go where you must, and hope."
(Gandalf in J.R.R.Tolkien's "The Lord of the Rings")
|
|
| [Vrh] |
|
fmb
Forumaš(ica)


Pridružen/a: 07. 02. 2004. (12:34:47)
Postovi: (B6)16
|
 Postano: 11:19 sri, 10. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova Postano: 11:19 sri, 10. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova |
    |
|
|
[quote="HijenA"]znaci, prazan skup je skup bez elemenata. ajmo onda pitati ovako...da li prazan skup uopce postoji ili je on izmisljen jer, kao sto sve ostale matematicke discipline, i teorija skupova mora imati nekakav, ajmo tako reci, neutralan element?! pod neutralnim mislim da je podskup svih skupova bez obzira kako definirali skup (ako se ne varam, prazan skup je podskup bilo kojeg skupa elemenata)?![/quote]
Kao aksiom se uzima da prazan skup postoji: "Postoji skup bez ijednog elementa". Lako se provjeri da je taj skup jedinstveno odredjen, ako znamo prvi aksiom (dva skupa su jednaka tocno ako imaju iste elemente).
On nije uveden radi "neutralnog" elementa (iako mu je to jedno zgodno svojstvo koje je dodatni razlog za zahtijevanje njegova postojanja), nego zato jer postojanje svih matematickih skupova mozemo izvesti ako znamo da postoji prazan skup i ako imamo ostale aksiome (koji daju nacine konstrukcije drugih skupova iz vec danih). Ekvivalentno bi bilo kao aksiom zahtijevati "Postoji skup." No ovako je jednostavnije jer ne moramo ulaziti u prirodu elemenata tog skupa. E, a jedna od cari teorije skupova je da se iz praznog skupa mogu konstruirati npr. svi brojevi (prirodni, racionalni, realni, kompleksni...)
FMB :patkica:
| HijenA (napisa): | | znaci, prazan skup je skup bez elemenata. ajmo onda pitati ovako...da li prazan skup uopce postoji ili je on izmisljen jer, kao sto sve ostale matematicke discipline, i teorija skupova mora imati nekakav, ajmo tako reci, neutralan element?! pod neutralnim mislim da je podskup svih skupova bez obzira kako definirali skup (ako se ne varam, prazan skup je podskup bilo kojeg skupa elemenata)?! |
Kao aksiom se uzima da prazan skup postoji: "Postoji skup bez ijednog elementa". Lako se provjeri da je taj skup jedinstveno odredjen, ako znamo prvi aksiom (dva skupa su jednaka tocno ako imaju iste elemente).
On nije uveden radi "neutralnog" elementa (iako mu je to jedno zgodno svojstvo koje je dodatni razlog za zahtijevanje njegova postojanja), nego zato jer postojanje svih matematickih skupova mozemo izvesti ako znamo da postoji prazan skup i ako imamo ostale aksiome (koji daju nacine konstrukcije drugih skupova iz vec danih). Ekvivalentno bi bilo kao aksiom zahtijevati "Postoji skup." No ovako je jednostavnije jer ne moramo ulaziti u prirodu elemenata tog skupa. E, a jedna od cari teorije skupova je da se iz praznog skupa mogu konstruirati npr. svi brojevi (prirodni, racionalni, realni, kompleksni...)
FMB 
_________________
"Have patience. Go where you must, and hope."
(Gandalf in J.R.R.Tolkien's "The Lord of the Rings")
|
|
| [Vrh] |
|
fmb
Forumaš(ica)


Pridružen/a: 07. 02. 2004. (12:34:47)
Postovi: (B6)16
|
 Postano: 11:22 sri, 10. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova Postano: 11:22 sri, 10. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova |
    |
|
|
[quote="HijenA"]
meni je kolega ispricao taj problem. i rekao mi je da neki drugi matematicar koji je bio predsjednik(?!) udruge matematicara u parizu nije dao da se kantorovi clanci objavljuju jer je mislio da je nemoguce prebrojati beskonacne skupove. sta ako ih ima beskonacno (neprebrojivo) mnogo?!
[/quote]
Cantor jest imao problema s objavljivanjem clanaka, a osoba koja je bila na celu opozicije bio je Leopold Kronecker, jedan od urednika tada najjaceg matematickog casopisa "Crelle's Jorunal"-a. Razlog protivljenja je biop u tome sto je Kronecker bio zagovornik matematicke filozofije konstruktivizma, koja za valjan dokaz egzistencije nekog objekta zahtijeva postupak njegove konstrukcije. Stoga konstruktiviste muci vec sam dokaz egzistencije jednog transcendentnog borja, a pogotovu Cantorovi dokazi iz kojih npr. trivijalno slijedi postojanje beskonacno mnogo transcendentnih brojeva (a nema nacina da iti jedan od njih konsturiramo).
FMB :patkica:
| HijenA (napisa): |
meni je kolega ispricao taj problem. i rekao mi je da neki drugi matematicar koji je bio predsjednik(?!) udruge matematicara u parizu nije dao da se kantorovi clanci objavljuju jer je mislio da je nemoguce prebrojati beskonacne skupove. sta ako ih ima beskonacno (neprebrojivo) mnogo?!
|
Cantor jest imao problema s objavljivanjem clanaka, a osoba koja je bila na celu opozicije bio je Leopold Kronecker, jedan od urednika tada najjaceg matematickog casopisa "Crelle's Jorunal"-a. Razlog protivljenja je biop u tome sto je Kronecker bio zagovornik matematicke filozofije konstruktivizma, koja za valjan dokaz egzistencije nekog objekta zahtijeva postupak njegove konstrukcije. Stoga konstruktiviste muci vec sam dokaz egzistencije jednog transcendentnog borja, a pogotovu Cantorovi dokazi iz kojih npr. trivijalno slijedi postojanje beskonacno mnogo transcendentnih brojeva (a nema nacina da iti jedan od njih konsturiramo).
FMB 
_________________
"Have patience. Go where you must, and hope."
(Gandalf in J.R.R.Tolkien's "The Lord of the Rings")
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 17:16 sri, 10. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova Postano: 17:16 sri, 10. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova |
    |
|
|
[quote="HijenA"]nadalje, tu se postavlja i pitanje: sto je to prazan skup?! ako definiramo prazan skup kao skup koji ima nista elemenata, onda znaci da taj skup ipak nije prazan, odnosno, on sadrzi jedan element, nista. a ako je nista element, onda je [b]nista[/b] [i]nesto[/i]...a to je nemoguce jer nesto sto ne postoji ne moze biti definirano kao nekakav element.[/quote]
Zasto studenti ne vole prazan skup? Na onom topicu u Elementarnoj ga je isto netko poljuvao... :cry:
Meni je prazan skup najdrazi od svih skupova :inlove: [url=http://degiorgi.math.hr/forum/viewtopic.php?t=1499]Vidi[/url] kakve se lijepe relacije moze dobiti prebrojavanjem elemenata praznog skupa :) (virtualne surjekcije)
| HijenA (napisa): | | nadalje, tu se postavlja i pitanje: sto je to prazan skup?! ako definiramo prazan skup kao skup koji ima nista elemenata, onda znaci da taj skup ipak nije prazan, odnosno, on sadrzi jedan element, nista. a ako je nista element, onda je nista nesto...a to je nemoguce jer nesto sto ne postoji ne moze biti definirano kao nekakav element. |
Zasto studenti ne vole prazan skup? Na onom topicu u Elementarnoj ga je isto netko poljuvao... 
Meni je prazan skup najdrazi od svih skupova  Vidi kakve se lijepe relacije moze dobiti prebrojavanjem elemenata praznog skupa Vidi kakve se lijepe relacije moze dobiti prebrojavanjem elemenata praznog skupa  (virtualne surjekcije) (virtualne surjekcije)
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
Zadnja promjena: krcko; 22:40 sri, 10. 11. 2004; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 17:21 sri, 10. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova Postano: 17:21 sri, 10. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova |
    |
|
|
[quote="krcko"][quote="HijenA"]nadalje, tu se postavlja i pitanje: sto je to prazan skup?! ako definiramo prazan skup kao skup koji ima nista elemenata, onda znaci da taj skup ipak nije prazan, odnosno, on sadrzi jedan element, nista. a ako je nista element, onda je [b]nista[/b] [i]nesto[/i]...a to je nemoguce jer nesto sto ne postoji ne moze biti definirano kao nekakav element.[/quote]
Zasto studenti ne vole prazan skup? Na onom topicu u Elementarnoj ga je isto netko poljuvao... :cry:
Meni je prazan skup najdrazi od svih skupova. [url=http://degiorgi.math.hr/forum/viewtopic.php?t=1499]Vidi[/url] kakve se lijepe relacije moze dobiti prebrojavanjem elemenata praznog skupa :) (virtualne surjekcije)[/quote]
nije da ga ja ne volim. ali, ovaj me paradox mucio dok god se nisu javili doticni asistenti/studenti koji su mi to i objasnili. no, smatram da je moje pitanje na mjestu.
| krcko (napisa): | | HijenA (napisa): | | nadalje, tu se postavlja i pitanje: sto je to prazan skup?! ako definiramo prazan skup kao skup koji ima nista elemenata, onda znaci da taj skup ipak nije prazan, odnosno, on sadrzi jedan element, nista. a ako je nista element, onda je nista nesto...a to je nemoguce jer nesto sto ne postoji ne moze biti definirano kao nekakav element. |
Zasto studenti ne vole prazan skup? Na onom topicu u Elementarnoj ga je isto netko poljuvao... 
Meni je prazan skup najdrazi od svih skupova. Vidi kakve se lijepe relacije moze dobiti prebrojavanjem elemenata praznog skupa  (virtualne surjekcije) (virtualne surjekcije) |
nije da ga ja ne volim. ali, ovaj me paradox mucio dok god se nisu javili doticni asistenti/studenti koji su mi to i objasnili. no, smatram da je moje pitanje na mjestu.
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 22:26 sri, 10. 11. 2004 Naslov: Postano: 22:26 sri, 10. 11. 2004 Naslov: |
    |
|
|
[quote="HijenA"]zahvaljujem se svim odgovorima. jos samo jedna stvar koju sam napomenuo. da li su izjave "prazan skup je skup koji ne sadrzi niti jedan element" i "prazan skup je skup koji sadrzi nista elemenata" ekvivalentne, iz matematickog gledista?! jos samo to...[/quote]
I dalje ostajem pri tome da "ništa" (u ovom kontekstu) nije matematički pojam, pa pitanje nije dobro definirano. No ako "sadrži ništa elemenata" upravo definiraš kao "ne sadrži x , za bilo koji x ", tada te izjave jesu ekvivalentne, naravno. :-)
| HijenA (napisa): | | zahvaljujem se svim odgovorima. jos samo jedna stvar koju sam napomenuo. da li su izjave "prazan skup je skup koji ne sadrzi niti jedan element" i "prazan skup je skup koji sadrzi nista elemenata" ekvivalentne, iz matematickog gledista?! jos samo to... |
I dalje ostajem pri tome da "ništa" (u ovom kontekstu) nije matematički pojam, pa pitanje nije dobro definirano. No ako "sadrži ništa elemenata" upravo definiraš kao "ne sadrži x , za bilo koji x ", tada te izjave jesu ekvivalentne, naravno. 
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 22:32 sri, 10. 11. 2004 Naslov: Postano: 22:32 sri, 10. 11. 2004 Naslov: |
    |
|
|
[quote="veky"][quote="HijenA"]zahvaljujem se svim odgovorima. jos samo jedna stvar koju sam napomenuo. da li su izjave "prazan skup je skup koji ne sadrzi niti jedan element" i "prazan skup je skup koji sadrzi nista elemenata" ekvivalentne, iz matematickog gledista?! jos samo to...[/quote]
I dalje ostajem pri tome da "ništa" (u ovom kontekstu) nije matematički pojam, pa pitanje nije dobro definirano. No ako "sadrži ništa elemenata" upravo definiraš kao "ne sadrži x , za bilo koji x ", tada te izjave jesu ekvivalentne, naravno. :-)[/quote]
zahvaljujem...to smo rascistili :) :) :) :D
| veky (napisa): | | HijenA (napisa): | | zahvaljujem se svim odgovorima. jos samo jedna stvar koju sam napomenuo. da li su izjave "prazan skup je skup koji ne sadrzi niti jedan element" i "prazan skup je skup koji sadrzi nista elemenata" ekvivalentne, iz matematickog gledista?! jos samo to... |
I dalje ostajem pri tome da "ništa" (u ovom kontekstu) nije matematički pojam, pa pitanje nije dobro definirano. No ako "sadrži ništa elemenata" upravo definiraš kao "ne sadrži x , za bilo koji x ", tada te izjave jesu ekvivalentne, naravno.  |
zahvaljujem...to smo rascistili    
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 23:01 sri, 10. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova Postano: 23:01 sri, 10. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova |
    |
|
|
[quote="HijenA"]...jer je mislio da je nemoguce prebrojati beskonacne skupove. sta ako ih ima beskonacno (neprebrojivo) mnogo?![/quote]
Izraz "neprebrojiv" se definira kao "ima više elemenata od skupa \N ", i nema baš puno veze s "brojanjem" kako se ono obično shvaća. O tome je već bilo govora po Forumu, npr. http://degiorgi.math.hr/forum/viewtopic.php?t=2465 .
Inače, Cantor je (s razlogom, u društvu u kojem je živio) bio jako oprezan s beskonačnošću... "infinitno" je bilo i iz njegove perspektive Božje, nedohvatljivo ljudima (i označavalo nešto što bismo danas zvali pravim klasama), dok se on bavio samo "_trans_finitnim", dakle onim što je "malo veće od konačnog" (ali još uvijek ljudskom umu dokučivo).
[quote]da, svaki hotel ima beskonacno mnogo soba, a hotela ima beskonacno mnogo.[/quote]
Ali samo to za problem nije dovoljno - treba ih biti prebrojivo mnogo. Bar ovaj gornji dokaz prolazi samo za prebrojive skupove.
[quote]dobro...to sam shvatio. ako su prebrojivi. a to je veliko ako. a sto ako nisu prebrojivi?! onda znaci da ne postoji ta bijekcija?![/quote]
Možda postoji. No za to nam trebaju jače pretpostavke.
Npr. ako prihvatimo nešto što se zove ZFC (standardna teorija skupova s _aksiomom izbora_), izlazi da je svaki beskonačni kardinalni broj ekvipotentan sa svojim kvadratom. Dakle, ne samo da |Nx|N ima jednako mnogo elemenata kao |N , već bilo koji beskonačni skup S ima jednako mnogo elemenata kao SxS .
Za mnoge "konkretne" skupove, however, puni ZFC nam ipak ne treba - npr. već u ZF se može vidjeti da je |Rx|R ekvipotentan s |R - kompleksnih brojeva ima jednako koliko i realnih.
[quote] jer, recimo, skup R je beskonacno neprebrojiv jer izmedju svakog realnog broja postoji beskonacno mnogo realnih brojeva bez obzira koliko oni bili mali.[/quote]
A bunch of parse errors... :-/
no što god da si htio reći, čini mi se da isto vrijedi i za |Q , a |Q je prebrojiv. Gustoća uređaja nema puno veze s potpunošću.
No kao što rekoh gore, vrijedi analogna tvrdnja i za |R - ako imaš kontinuum hotelâ, i u svakom od njih kontinuum sobâ, tada i ukupno imaš kontinuum sobâ.
[quote]znaci, kad bi skup {1,2,3} izgledao {1,2,3,1,2,3}, iako je to nemoguce,[/quote]
Ovisi. Što se mene tiče, {1,2,3,1,2,3} je samo drugi, čudniji, zapis za {1,2,3} (kao što je npr. 34/51 drugi, čudniji zapis za 2/3 ). Postoje ljudi koji smatraju {1,2,3,1,2,3} ilegalnom oznakom za skup, no takvi ljudi IME obično nisu svjesni da ih to sprečava npr. govoriti o skupu {a,b} ako nisu sigurni da je a != b ... [:-P]
[quote] onda bi on bio element samog sebe, rajt?![/quote]
Ne. I dalje su njegovi elementi samo 1 , 2 i 3 , a ne S .
[quote] a sto se tice praznog skupa...ako definiramo prazan skup kao { x | x!=x }, onda nista nije element tog skupa. medjutim, ako ga definiramo kao 0={} onda nista jest element tog skupa jer se izmedju zagrada nalazi nista, a onda je nista element. to meni nikako nije jasno.[/quote]
Niti meni. Kao što rekoh, "ništa" nije matematički pojam. To je samo fraza u hrvatskom jeziku kojom se nešto opisuje (i vodi do čudnih dvoznačnosti, poput ovog gore). Budući da math-jezik to može puno preciznije opisati, kvantifikatorima, njemu pojam "ništa" (u ovom kontekstu) ne treba.
Ti možeš reći "ništa nije element od 0 ", ako definiraš da ti to znači [latex]\forall x(x\not\in\emptyset)[/latex]. Također možeš reći i "ništa jest element od 0 ", ako definiraš da ti _to_ znači [latex]\forall x(x\not\in\emptyset)[/latex]. But you can't have it both ways. Stvar je samo u hrvatskom jeziku, i u njegovom čudnom shvaćanju dvostruke negacije.
[quote][quote]štoviše, u ZF , standardnoj teoriji skupova, nijedan skup nije element samog sebe.[/quote]
da...pa to je samo po sebi jasno.[/quote]
Ne mora biti... postoje teorije vrlo slične standardnoj teoriji skupova, npr. ZFA , u kojima to eksplicitno ne vrijedi - _postoji_ skup koji je element samog sebe.
[quote="FMB"]nije moguce da skup bude element samog sebe. Zasto? Zato jer ako to dozvolimo, za posljedicu cemo dobiti paradokse i kontradikcije u teoriji. [/quote]
Nećemo. ;-)
Možda zanimljivije, pretpostavka o utemeljenosti (ie, da nema "ciklusa" u relaciji "biti element") zapravo _nije_ essentially potrebna (iako je psihološki nesumnjivo lakše s njom raditi teoriju skupova) - može se dokazati da u teoriji ZF-Foundation postoji unutrašnji model (relativni dokaz konzistentnosti) kompletne teorije ZF . Skica dokaza: izgrade se (wellfounded) ordinali, i preko njih i partitivnog skupa, cijela kumulativna hijerarhija. Pokaže se da ona pokupi upravo ono što treba - cijeli ZF vrijedi unutar nje, a svi "loši" skupovi (koji nisu dobro utemeljeni relacijom @ ) ostanu vani.
Slučajno znam jer ima veze s mojim magistarskim. ;-)
[quote][quote]http://www.cut-the-knot.org/do_you_know/hilbert.shtml[/quote]
malo sam mutav danas...please explain ;)[/quote]
Peanova krivulja se valjda navodi kao standardni primjer "logičke konstrukcije koja je u sukobu sa zdravim razumom". Radi se o "krivulji" (neprekidnom preslikavanju sa segmenta) čija je slika cijeli jedinični kvadrat. Dakle, ne samo da jedinični segment ima jednako "individualnih" točaka kao i jedinični kvadrat (što je relativno lako, i u uskoj vezi s ovim što sam gore pričao o ekvipotentnosti |R i |C ), nego se segment može "smotati", zadržavajući svoj kontinuitet, tako da zaista prekrije cijeli kvadrat. :-)
[quote][quote]Wrong. U onom linku koji sam ti dao, odskrolaj koji ekran gore, do onog "No cat has eight tails.". Ovo je jezička pogreška.[/quote]
mozda sam dosadan, zar nije ta tvrdnja matematicki ispravna?! bez obzira sto nismo definirali nista, odnosno ako definiramo nista kao svojstvo praznog skupa?[/quote]
[quote]dobro...a sto ako nista definiramo kao svojstvo praznog skupa?! u tom slucaju, prazan skup je stvarno prazan, tj. njegovo svojstvo je da sadrzi nista. kao sto, recimo, za skup N definiramo prvi element i uvjet kako se sljedeci elementi pojavljuju.[/quote]
Razlikuj "svojstvo" (definirajuće svojstvo, u ovom slučaju) od "elemenata". Nadam se da je cinikova "prazna filozofija" ovdje pomogla.
| HijenA (napisa): | | ...jer je mislio da je nemoguce prebrojati beskonacne skupove. sta ako ih ima beskonacno (neprebrojivo) mnogo?! |
Izraz "neprebrojiv" se definira kao "ima više elemenata od skupa \N ", i nema baš puno veze s "brojanjem" kako se ono obično shvaća. O tome je već bilo govora po Forumu, npr. http://degiorgi.math.hr/forum/viewtopic.php?t=2465 .
Inače, Cantor je (s razlogom, u društvu u kojem je živio) bio jako oprezan s beskonačnošću... "infinitno" je bilo i iz njegove perspektive Božje, nedohvatljivo ljudima (i označavalo nešto što bismo danas zvali pravim klasama), dok se on bavio samo "_trans_finitnim", dakle onim što je "malo veće od konačnog" (ali još uvijek ljudskom umu dokučivo).
| Citat: | | da, svaki hotel ima beskonacno mnogo soba, a hotela ima beskonacno mnogo. |
Ali samo to za problem nije dovoljno - treba ih biti prebrojivo mnogo. Bar ovaj gornji dokaz prolazi samo za prebrojive skupove.
| Citat: | | dobro...to sam shvatio. ako su prebrojivi. a to je veliko ako. a sto ako nisu prebrojivi?! onda znaci da ne postoji ta bijekcija?! |
Možda postoji. No za to nam trebaju jače pretpostavke.
Npr. ako prihvatimo nešto što se zove ZFC (standardna teorija skupova s _aksiomom izbora_), izlazi da je svaki beskonačni kardinalni broj ekvipotentan sa svojim kvadratom. Dakle, ne samo da |Nx|N ima jednako mnogo elemenata kao |N , već bilo koji beskonačni skup S ima jednako mnogo elemenata kao SxS .
Za mnoge "konkretne" skupove, however, puni ZFC nam ipak ne treba - npr. već u ZF se može vidjeti da je |Rx|R ekvipotentan s |R - kompleksnih brojeva ima jednako koliko i realnih.
| Citat: | | jer, recimo, skup R je beskonacno neprebrojiv jer izmedju svakog realnog broja postoji beskonacno mnogo realnih brojeva bez obzira koliko oni bili mali. |
A bunch of parse errors... :-/
no što god da si htio reći, čini mi se da isto vrijedi i za |Q , a |Q je prebrojiv. Gustoća uređaja nema puno veze s potpunošću.
No kao što rekoh gore, vrijedi analogna tvrdnja i za |R - ako imaš kontinuum hotelâ, i u svakom od njih kontinuum sobâ, tada i ukupno imaš kontinuum sobâ.
| Citat: | | znaci, kad bi skup {1,2,3} izgledao {1,2,3,1,2,3}, iako je to nemoguce, |
Ovisi. Što se mene tiče, {1,2,3,1,2,3} je samo drugi, čudniji, zapis za {1,2,3} (kao što je npr. 34/51 drugi, čudniji zapis za 2/3 ). Postoje ljudi koji smatraju {1,2,3,1,2,3} ilegalnom oznakom za skup, no takvi ljudi IME obično nisu svjesni da ih to sprečava npr. govoriti o skupu {a,b} ako nisu sigurni da je a != b ... [ ] ]
| Citat: | | onda bi on bio element samog sebe, rajt?! |
Ne. I dalje su njegovi elementi samo 1 , 2 i 3 , a ne S .
| Citat: | | a sto se tice praznog skupa...ako definiramo prazan skup kao { x | x!=x }, onda nista nije element tog skupa. medjutim, ako ga definiramo kao 0={} onda nista jest element tog skupa jer se izmedju zagrada nalazi nista, a onda je nista element. to meni nikako nije jasno. |
Niti meni. Kao što rekoh, "ništa" nije matematički pojam. To je samo fraza u hrvatskom jeziku kojom se nešto opisuje (i vodi do čudnih dvoznačnosti, poput ovog gore). Budući da math-jezik to može puno preciznije opisati, kvantifikatorima, njemu pojam "ništa" (u ovom kontekstu) ne treba.
Ti možeš reći "ništa nije element od 0 ", ako definiraš da ti to znači 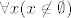 . Također možeš reći i "ništa jest element od 0 ", ako definiraš da ti _to_ znači . Također možeš reći i "ništa jest element od 0 ", ako definiraš da ti _to_ znači 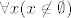 . But you can't have it both ways. Stvar je samo u hrvatskom jeziku, i u njegovom čudnom shvaćanju dvostruke negacije. . But you can't have it both ways. Stvar je samo u hrvatskom jeziku, i u njegovom čudnom shvaćanju dvostruke negacije.
| Citat: | | Citat: | | štoviše, u ZF , standardnoj teoriji skupova, nijedan skup nije element samog sebe. |
da...pa to je samo po sebi jasno. |
Ne mora biti... postoje teorije vrlo slične standardnoj teoriji skupova, npr. ZFA , u kojima to eksplicitno ne vrijedi - _postoji_ skup koji je element samog sebe.
| FMB (napisa): | | nije moguce da skup bude element samog sebe. Zasto? Zato jer ako to dozvolimo, za posljedicu cemo dobiti paradokse i kontradikcije u teoriji. |
Nećemo. 
Možda zanimljivije, pretpostavka o utemeljenosti (ie, da nema "ciklusa" u relaciji "biti element") zapravo _nije_ essentially potrebna (iako je psihološki nesumnjivo lakše s njom raditi teoriju skupova) - može se dokazati da u teoriji ZF-Foundation postoji unutrašnji model (relativni dokaz konzistentnosti) kompletne teorije ZF . Skica dokaza: izgrade se (wellfounded) ordinali, i preko njih i partitivnog skupa, cijela kumulativna hijerarhija. Pokaže se da ona pokupi upravo ono što treba - cijeli ZF vrijedi unutar nje, a svi "loši" skupovi (koji nisu dobro utemeljeni relacijom @ ) ostanu vani.
Slučajno znam jer ima veze s mojim magistarskim. 
| Citat: | | Citat: | | http://www.cut-the-knot.org/do_you_know/hilbert.shtml |
malo sam mutav danas...please explain  |
Peanova krivulja se valjda navodi kao standardni primjer "logičke konstrukcije koja je u sukobu sa zdravim razumom". Radi se o "krivulji" (neprekidnom preslikavanju sa segmenta) čija je slika cijeli jedinični kvadrat. Dakle, ne samo da jedinični segment ima jednako "individualnih" točaka kao i jedinični kvadrat (što je relativno lako, i u uskoj vezi s ovim što sam gore pričao o ekvipotentnosti |R i |C ), nego se segment može "smotati", zadržavajući svoj kontinuitet, tako da zaista prekrije cijeli kvadrat. 
| Citat: | | Citat: | | Wrong. U onom linku koji sam ti dao, odskrolaj koji ekran gore, do onog "No cat has eight tails.". Ovo je jezička pogreška. |
mozda sam dosadan, zar nije ta tvrdnja matematicki ispravna?! bez obzira sto nismo definirali nista, odnosno ako definiramo nista kao svojstvo praznog skupa? |
| Citat: | | dobro...a sto ako nista definiramo kao svojstvo praznog skupa?! u tom slucaju, prazan skup je stvarno prazan, tj. njegovo svojstvo je da sadrzi nista. kao sto, recimo, za skup N definiramo prvi element i uvjet kako se sljedeci elementi pojavljuju. |
Razlikuj "svojstvo" (definirajuće svojstvo, u ovom slučaju) od "elemenata". Nadam se da je cinikova "prazna filozofija" ovdje pomogla.
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 1:02 čet, 11. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova Postano: 1:02 čet, 11. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova |
    |
|
|
[quote="veky"][quote="HijenA"]...jer je mislio da je nemoguce prebrojati beskonacne skupove. sta ako ih ima beskonacno (neprebrojivo) mnogo?![/quote]
Izraz "neprebrojiv" se definira kao "ima više elemenata od skupa \N ", i nema baš puno veze s "brojanjem" kako se ono obično shvaća. O tome je već bilo govora po Forumu, npr. http://degiorgi.math.hr/forum/viewtopic.php?t=2465 .
Inače, Cantor je (s razlogom, u društvu u kojem je živio) bio jako oprezan s beskonačnošću... "infinitno" je bilo i iz njegove perspektive Božje, nedohvatljivo ljudima (i označavalo nešto što bismo danas zvali pravim klasama), dok se on bavio samo "_trans_finitnim", dakle onim što je "malo veće od konačnog" (ali još uvijek ljudskom umu dokučivo).[/quote]
nije to samo karakteristicno za Cantorovo vrijeme, to se vrlo lako moze preslikati i danas jer jos uvijek ima ljudi koji su zarobljeni u dogmama proslosti, bilo religijskim, bilo filozofskim. tu mi nazalost ne mozemo pomoci.
[quote]
[quote]da, svaki hotel ima beskonacno mnogo soba, a hotela ima beskonacno mnogo.[/quote]
Ali samo to za problem nije dovoljno - treba ih biti prebrojivo mnogo. Bar ovaj gornji dokaz prolazi samo za prebrojive skupove.[/quote]
sad cu ponovit pitanje odozgora, valjda me nece netko ispljuvat [;)]: dakle, sto ako imamo skupove koje ne mozemo izbrojati?!
[quote]
[quote]dobro...to sam shvatio. ako su prebrojivi. a to je veliko ako. a sto ako nisu prebrojivi?! onda znaci da ne postoji ta bijekcija?![/quote]
Možda postoji. No za to nam trebaju jače pretpostavke.[/quote]
vidi gore. sto ako imamo skup koji nije prebrojiv (kao recimo skup |N)? pretpostavimo da imamo skup koji nije prebrojiv. u analizi 1 smo radi Cantor-Bernsteinov teorem koji kaze da je neki skup S ekvipotentan sa |N ako se izmedju njih moze konstruirati bijekcija. tada oni imaju iste kardinalne brojeve, odnosno S=|N. medjutim, taj teorem za skup |R ne vrijedi. sto ako imamo takav slucaj?! kako je moguce da jedna pretpostavka vrijedi samo za jedan slucaj, a ne za vise njih?
[quote]
Npr. ako prihvatimo nešto što se zove ZFC (standardna teorija skupova s _aksiomom izbora_), izlazi da je svaki beskonačni kardinalni broj ekvipotentan sa svojim kvadratom. Dakle, ne samo da |Nx|N ima jednako mnogo elemenata kao |N , već bilo koji beskonačni skup S ima jednako mnogo elemenata kao SxS .
Za mnoge "konkretne" skupove, however, puni ZFC nam ipak ne treba - npr. već u ZF se može vidjeti da je |Rx|R ekvipotentan s |R - kompleksnih brojeva ima jednako koliko i realnih.[/quote]
recimo da sam shvatio ovaj dio.
[quote]
[quote] jer, recimo, skup R je beskonacno neprebrojiv jer izmedju svakog realnog broja postoji beskonacno mnogo realnih brojeva bez obzira koliko oni bili mali.[/quote]
A bunch of parse errors... :-/
no što god da si htio reći, čini mi se da isto vrijedi i za |Q , a |Q je prebrojiv. Gustoća uređaja nema puno veze s potpunošću.[/quote]
evo sto sam tocno htio reci (upravo sam nasao materijale sa predavanja sa analize 1 :) ):
[b]Propozicija:[/b]
Za svaki a, b e |R, a < b, segment [a,b] je neprebrojiv skup.
[b]Korolar:[/b]
|R je neprebrojiv skup.
sad, da ne pisem dokaz ova dva teorema...ako je neki skup koji je podskup od |R neprebrojiv, onda je i on sam neprebrojiv.
[quote]
No kao što rekoh gore, vrijedi analogna tvrdnja i za |R - ako imaš kontinuum hotelâ, i u svakom od njih kontinuum sobâ, tada i ukupno imaš kontinuum sobâ.[/quote]
yup...to je jasno.
[quote]
[quote]znaci, kad bi skup {1,2,3} izgledao {1,2,3,1,2,3}, iako je to nemoguce,[/quote]
Ovisi. Što se mene tiče, {1,2,3,1,2,3} je samo drugi, čudniji, zapis za {1,2,3} (kao što je npr. 34/51 drugi, čudniji zapis za 2/3 ). Postoje ljudi koji smatraju {1,2,3,1,2,3} ilegalnom oznakom za skup, no takvi ljudi IME obično nisu svjesni da ih to sprečava npr. govoriti o skupu {a,b} ako nisu sigurni da je a != b ... [:-P][/quote]
ne...mislio sam da isti skup sadrzi 2 ista elementa...znaci {1,2,3,1,2,3}, ova zadnja 3 broja su clanovi skupa sami za sebe, nisu ni u kakvoj vezi sa prva 3 clana.
[quote]
[quote] onda bi on bio element samog sebe, rajt?![/quote]
Ne. I dalje su njegovi elementi samo 1 , 2 i 3 , a ne S .[/quote]
to sam shvatio danas popodne...no sto je u ovom slucaju: S={1,2,3,S}
da li je on onda sadrzan u samome sebi? ili recimo {1,2,3,{1,2,3}}
[quote]
[quote] a sto se tice praznog skupa...ako definiramo prazan skup kao { x | x!=x }, onda nista nije element tog skupa. medjutim, ako ga definiramo kao 0={} onda nista jest element tog skupa jer se izmedju zagrada nalazi nista, a onda je nista element. to meni nikako nije jasno.[/quote]
Niti meni. Kao što rekoh, "ništa" nije matematički pojam. To je samo fraza u hrvatskom jeziku kojom se nešto opisuje (i vodi do čudnih dvoznačnosti, poput ovog gore). Budući da math-jezik to može puno preciznije opisati, kvantifikatorima, njemu pojam "ništa" (u ovom kontekstu) ne treba.
Ti možeš reći "ništa nije element od 0 ", ako definiraš da ti to znači [latex]\forall x(x\not\in\emptyset)[/latex]. Također možeš reći i "ništa jest element od 0 ", ako definiraš da ti _to_ znači [latex]\forall x(x\not\in\emptyset)[/latex]. But you can't have it both ways. Stvar je samo u hrvatskom jeziku, i u njegovom čudnom shvaćanju dvostruke negacije.[/quote]
thanx na razjasnjenju.
[quote][quote][quote]štoviše, u ZF , standardnoj teoriji skupova, nijedan skup nije element samog sebe.[/quote]
da...pa to je samo po sebi jasno.[/quote]
Ne mora biti... postoje teorije vrlo slične standardnoj teoriji skupova, npr. ZFA , u kojima to eksplicitno ne vrijedi - _postoji_ skup koji je element samog sebe.[/quote]
nisi li sad u kontradikciji sa samim sobom?! do sad si tvrdio da ne postoji skup koji je element samog sebe. a sad taj skup ipak postoji (to je bila i moja pocetna premisa, premda zasnovana na krivim pretpostavkama). koji je to skup?
[quote][quote][quote]http://www.cut-the-knot.org/do_you_know/hilbert.shtml[/quote]
malo sam mutav danas...please explain ;)[/quote]
Peanova krivulja se valjda navodi kao standardni primjer "logičke konstrukcije koja je u sukobu sa zdravim razumom". Radi se o "krivulji" (neprekidnom preslikavanju sa segmenta) čija je slika cijeli jedinični kvadrat. Dakle, ne samo da jedinični segment ima jednako "individualnih" točaka kao i jedinični kvadrat (što je relativno lako, i u uskoj vezi s ovim što sam gore pričao o ekvipotentnosti |R i |C ), nego se segment može "smotati", zadržavajući svoj kontinuitet, tako da zaista prekrije cijeli kvadrat. :-)[quote]
jos jedno potpitanje (malo sam spavao nocas [size=9]gledao gospodara prstenova pa ne mogu razmisljat :D[/size]), sto je to jedinicni kvadrat? jel to isto kao i jedinicna kruznica (radijus je 1), pa prema tome, stranica kvadrata bi trebala biti 1, rajt?! :)
[quote]
[quote][quote]Wrong. U onom linku koji sam ti dao, odskrolaj koji ekran gore, do onog "No cat has eight tails.". Ovo je jezička pogreška.[/quote]
mozda sam dosadan, zar nije ta tvrdnja matematicki ispravna?! bez obzira sto nismo definirali nista, odnosno ako definiramo nista kao svojstvo praznog skupa?[/quote]
[quote]dobro...a sto ako nista definiramo kao svojstvo praznog skupa?! u tom slucaju, prazan skup je stvarno prazan, tj. njegovo svojstvo je da sadrzi nista. kao sto, recimo, za skup N definiramo prvi element i uvjet kako se sljedeci elementi pojavljuju.[/quote]
Razlikuj "svojstvo" (definirajuće svojstvo, u ovom slučaju) od "elemenata". Nadam se da je cinikova "prazna filozofija" ovdje pomogla.[/quote]
jest...ova tvoja zadnja recenica pokazuje da smo mislili istu stvar. znaci, matematicki, nistavilo se definira kao: za svaki x [latex]x\neq x[/latex] a to nije element vec svojstvo praznog skupa. opet, ispravi me ako grijesim.
| veky (napisa): | | HijenA (napisa): | | ...jer je mislio da je nemoguce prebrojati beskonacne skupove. sta ako ih ima beskonacno (neprebrojivo) mnogo?! |
Izraz "neprebrojiv" se definira kao "ima više elemenata od skupa \N ", i nema baš puno veze s "brojanjem" kako se ono obično shvaća. O tome je već bilo govora po Forumu, npr. http://degiorgi.math.hr/forum/viewtopic.php?t=2465 .
Inače, Cantor je (s razlogom, u društvu u kojem je živio) bio jako oprezan s beskonačnošću... "infinitno" je bilo i iz njegove perspektive Božje, nedohvatljivo ljudima (i označavalo nešto što bismo danas zvali pravim klasama), dok se on bavio samo "_trans_finitnim", dakle onim što je "malo veće od konačnog" (ali još uvijek ljudskom umu dokučivo). |
nije to samo karakteristicno za Cantorovo vrijeme, to se vrlo lako moze preslikati i danas jer jos uvijek ima ljudi koji su zarobljeni u dogmama proslosti, bilo religijskim, bilo filozofskim. tu mi nazalost ne mozemo pomoci.
| Citat: |
| Citat: | | da, svaki hotel ima beskonacno mnogo soba, a hotela ima beskonacno mnogo. |
Ali samo to za problem nije dovoljno - treba ih biti prebrojivo mnogo. Bar ovaj gornji dokaz prolazi samo za prebrojive skupove. |
sad cu ponovit pitanje odozgora, valjda me nece netko ispljuvat [ ]: dakle, sto ako imamo skupove koje ne mozemo izbrojati?! ]: dakle, sto ako imamo skupove koje ne mozemo izbrojati?!
| Citat: |
| Citat: | | dobro...to sam shvatio. ako su prebrojivi. a to je veliko ako. a sto ako nisu prebrojivi?! onda znaci da ne postoji ta bijekcija?! |
Možda postoji. No za to nam trebaju jače pretpostavke. |
vidi gore. sto ako imamo skup koji nije prebrojiv (kao recimo skup |N)? pretpostavimo da imamo skup koji nije prebrojiv. u analizi 1 smo radi Cantor-Bernsteinov teorem koji kaze da je neki skup S ekvipotentan sa |N ako se izmedju njih moze konstruirati bijekcija. tada oni imaju iste kardinalne brojeve, odnosno S=|N. medjutim, taj teorem za skup |R ne vrijedi. sto ako imamo takav slucaj?! kako je moguce da jedna pretpostavka vrijedi samo za jedan slucaj, a ne za vise njih?
| Citat: |
Npr. ako prihvatimo nešto što se zove ZFC (standardna teorija skupova s _aksiomom izbora_), izlazi da je svaki beskonačni kardinalni broj ekvipotentan sa svojim kvadratom. Dakle, ne samo da |Nx|N ima jednako mnogo elemenata kao |N , već bilo koji beskonačni skup S ima jednako mnogo elemenata kao SxS .
Za mnoge "konkretne" skupove, however, puni ZFC nam ipak ne treba - npr. već u ZF se može vidjeti da je |Rx|R ekvipotentan s |R - kompleksnih brojeva ima jednako koliko i realnih. |
recimo da sam shvatio ovaj dio.
| Citat: |
| Citat: | | jer, recimo, skup R je beskonacno neprebrojiv jer izmedju svakog realnog broja postoji beskonacno mnogo realnih brojeva bez obzira koliko oni bili mali. |
A bunch of parse errors... :-/
no što god da si htio reći, čini mi se da isto vrijedi i za |Q , a |Q je prebrojiv. Gustoća uređaja nema puno veze s potpunošću. |
evo sto sam tocno htio reci (upravo sam nasao materijale sa predavanja sa analize 1  ): ):
Propozicija:
Za svaki a, b e |R, a < b, segment [a,b] je neprebrojiv skup.
Korolar:
|R je neprebrojiv skup.
sad, da ne pisem dokaz ova dva teorema...ako je neki skup koji je podskup od |R neprebrojiv, onda je i on sam neprebrojiv.
| Citat: |
No kao što rekoh gore, vrijedi analogna tvrdnja i za |R - ako imaš kontinuum hotelâ, i u svakom od njih kontinuum sobâ, tada i ukupno imaš kontinuum sobâ. |
yup...to je jasno.
| Citat: |
| Citat: | | znaci, kad bi skup {1,2,3} izgledao {1,2,3,1,2,3}, iako je to nemoguce, |
Ovisi. Što se mene tiče, {1,2,3,1,2,3} je samo drugi, čudniji, zapis za {1,2,3} (kao što je npr. 34/51 drugi, čudniji zapis za 2/3 ). Postoje ljudi koji smatraju {1,2,3,1,2,3} ilegalnom oznakom za skup, no takvi ljudi IME obično nisu svjesni da ih to sprečava npr. govoriti o skupu {a,b} ako nisu sigurni da je a != b ... [ ] ] |
ne...mislio sam da isti skup sadrzi 2 ista elementa...znaci {1,2,3,1,2,3}, ova zadnja 3 broja su clanovi skupa sami za sebe, nisu ni u kakvoj vezi sa prva 3 clana.
| Citat: |
| Citat: | | onda bi on bio element samog sebe, rajt?! |
Ne. I dalje su njegovi elementi samo 1 , 2 i 3 , a ne S . |
to sam shvatio danas popodne...no sto je u ovom slucaju: S={1,2,3,S}
da li je on onda sadrzan u samome sebi? ili recimo {1,2,3,{1,2,3}}
| Citat: |
| Citat: | | a sto se tice praznog skupa...ako definiramo prazan skup kao { x | x!=x }, onda nista nije element tog skupa. medjutim, ako ga definiramo kao 0={} onda nista jest element tog skupa jer se izmedju zagrada nalazi nista, a onda je nista element. to meni nikako nije jasno. |
Niti meni. Kao što rekoh, "ništa" nije matematički pojam. To je samo fraza u hrvatskom jeziku kojom se nešto opisuje (i vodi do čudnih dvoznačnosti, poput ovog gore). Budući da math-jezik to može puno preciznije opisati, kvantifikatorima, njemu pojam "ništa" (u ovom kontekstu) ne treba.
Ti možeš reći "ništa nije element od 0 ", ako definiraš da ti to znači 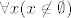 . Također možeš reći i "ništa jest element od 0 ", ako definiraš da ti _to_ znači . Također možeš reći i "ništa jest element od 0 ", ako definiraš da ti _to_ znači 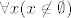 . But you can't have it both ways. Stvar je samo u hrvatskom jeziku, i u njegovom čudnom shvaćanju dvostruke negacije. . But you can't have it both ways. Stvar je samo u hrvatskom jeziku, i u njegovom čudnom shvaćanju dvostruke negacije. |
thanx na razjasnjenju.
| Citat: | | Citat: | | Citat: | | štoviše, u ZF , standardnoj teoriji skupova, nijedan skup nije element samog sebe. |
da...pa to je samo po sebi jasno. |
Ne mora biti... postoje teorije vrlo slične standardnoj teoriji skupova, npr. ZFA , u kojima to eksplicitno ne vrijedi - _postoji_ skup koji je element samog sebe. |
nisi li sad u kontradikciji sa samim sobom?! do sad si tvrdio da ne postoji skup koji je element samog sebe. a sad taj skup ipak postoji (to je bila i moja pocetna premisa, premda zasnovana na krivim pretpostavkama). koji je to skup?
[quote] | Citat: | | Citat: | | http://www.cut-the-knot.org/do_you_know/hilbert.shtml |
malo sam mutav danas...please explain  |
Peanova krivulja se valjda navodi kao standardni primjer "logičke konstrukcije koja je u sukobu sa zdravim razumom". Radi se o "krivulji" (neprekidnom preslikavanju sa segmenta) čija je slika cijeli jedinični kvadrat. Dakle, ne samo da jedinični segment ima jednako "individualnih" točaka kao i jedinični kvadrat (što je relativno lako, i u uskoj vezi s ovim što sam gore pričao o ekvipotentnosti |R i |C ), nego se segment može "smotati", zadržavajući svoj kontinuitet, tako da zaista prekrije cijeli kvadrat.  [quote] [quote]
jos jedno potpitanje (malo sam spavao nocas gledao gospodara prstenova pa ne mogu razmisljat  ), sto je to jedinicni kvadrat? jel to isto kao i jedinicna kruznica (radijus je 1), pa prema tome, stranica kvadrata bi trebala biti 1, rajt?! ), sto je to jedinicni kvadrat? jel to isto kao i jedinicna kruznica (radijus je 1), pa prema tome, stranica kvadrata bi trebala biti 1, rajt?! 
| Citat: |
| Citat: | | Citat: | | Wrong. U onom linku koji sam ti dao, odskrolaj koji ekran gore, do onog "No cat has eight tails.". Ovo je jezička pogreška. |
mozda sam dosadan, zar nije ta tvrdnja matematicki ispravna?! bez obzira sto nismo definirali nista, odnosno ako definiramo nista kao svojstvo praznog skupa? |
| Citat: | | dobro...a sto ako nista definiramo kao svojstvo praznog skupa?! u tom slucaju, prazan skup je stvarno prazan, tj. njegovo svojstvo je da sadrzi nista. kao sto, recimo, za skup N definiramo prvi element i uvjet kako se sljedeci elementi pojavljuju. |
Razlikuj "svojstvo" (definirajuće svojstvo, u ovom slučaju) od "elemenata". Nadam se da je cinikova "prazna filozofija" ovdje pomogla. |
jest...ova tvoja zadnja recenica pokazuje da smo mislili istu stvar. znaci, matematicki, nistavilo se definira kao: za svaki x 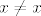 a to nije element vec svojstvo praznog skupa. opet, ispravi me ako grijesim. a to nije element vec svojstvo praznog skupa. opet, ispravi me ako grijesim.
|
|
| [Vrh] |
|
cinik
Forumaš(ica)


Pridružen/a: 27. 04. 2003. (23:34:09)
Postovi: (1FB)16
Spol: 
Lokacija: /proc/sys/cpu/
|
 Postano: 8:50 čet, 11. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova Postano: 8:50 čet, 11. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova |
    |
|
|
[quote="HijenA"][quote="veky"]
Inače, Cantor je (s razlogom, u društvu u kojem je živio) bio jako oprezan s beskonačnošću... "infinitno" je bilo i iz njegove perspektive Božje, nedohvatljivo ljudima (i označavalo nešto što bismo danas zvali pravim klasama), dok se on bavio samo "_trans_finitnim", dakle onim što je "malo veće od konačnog" (ali još uvijek ljudskom umu dokučivo).[/quote]
nije to samo karakteristicno za Cantorovo vrijeme, to se vrlo lako moze preslikati i danas jer jos uvijek ima ljudi koji su zarobljeni u dogmama proslosti, bilo religijskim, bilo filozofskim. tu mi nazalost ne mozemo pomoci.
[/quote]
ako se bolje razmisli, rijec i ideja transfinitnosti je puno precizniji opis stanja od beskonacnosti. Prijevod bi bio natkonacni skupovi, a to bolje pase u intuiciju za poimanje nepostojanja skupa svih skupova.
[quote][quote]
[quote]da, svaki hotel ima beskonacno mnogo soba, a hotela ima beskonacno mnogo.[/quote]
Ali samo to za problem nije dovoljno - treba ih biti prebrojivo mnogo. Bar ovaj gornji dokaz prolazi samo za prebrojive skupove.[/quote]
sad cu ponovit pitanje odozgora, valjda me nece netko ispljuvat [;)]: dakle, sto ako imamo skupove koje ne mozemo izbrojati?[/quote]
Citaj sta ti je veky rekao -- prebrojivost skupa nema nikakve veze sa brojanjem i izbrojavanjem.
[quote]
[quote]
[quote] jer, recimo, skup R je beskonacno neprebrojiv jer izmedju svakog realnog broja postoji beskonacno mnogo realnih brojeva bez obzira koliko oni bili mali.[/quote]
A bunch of parse errors... :-/
no što god da si htio reći, čini mi se da isto vrijedi i za |Q , a |Q je prebrojiv. Gustoća uređaja nema puno veze s potpunošću.[/quote]
evo sto sam tocno htio reci (upravo sam nasao materijale sa predavanja sa analize 1 :) ):
[b]Propozicija:[/b]
Za svaki a, b e |R, a < b, segment [a,b] je neprebrojiv skup.
[b]Korolar:[/b]
|R je neprebrojiv skup.
sad, da ne pisem dokaz ova dva teorema...ako je neki skup koji je podskup od |R neprebrojiv, onda je i on sam neprebrojiv.
[/quote]
WRONG!
Pise da je svaki segment neprebrojiv -- segment je "puna crta" sa svim tockama -- racionalnim i iracionalnim izmedju dvije tocke. Definicija prebrojivosti kaze da je |N prebrojiv, a ispada i da je Q prebrojiv. Prebrojivost bi bila mogucnost da se skace s jednog elementa na drugi, i to tako da se do svakog pojedinog elementa moze u konacnom (ne bas nuzno kratkom) vremenu moze doci do bilo kojeg elementa skacuci jedan po jedan.
Uzmimo neki prirodan broj n. Do njega dodjes tako da brojis 1,2,3,4,5,.... ako je broj n=10^{10^{10}} to brojanje ce malo potrajati, ali ces doci do njega (ili vec neki tvoj potomak).
[quote]
ne...mislio sam da isti skup sadrzi 2 ista elementa...znaci {1,2,3,1,2,3}, ova zadnja 3 broja su clanovi skupa sami za sebe, nisu ni u kakvoj vezi sa prva 3 clana.
[/quote]
1=1, pa je zato {1,1}={1}, pa jesu u nekakvoj vezi pa je izrecena tvrdnja glupost.
[quote]
to sam shvatio danas popodne...no sto je u ovom slucaju: S={1,2,3,S}
da li je on onda sadrzan u samome sebi? ili recimo {1,2,3,{1,2,3}}
[/quote]
Vidi gore moj primjer. {1,2,3} NIJE element od {1,2,3}, pa NIJE ELEMENT od samoga sebe. S:={1,2,3,S} jest element od samoga sebe, no S!={1,2,3,{1,2,3}}. S ti izgleda ovako nekako {1,2,3,{1,2,3,{1,2,3,{1,2,3,{1,2,3,S}}}}.
Pa je opet S u tome duuuuugacak i tako u natkonacnost :)
'ave fun!
Sinisa
| HijenA (napisa): | | veky (napisa): |
Inače, Cantor je (s razlogom, u društvu u kojem je živio) bio jako oprezan s beskonačnošću... "infinitno" je bilo i iz njegove perspektive Božje, nedohvatljivo ljudima (i označavalo nešto što bismo danas zvali pravim klasama), dok se on bavio samo "_trans_finitnim", dakle onim što je "malo veće od konačnog" (ali još uvijek ljudskom umu dokučivo). |
nije to samo karakteristicno za Cantorovo vrijeme, to se vrlo lako moze preslikati i danas jer jos uvijek ima ljudi koji su zarobljeni u dogmama proslosti, bilo religijskim, bilo filozofskim. tu mi nazalost ne mozemo pomoci.
|
ako se bolje razmisli, rijec i ideja transfinitnosti je puno precizniji opis stanja od beskonacnosti. Prijevod bi bio natkonacni skupovi, a to bolje pase u intuiciju za poimanje nepostojanja skupa svih skupova.
| Citat: | | Citat: |
| Citat: | | da, svaki hotel ima beskonacno mnogo soba, a hotela ima beskonacno mnogo. |
Ali samo to za problem nije dovoljno - treba ih biti prebrojivo mnogo. Bar ovaj gornji dokaz prolazi samo za prebrojive skupove. |
sad cu ponovit pitanje odozgora, valjda me nece netko ispljuvat [ ]: dakle, sto ako imamo skupove koje ne mozemo izbrojati? ]: dakle, sto ako imamo skupove koje ne mozemo izbrojati? |
Citaj sta ti je veky rekao – prebrojivost skupa nema nikakve veze sa brojanjem i izbrojavanjem.
| Citat: |
| Citat: |
| Citat: | | jer, recimo, skup R je beskonacno neprebrojiv jer izmedju svakog realnog broja postoji beskonacno mnogo realnih brojeva bez obzira koliko oni bili mali. |
A bunch of parse errors... :-/
no što god da si htio reći, čini mi se da isto vrijedi i za |Q , a |Q je prebrojiv. Gustoća uređaja nema puno veze s potpunošću. |
evo sto sam tocno htio reci (upravo sam nasao materijale sa predavanja sa analize 1  ): ):
Propozicija:
Za svaki a, b e |R, a < b, segment [a,b] je neprebrojiv skup.
Korolar:
|R je neprebrojiv skup.
sad, da ne pisem dokaz ova dva teorema...ako je neki skup koji je podskup od |R neprebrojiv, onda je i on sam neprebrojiv.
|
WRONG!
Pise da je svaki segment neprebrojiv – segment je "puna crta" sa svim tockama – racionalnim i iracionalnim izmedju dvije tocke. Definicija prebrojivosti kaze da je |N prebrojiv, a ispada i da je Q prebrojiv. Prebrojivost bi bila mogucnost da se skace s jednog elementa na drugi, i to tako da se do svakog pojedinog elementa moze u konacnom (ne bas nuzno kratkom) vremenu moze doci do bilo kojeg elementa skacuci jedan po jedan.
Uzmimo neki prirodan broj n. Do njega dodjes tako da brojis 1,2,3,4,5,.... ako je broj n=10^{10^{10}} to brojanje ce malo potrajati, ali ces doci do njega (ili vec neki tvoj potomak).
| Citat: |
ne...mislio sam da isti skup sadrzi 2 ista elementa...znaci {1,2,3,1,2,3}, ova zadnja 3 broja su clanovi skupa sami za sebe, nisu ni u kakvoj vezi sa prva 3 clana.
|
1=1, pa je zato {1,1}={1}, pa jesu u nekakvoj vezi pa je izrecena tvrdnja glupost.
| Citat: |
to sam shvatio danas popodne...no sto je u ovom slucaju: S={1,2,3,S}
da li je on onda sadrzan u samome sebi? ili recimo {1,2,3,{1,2,3}}
|
Vidi gore moj primjer. {1,2,3} NIJE element od {1,2,3}, pa NIJE ELEMENT od samoga sebe. S:={1,2,3,S} jest element od samoga sebe, no S!={1,2,3,{1,2,3}}. S ti izgleda ovako nekako {1,2,3,{1,2,3,{1,2,3,{1,2,3,{1,2,3,S}}}}.
Pa je opet S u tome duuuuugacak i tako u natkonacnost 
'ave fun!
Sinisa
_________________
Oslobodjen Senata.
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 9:45 čet, 11. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova Postano: 9:45 čet, 11. 11. 2004 Naslov: Re: Kantor i paradoxi u teoriji skupova |
    |
|
|
[quote="HijenA"]vidi gore. sto ako imamo skup koji nije prebrojiv (kao recimo skup |N)? [/quote]
Ma vidi ti gore (odnosno dolje: ). Objašnjeno ti je da tvrdnja može vrijediti i općenito za beskonačne skupove (u ZFC), te je navedeno da vrijedi za |R (u ZF). SxS je ekvipotentan s S .
Naravno, to ne znači da je _prebrojiv_. Npr. |R je neprebrojiv, pa je tako i |Rx|R . Ali nema _više_ elemenata od skupa od kojeg smo krenuli ( |R ) - ima jednako. Kvadriranje ne povećava beskonačne kardinale.
[quote]pretpostavimo da imamo skup koji nije prebrojiv.[/quote]
Ne treba pretpostavljati. Znamo da je npr. \P(\N) (partitivni skup skupa prirodnih brojeva) neprebrojiv, po Cantorovom teoremu.
[quote] u analizi 1 smo radi Cantor-Bernsteinov teorem koji kaze da je neki skup S ekvipotentan sa |N ako se izmedju njih moze konstruirati bijekcija.[/quote]
To nije teorem, to je _definicija_ ekvipotentnosti.
Pogotovo nije Cantor-Bernsteinov teorem. On kaže da postoji bijekcija _ako i samo ako_ postoje injekcije u oba smjera.
[quote] tada oni imaju iste kardinalne brojeve, odnosno S=|N.[/quote]
Valjda cardS=card|N . I ni to nije teorem, već (na neki način) definicija kardinalnog broja (preciznije, definicija ekvivalencije "imati isti kardinalni broj").
[quote] medjutim, taj teorem za skup |R ne vrijedi.[/quote]
Ako teorem vrijedi u ZF , onda vrijedi za sve skupove :!: . U ovom slučaju, |R jednostavno ne zadovoljava pretpostavku "teorema" (ie, definiciju prebrojivosti), pa nije prebrojiv.
[quote] sto ako imamo takav slucaj?! kako je moguce da jedna pretpostavka vrijedi samo za jedan slucaj, a ne za vise njih?[/quote]
Cijela gužva je IMHO nastala iz toga što nisi dovoljno precizno napisao početni zadatak. Naravno, ako tvrdnja glasi (uz gornje oznake H za skup hotelâ, s_h za skup sobâ hotela h , te S:=U_h@H s_h skup svih sobâ ukupno)
"H beskonačan & svaki s_h beskonačan => S beskonačan",
onda ona vrijedi (trivijalno - H ima bar jedan element, h0 , s_h0 C= S je beskonačan, pa je i S beskonačan).
Ako glasi
"H prebrojiv & svaki s_h prebrojiv => S prebrojiv",
onda također vrijedi, dokaz je ovo što je mdoko napisao (i ja dopunio).
(*)Ako glasi
"H kontinuum & svaki s_h kontinuum => S kontinuum",
opet vrijedi, dokaz ti mogu napisati ako želiš.
Ako glasi
"H beskonačan kardinaliteta kappa & svaki s_h beskonačan kardinaliteta kappa => S beskonačan kardinaliteta kappa",
vrijedi, ali pod većim pretpostavkama - u ZFC . Dokaz ćeš, nadam se, čuti na trećoj godini. (Franka, jel se još radi ovo?)
No ako glasi striktno
"H beskonačan & svi s_h jednakog beskonačnog kardinaliteta => S prebrojiv",
kao što si ti napisao, onda ne vrijedi - kontraprimjer se može direktno očitati iz tvrdnje [*].
[quote][quote]
No kao što rekoh gore, vrijedi analogna tvrdnja i za |R - ako imaš kontinuum hotelâ, i u svakom od njih kontinuum sobâ, tada i ukupno imaš kontinuum sobâ.[/quote]
yup...to je jasno.[/quote]
Do koje mjere jasno? Ako misliš da ti je potpuno jasno, probaj dokazati. ;-)
[quote]ne...mislio sam da isti skup sadrzi 2 ista elementa...znaci {1,2,3,1,2,3}, ova zadnja 3 broja su clanovi skupa sami za sebe, nisu ni u kakvoj vezi sa prva 3 clana.[/quote]
?
Koncept skupa ne dozvoljava nikakvo dodatno atribuiranje relaciji "biti element" (zato i jest tako jednostavan da nosi fundaciju čitave matematike). There's no such thing as "element skupa sam za sebe". Za svaki S , za svaki x , ili je x@S , ili je x(!@)S . I S je s tim informacijama potpuno određen.
[quote]no sto je u ovom slucaju: S={1,2,3,S}
da li je on onda sadrzan u samome sebi?[/quote]
Ovaj jest.
[quote] ili recimo {1,2,3,{1,2,3}}[/quote]
Ovaj nije.
Njegovi elementi su 1 , 2 , 3 i {1,2,3} - ukupno četiri elementa, nijedan od kojih nije {1,2,3,{1,2,3}} .
[quote=HijenA ((Nesi, sorry na dubini kvotanja))][quote][quote][quote]štoviše, u ZF , standardnoj teoriji skupova, nijedan skup nije element samog sebe.[/quote]
da...pa to je samo po sebi jasno.[/quote]
Ne mora biti... postoje teorije vrlo slične standardnoj teoriji skupova, npr. ZFA , u kojima to eksplicitno ne vrijedi - _postoji_ skup koji je element samog sebe.[/quote]
nisi li sad u kontradikciji sa samim sobom?![/quote]
Nisam, ako dovoljno pažljivo čitaš što pišem.
[quote] do sad si tvrdio da ne postoji skup koji je element samog sebe. a sad taj skup ipak postoji (to je bila i moja pocetna premisa, premda zasnovana na krivim pretpostavkama).[/quote]
Sve ovisi o teoriji u kojoj se radi. Postoji _standardna_ teorija skupova, ZF (neki u to stavljaju i aksiom izbora, dakle ZFC ), u kojoj se obično radi ako se ne kaže drugačije. I u njoj zaista ne postoji skup koji je element samog sebe.
No htjedoh samo reći da to nije "samo po sebi jasno", odnosno treba nam specijalan, nezavisan, aksiom samo za tu tvrdnju - moguće je izgraditi alternativne teorije, npr. ZFA, u kojima takav skup postoji, a i dalje je moguće razvijati unutra "običnu" teoriju skupova. Slično kao što u standardnoj, euklidskoj, geometriji točkom izvan pravca postoji samo jedan pravac paralelan s njime, ali se može izgraditi alternativna geometrija u kojoj to ne vrijedi, a svejedno ostali aksiomi vrijede i dobar dio "obične" geometrije može se raditi i tamo.
[quote] koji je to skup?[/quote]
Npr. Om:={Om} , odnosno najmanja fiksna točka formule v@v .
[quote]jos jedno potpitanje (malo sam spavao nocas [size=9]gledao gospodara prstenova pa ne mogu razmisljat :D[/size]), sto je to jedinicni kvadrat? jel to isto kao i jedinicna kruznica (radijus je 1), pa prema tome, stranica kvadrata bi trebala biti 1, rajt?! :)[/quote]
Da. Iako je za gornju svrhu zapravo svejedno - ako se krivuljom može pokriti jedinični kvadrat, onda očito može i bilo koji drugi.
| HijenA (napisa): | | vidi gore. sto ako imamo skup koji nije prebrojiv (kao recimo skup |N)? |
Ma vidi ti gore (odnosno dolje: ). Objašnjeno ti je da tvrdnja može vrijediti i općenito za beskonačne skupove (u ZFC), te je navedeno da vrijedi za |R (u ZF). SxS je ekvipotentan s S .
Naravno, to ne znači da je _prebrojiv_. Npr. |R je neprebrojiv, pa je tako i |Rx|R . Ali nema _više_ elemenata od skupa od kojeg smo krenuli ( |R ) - ima jednako. Kvadriranje ne povećava beskonačne kardinale.
| Citat: | | pretpostavimo da imamo skup koji nije prebrojiv. |
Ne treba pretpostavljati. Znamo da je npr. \P(\N) (partitivni skup skupa prirodnih brojeva) neprebrojiv, po Cantorovom teoremu.
| Citat: | | u analizi 1 smo radi Cantor-Bernsteinov teorem koji kaze da je neki skup S ekvipotentan sa |N ako se izmedju njih moze konstruirati bijekcija. |
To nije teorem, to je _definicija_ ekvipotentnosti.
Pogotovo nije Cantor-Bernsteinov teorem. On kaže da postoji bijekcija _ako i samo ako_ postoje injekcije u oba smjera.
| Citat: | | tada oni imaju iste kardinalne brojeve, odnosno S=|N. |
Valjda cardS=card|N . I ni to nije teorem, već (na neki način) definicija kardinalnog broja (preciznije, definicija ekvivalencije "imati isti kardinalni broj").
| Citat: | | medjutim, taj teorem za skup |R ne vrijedi. |
Ako teorem vrijedi u ZF , onda vrijedi za sve skupove  . U ovom slučaju, |R jednostavno ne zadovoljava pretpostavku "teorema" (ie, definiciju prebrojivosti), pa nije prebrojiv. . U ovom slučaju, |R jednostavno ne zadovoljava pretpostavku "teorema" (ie, definiciju prebrojivosti), pa nije prebrojiv.
| Citat: | | sto ako imamo takav slucaj?! kako je moguce da jedna pretpostavka vrijedi samo za jedan slucaj, a ne za vise njih? |
Cijela gužva je IMHO nastala iz toga što nisi dovoljno precizno napisao početni zadatak. Naravno, ako tvrdnja glasi (uz gornje oznake H za skup hotelâ, s_h za skup sobâ hotela h , te S:=U_h@H s_h skup svih sobâ ukupno)
"H beskonačan & svaki s_h beskonačan ⇒ S beskonačan",
onda ona vrijedi (trivijalno - H ima bar jedan element, h0 , s_h0 C= S je beskonačan, pa je i S beskonačan).
Ako glasi
"H prebrojiv & svaki s_h prebrojiv ⇒ S prebrojiv",
onda također vrijedi, dokaz je ovo što je mdoko napisao (i ja dopunio).
(*)Ako glasi
"H kontinuum & svaki s_h kontinuum ⇒ S kontinuum",
opet vrijedi, dokaz ti mogu napisati ako želiš.
Ako glasi
"H beskonačan kardinaliteta kappa & svaki s_h beskonačan kardinaliteta kappa ⇒ S beskonačan kardinaliteta kappa",
vrijedi, ali pod većim pretpostavkama - u ZFC . Dokaz ćeš, nadam se, čuti na trećoj godini. (Franka, jel se još radi ovo?)
No ako glasi striktno
"H beskonačan & svi s_h jednakog beskonačnog kardinaliteta ⇒ S prebrojiv",
kao što si ti napisao, onda ne vrijedi - kontraprimjer se može direktno očitati iz tvrdnje [*].
| Citat: | | Citat: |
No kao što rekoh gore, vrijedi analogna tvrdnja i za |R - ako imaš kontinuum hotelâ, i u svakom od njih kontinuum sobâ, tada i ukupno imaš kontinuum sobâ. |
yup...to je jasno. |
Do koje mjere jasno? Ako misliš da ti je potpuno jasno, probaj dokazati. 
| Citat: | | ne...mislio sam da isti skup sadrzi 2 ista elementa...znaci {1,2,3,1,2,3}, ova zadnja 3 broja su clanovi skupa sami za sebe, nisu ni u kakvoj vezi sa prva 3 clana. |
?
Koncept skupa ne dozvoljava nikakvo dodatno atribuiranje relaciji "biti element" (zato i jest tako jednostavan da nosi fundaciju čitave matematike). There's no such thing as "element skupa sam za sebe". Za svaki S , za svaki x , ili je x@S , ili je x(!@)S . I S je s tim informacijama potpuno određen.
| Citat: | no sto je u ovom slucaju: S={1,2,3,S}
da li je on onda sadrzan u samome sebi? |
Ovaj jest.
| Citat: | | ili recimo {1,2,3,{1,2,3}} |
Ovaj nije.
Njegovi elementi su 1 , 2 , 3 i {1,2,3} - ukupno četiri elementa, nijedan od kojih nije {1,2,3,{1,2,3}} .
[quote=HijenA ((Nesi, sorry na dubini kvotanja))] | Citat: | | Citat: | | Citat: | | štoviše, u ZF , standardnoj teoriji skupova, nijedan skup nije element samog sebe. |
da...pa to je samo po sebi jasno. |
Ne mora biti... postoje teorije vrlo slične standardnoj teoriji skupova, npr. ZFA , u kojima to eksplicitno ne vrijedi - _postoji_ skup koji je element samog sebe. |
nisi li sad u kontradikciji sa samim sobom?![/quote]
Nisam, ako dovoljno pažljivo čitaš što pišem.
| Citat: | | do sad si tvrdio da ne postoji skup koji je element samog sebe. a sad taj skup ipak postoji (to je bila i moja pocetna premisa, premda zasnovana na krivim pretpostavkama). |
Sve ovisi o teoriji u kojoj se radi. Postoji _standardna_ teorija skupova, ZF (neki u to stavljaju i aksiom izbora, dakle ZFC ), u kojoj se obično radi ako se ne kaže drugačije. I u njoj zaista ne postoji skup koji je element samog sebe.
No htjedoh samo reći da to nije "samo po sebi jasno", odnosno treba nam specijalan, nezavisan, aksiom samo za tu tvrdnju - moguće je izgraditi alternativne teorije, npr. ZFA, u kojima takav skup postoji, a i dalje je moguće razvijati unutra "običnu" teoriju skupova. Slično kao što u standardnoj, euklidskoj, geometriji točkom izvan pravca postoji samo jedan pravac paralelan s njime, ali se može izgraditi alternativna geometrija u kojoj to ne vrijedi, a svejedno ostali aksiomi vrijede i dobar dio "obične" geometrije može se raditi i tamo.
Npr. Om:={Om} , odnosno najmanja fiksna točka formule v@v .
| Citat: | jos jedno potpitanje (malo sam spavao nocas gledao gospodara prstenova pa ne mogu razmisljat  ), sto je to jedinicni kvadrat? jel to isto kao i jedinicna kruznica (radijus je 1), pa prema tome, stranica kvadrata bi trebala biti 1, rajt?! ), sto je to jedinicni kvadrat? jel to isto kao i jedinicna kruznica (radijus je 1), pa prema tome, stranica kvadrata bi trebala biti 1, rajt?!  |
Da. Iako je za gornju svrhu zapravo svejedno - ako se krivuljom može pokriti jedinični kvadrat, onda očito može i bilo koji drugi.
|
|
| [Vrh] |
|
|














