| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Greda
Forumaš(ica)
Pridružen/a: 01. 07. 2006. (14:00:26)
Postovi: (44)16
Spol: 
|
|
| [Vrh] |
|
C
Forumaš(ica)

Pridružen/a: 29. 01. 2005. (17:27:47)
Postovi: (4C)16
Spol: 
|
|
| [Vrh] |
|
Greda
Forumaš(ica)
Pridružen/a: 01. 07. 2006. (14:00:26)
Postovi: (44)16
Spol: 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 20:13 pet, 24. 11. 2006 Naslov: Postano: 20:13 pet, 24. 11. 2006 Naslov: |
    |
|
|
[quote="C"]Funkcija je f je očito neprekidna na cijeloj domeni. [0,1] je zatvoren skup. Praslika zatvorenog skupa po neprekidnoj funkciji je zatvoren skup (karakterizacija neprekidnosti, na vježbama smo dokazali istu stvar za otvorene skupove). Kako je domena od f zatvorena kugla oko 0 radijusa 1 (ograničen skup), jasno je da će i praslika bilo kojeg skupa po toj funkciji biti ograničen skup.
Dakle, tražena praslika je zatvorena i ograničena što je ekvivalentno s kompaktna.
HTH 8)[/quote]
Neka je [latex]f:A \to {\bf R}^{\bf 2} ,A \subseteq {\bf R}^{\bf 3} ,A = \left\{ {\left( {x,y,z} \right):x^2 + y^2 + z^2 < 1} \right\}[/latex], [latex]f\left( {x,y,z} \right) = \left( {0,0} \right)[/latex]. [latex]f[/latex] je očito neprekidna i [latex]\left\{ {\left( {0,0} \right)} \right\}[/latex] je očito zatvoren u [latex]{\bf R}^{\bf 2}[/latex], ali [latex]f^{ - 1} \left\{ {\left( {0,0} \right)} \right\}[/latex] nije zatvoren. Mislim da se radi o tome da neprekidna funkcija zatvoren skup preslika u zatvoren skup, i to se dosta lako pokaže preko nizova.
| C (napisa): | Funkcija je f je očito neprekidna na cijeloj domeni. [0,1] je zatvoren skup. Praslika zatvorenog skupa po neprekidnoj funkciji je zatvoren skup (karakterizacija neprekidnosti, na vježbama smo dokazali istu stvar za otvorene skupove). Kako je domena od f zatvorena kugla oko 0 radijusa 1 (ograničen skup), jasno je da će i praslika bilo kojeg skupa po toj funkciji biti ograničen skup.
Dakle, tražena praslika je zatvorena i ograničena što je ekvivalentno s kompaktna.
HTH  |
Neka je 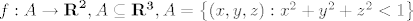 , , 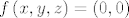 . .  je očito neprekidna i je očito neprekidna i 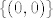 je očito zatvoren u je očito zatvoren u 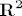 , ali , ali 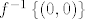 nije zatvoren. Mislim da se radi o tome da neprekidna funkcija zatvoren skup preslika u zatvoren skup, i to se dosta lako pokaže preko nizova. nije zatvoren. Mislim da se radi o tome da neprekidna funkcija zatvoren skup preslika u zatvoren skup, i to se dosta lako pokaže preko nizova.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
vanish
Forumaš(ica)


Pridružen/a: 02. 10. 2005. (22:45:35)
Postovi: (6D)16
Spol: 
Lokacija: stambena zgrada
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
C
Forumaš(ica)

Pridružen/a: 29. 01. 2005. (17:27:47)
Postovi: (4C)16
Spol: 
|
 Postano: 14:41 sub, 25. 11. 2006 Naslov: Postano: 14:41 sub, 25. 11. 2006 Naslov: |
    |
|
|
[quote="vanish"]Ccc, Alene, radi se o tome da je praslika zatvorena u A, a A je zatvoren sam u sebi (osim što je i otvoren).
Bar ja tako mislim. Hm.[/quote]
[quote="nana"]
[quote="C"]unkcija je f je očito neprekidna na cijeloj domeni. [0,1] je zatvoren skup. Praslika zatvorenog skupa po neprekidnoj funkciji je zatvoren [color=red]pod[/color]skup [color=red]od Kugle, tj domene[/color].[/quote]
Mislim da je alen htio nadopisat crveno 8)[/quote]
:ok:
Da, u Alenovom primjeru domena funkcije je skup A (ne R^3), koji je i otvoren i zatvoren u metričkom prostoru A.
Inače, dokaz tvrdnje (praslika zatvorenog skupa po neprekidnoj funkciji je zatvoren skup) se može naći u skripti prof. Ungara, "Matematička analiza 3", Teorem 2.1
Mislim da to ne vrijedi za slike - npr. funkcija arctg:R->R preslikava R (zatvoren skup u domeni) u interval (otvoren skup u kodomeni).
| vanish (napisa): | Ccc, Alene, radi se o tome da je praslika zatvorena u A, a A je zatvoren sam u sebi (osim što je i otvoren).
Bar ja tako mislim. Hm. |
| nana (napisa): |
| C (napisa): | | unkcija je f je očito neprekidna na cijeloj domeni. [0,1] je zatvoren skup. Praslika zatvorenog skupa po neprekidnoj funkciji je zatvoren podskup od Kugle, tj domene. |
Mislim da je alen htio nadopisat crveno  |

Da, u Alenovom primjeru domena funkcije je skup A (ne R^3), koji je i otvoren i zatvoren u metričkom prostoru A.
Inače, dokaz tvrdnje (praslika zatvorenog skupa po neprekidnoj funkciji je zatvoren skup) se može naći u skripti prof. Ungara, "Matematička analiza 3", Teorem 2.1
Mislim da to ne vrijedi za slike - npr. funkcija arctg:R→R preslikava R (zatvoren skup u domeni) u interval (otvoren skup u kodomeni).
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
 Postano: 14:58 ned, 26. 11. 2006 Naslov: Postano: 14:58 ned, 26. 11. 2006 Naslov: |
    |
|
|
[quote="Anonymous"]može pomoć oko 2.b) i 3.a) zadatka.pliz pliz pliz.hvala hvala hvala[/quote]
2b
dokažite da je skup otvoren:
(1) f(x,y)=2x-y nepr na R2-->R
R\{0} otvoren podskup od R (jer je {0} zatvoren)
f^-1 (R\{0}) otvoren podskup od R2
R\{0}={(x,y)e R2 : 2x-y != o}
(2) g(x,y)=x2 + 2y2 nepr na R2-->R
<1, +beskon> podskup R otvoren
g^-1 (<1, +beskon>) otvoren podskup od R2
S=f^-1 (R\{0}) PRESJEK g^-1 (<1, +beskon>) otvoren kao presjek 2 otvorena skupa
| Anonymous (napisa): | | može pomoć oko 2.b) i 3.a) zadatka.pliz pliz pliz.hvala hvala hvala |
2b
dokažite da je skup otvoren:
(1) f(x,y)=2x-y nepr na R2→R
R\{0} otvoren podskup od R (jer je {0} zatvoren)
f^-1 (R\{0}) otvoren podskup od R2
R\{0}={(x,y)e R2 : 2x-y != o}
(2) g(x,y)=x2 + 2y2 nepr na R2→R
<1, +beskon> podskup R otvoren
g^-1 (<1, +beskon>) otvoren podskup od R2
S=f^-1 (R\{0}) PRESJEK g^-1 (<1, +beskon>) otvoren kao presjek 2 otvorena skupa
_________________
I aim to misbehave
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 15:01 ned, 26. 11. 2006 Naslov: Postano: 15:01 ned, 26. 11. 2006 Naslov: |
    |
|
|
[quote="C"][quote="vanish"]Ccc, Alene, radi se o tome da je praslika zatvorena u A, a A je zatvoren sam u sebi (osim što je i otvoren).
Bar ja tako mislim. Hm.[/quote]
[quote="nana"]
[quote="C"]unkcija je f je očito neprekidna na cijeloj domeni. [0,1] je zatvoren skup. Praslika zatvorenog skupa po neprekidnoj funkciji je zatvoren [color=red]pod[/color]skup [color=red]od Kugle, tj domene[/color].[/quote]
Mislim da je alen htio nadopisat crveno 8)[/quote]
:ok:
Da, u Alenovom primjeru domena funkcije je skup A (ne R^3), koji je i otvoren i zatvoren u metričkom prostoru A.
Inače, dokaz tvrdnje (praslika zatvorenog skupa po neprekidnoj funkciji je zatvoren skup) se može naći u skripti prof. Ungara, "Matematička analiza 3", Teorem 2.1
Mislim da to ne vrijedi za slike - npr. funkcija arctg:R->R preslikava R (zatvoren skup u domeni) u interval (otvoren skup u kodomeni).[/quote]
[latex]{\bf R}[/latex] je također i otvoren. Dobro, nije mi baš neki argument, ali ovo bi moglo poslužit: dokaz da je slika zatvorenog skupa zatvoren skup po neprekidnoj funkciji bi išao nekako ovako:
Neka je [latex]f:A \to {\bf R}^k ;A \subseteq {\bf R}^n[/latex], [latex]A[/latex] zatvoren, [latex]f[/latex] neprekidna na [latex]A[/latex]. Kako je [latex]A[/latex] zatvoren, svaki konvergentan niz [latex]\left( {x_n } \right)_n \subseteq A[/latex] ima limes [latex]x_0 \in A[/latex]. Kako je [latex]f[/latex] neprekidna na [latex]A[/latex], vrijedi da je [latex]\mathop {\lim }\limits_{n \to \infty } f\left( {x_n } \right) = f\left( {\mathop {\lim }\limits_{n \to \infty } x_n } \right) = f\left( {x_0 } \right)[/latex], odnosno da svaki konvergentan niz [latex]\left( {y_n } \right)_n \subseteq f\left( A \right)[/latex] ima limes [latex]y_0 \in f\left( A \right)[/latex], odnosno [latex]f\left( A \right)[/latex] je zatvoren.
Sad uzmem "konvergentan" niz koji divergira prema [latex] \pm \infty[/latex], a kako je [latex]{\bf R}[/latex] zatvoren, imam [latex] \pm \infty \in {\bf R}[/latex] i stavim da je [latex]f\left( { - \infty } \right) = - \frac{\pi }{2},f\left( { + \infty } \right) = \frac{\pi }{2}[/latex]. Ovo čak i meni zvuči dosta nategnuto, valjda će netko od asistenata priskočit u pomoć.
Nadam se da je Ungar mislio na topološke prostore, jer u metričkom [latex]{\bf R}^n[/latex] očito ne vrijedi.
Postupak rješavanja za 2.a je sljedeći:
Domena funkcije [latex]f[/latex] je ograničena pa je praslika svakog skupa iz kodomene te funkcije ograničena. [latex]f[/latex] je neprekidna pa je svaka praslika zatvorenog skupa u kodomeni zatvoren skup u [latex]\overline {K\left( {0,1} \right)}[/latex], što znači da postoji [latex]X \subseteq {\bf R}^{\bf 2}[/latex] takav da je [latex]X \cap \overline {K\left( {0,1} \right)} = f^{ - 1} \left( {\left[ {0,1} \right]} \right)[/latex], a kako su oba skupa na lijevoj strani jednakosti zatvorena, slijedi da je i njihov presjek zatvoren, odnosno [latex]f^{ - 1} \left( {\left[ {0,1} \right]} \right)[/latex] je zatvoren. Odavde slijedi kompaktnost.
Evo, još jednom ću napisat jer mislim da to treba snažno naglasit:
Neka je [latex]f:A \to {\bf R}^k ;A \subseteq {\bf R}^n[/latex] i [latex]B \subseteq f\left( A \right)[/latex] zatvoren u [latex]{\bf R}^k[/latex]. Tada je [latex]f^{ - 1} \left( B \right)[/latex] skup koji je zatvoren u [latex]A[/latex]. [b] Ne mora biti zatvoren[/b], ali mora biti zatvoren u [latex]A[/latex].
| C (napisa): | | vanish (napisa): | Ccc, Alene, radi se o tome da je praslika zatvorena u A, a A je zatvoren sam u sebi (osim što je i otvoren).
Bar ja tako mislim. Hm. |
| nana (napisa): |
| C (napisa): | | unkcija je f je očito neprekidna na cijeloj domeni. [0,1] je zatvoren skup. Praslika zatvorenog skupa po neprekidnoj funkciji je zatvoren podskup od Kugle, tj domene. |
Mislim da je alen htio nadopisat crveno  |

Da, u Alenovom primjeru domena funkcije je skup A (ne R^3), koji je i otvoren i zatvoren u metričkom prostoru A.
Inače, dokaz tvrdnje (praslika zatvorenog skupa po neprekidnoj funkciji je zatvoren skup) se može naći u skripti prof. Ungara, "Matematička analiza 3", Teorem 2.1
Mislim da to ne vrijedi za slike - npr. funkcija arctg:R→R preslikava R (zatvoren skup u domeni) u interval (otvoren skup u kodomeni). |
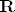 je također i otvoren. Dobro, nije mi baš neki argument, ali ovo bi moglo poslužit: dokaz da je slika zatvorenog skupa zatvoren skup po neprekidnoj funkciji bi išao nekako ovako: je također i otvoren. Dobro, nije mi baš neki argument, ali ovo bi moglo poslužit: dokaz da je slika zatvorenog skupa zatvoren skup po neprekidnoj funkciji bi išao nekako ovako:
Neka je 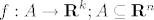 , ,  zatvoren, zatvoren,  neprekidna na neprekidna na  . Kako je . Kako je  zatvoren, svaki konvergentan niz zatvoren, svaki konvergentan niz 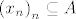 ima limes ima limes 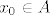 . Kako je . Kako je  neprekidna na neprekidna na  , vrijedi da je , vrijedi da je 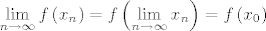 , odnosno da svaki konvergentan niz , odnosno da svaki konvergentan niz 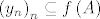 ima limes ima limes 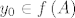 , odnosno , odnosno 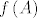 je zatvoren. je zatvoren.
Sad uzmem "konvergentan" niz koji divergira prema  , a kako je , a kako je 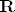 zatvoren, imam zatvoren, imam 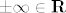 i stavim da je i stavim da je 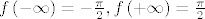 . Ovo čak i meni zvuči dosta nategnuto, valjda će netko od asistenata priskočit u pomoć. . Ovo čak i meni zvuči dosta nategnuto, valjda će netko od asistenata priskočit u pomoć.
Nadam se da je Ungar mislio na topološke prostore, jer u metričkom 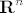 očito ne vrijedi. očito ne vrijedi.
Postupak rješavanja za 2.a je sljedeći:
Domena funkcije  je ograničena pa je praslika svakog skupa iz kodomene te funkcije ograničena. je ograničena pa je praslika svakog skupa iz kodomene te funkcije ograničena.  je neprekidna pa je svaka praslika zatvorenog skupa u kodomeni zatvoren skup u je neprekidna pa je svaka praslika zatvorenog skupa u kodomeni zatvoren skup u 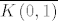 , što znači da postoji , što znači da postoji 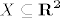 takav da je takav da je 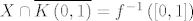 , a kako su oba skupa na lijevoj strani jednakosti zatvorena, slijedi da je i njihov presjek zatvoren, odnosno , a kako su oba skupa na lijevoj strani jednakosti zatvorena, slijedi da je i njihov presjek zatvoren, odnosno 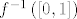 je zatvoren. Odavde slijedi kompaktnost. je zatvoren. Odavde slijedi kompaktnost.
Evo, još jednom ću napisat jer mislim da to treba snažno naglasit:
Neka je 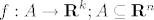 i i 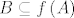 zatvoren u zatvoren u 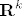 . Tada je . Tada je 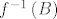 skup koji je zatvoren u skup koji je zatvoren u  . Ne mora biti zatvoren, ali mora biti zatvoren u . Ne mora biti zatvoren, ali mora biti zatvoren u  . .
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
Zadnja promjena: alen; 15:51 ned, 26. 11. 2006; ukupno mijenjano 8 put/a.
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
Debla
Forumaš(ica)

Pridružen/a: 06. 12. 2005. (16:54:24)
Postovi: (94)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vini
Forumaš(ica)


Pridružen/a: 01. 09. 2006. (18:10:50)
Postovi: (9E)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
 Postano: 18:22 ned, 26. 11. 2006 Naslov: Postano: 18:22 ned, 26. 11. 2006 Naslov: |
    |
|
|
[quote="Debla"]jel neko rješio 3.c s probnog kolokvija..
[/quote]
{ (x,y,z) e [0,1]*[0,1]*[0,1] : (x^2 +2y, x-y-z) = (1,1) } (kompaktnost?)
skup je ogranicen jer je sadrzan u [0,1]^3 koji je i sam ogranicen..
skup je zatvoren: f: R^3 -> R^2.. f(x,y,z) = ( x^2 + 2y, x- y -z ) neprekidna
nas skup je f^(-1) ({1,1)} => zatvorena
(tocka zatvorena)
prsjek toga i [0,1] je zatvorena..
| Debla (napisa): | jel neko rješio 3.c s probnog kolokvija..
|
{ (x,y,z) e [0,1]*[0,1]*[0,1] : (x^2 +2y, x-y-z) = (1,1) } (kompaktnost?)
skup je ogranicen jer je sadrzan u [0,1]^3 koji je i sam ogranicen..
skup je zatvoren: f: R^3 → R^2.. f(x,y,z) = ( x^2 + 2y, x- y -z ) neprekidna
nas skup je f^(-1) ({1,1)} ⇒ zatvorena
(tocka zatvorena)
prsjek toga i [0,1] je zatvorena..
_________________
I aim to misbehave
|
|
| [Vrh] |
|
Debla
Forumaš(ica)

Pridružen/a: 06. 12. 2005. (16:54:24)
Postovi: (94)16
Spol: 
|
|
| [Vrh] |
|
vini
Forumaš(ica)


Pridružen/a: 01. 09. 2006. (18:10:50)
Postovi: (9E)16
Spol: 
|
|
| [Vrh] |
|
Bee
Forumaš(ica)
Pridružen/a: 31. 01. 2005. (11:27:34)
Postovi: (91)16
Spol: 
Lokacija: Hicksville
|
|
| [Vrh] |
|
|


















