| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
grizko
Forumaš(ica)

Pridružen/a: 19. 02. 2004. (23:21:26)
Postovi: (6)16
|
|
| [Vrh] |
|
Gost
|
 Postano: 22:36 čet, 6. 9. 2007 Naslov: Postano: 22:36 čet, 6. 9. 2007 Naslov: |
    |
|
|
Napisi jedn. tangente kroz (b, f(b)). Da bi Newtonova m. ciklirala, tangenta mora prolaziti kroz (-b, 0), to uvrsti. Tu f-ju interpoliraj metodom bisekcije na danom intervalu.
Vec je bilo rijeci o trazenju tocke cikliranja, pogledaj prethodne postove.
Pozdrav
Napisi jedn. tangente kroz (b, f(b)). Da bi Newtonova m. ciklirala, tangenta mora prolaziti kroz (-b, 0), to uvrsti. Tu f-ju interpoliraj metodom bisekcije na danom intervalu.
Vec je bilo rijeci o trazenju tocke cikliranja, pogledaj prethodne postove.
Pozdrav
|
|
| [Vrh] |
|
Ziggy
Forumaš(ica)

Pridružen/a: 29. 04. 2007. (01:01:22)
Postovi: (28)16
Spol: 
|
|
| [Vrh] |
|
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
jana
Forumaš(ica)
Pridružen/a: 16. 07. 2004. (00:15:21)
Postovi: (8)16
|
 Postano: 18:33 pet, 14. 9. 2007 Naslov: Postano: 18:33 pet, 14. 9. 2007 Naslov: |
    |
|
|
ispitivao je, zapravo, pisali smo. nije bilo tesko. svi su prosli. zapravo, svi su digli po jednu ocjenu.
pitanja:
1. eulerova metoda
2. iterativne metode za racunanje Ax=b (jacobijeva i krilovljevi potprostori)
3. SVD dekompozicija
bilo je i 4. dodatno pitanje. ako koje od gornjih ne znas, mozes napisat i sta znas o QR faktorizaciji i kako to rjesava problem minimizacije...
kad rijesis sve, odes do profesora i malo te propita ako nesto nisi bas dobro napisao
sretno
ispitivao je, zapravo, pisali smo. nije bilo tesko. svi su prosli. zapravo, svi su digli po jednu ocjenu.
pitanja:
1. eulerova metoda
2. iterativne metode za racunanje Ax=b (jacobijeva i krilovljevi potprostori)
3. SVD dekompozicija
bilo je i 4. dodatno pitanje. ako koje od gornjih ne znas, mozes napisat i sta znas o QR faktorizaciji i kako to rjesava problem minimizacije...
kad rijesis sve, odes do profesora i malo te propita ako nesto nisi bas dobro napisao
sretno
|
|
| [Vrh] |
|
fugy
Gost
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 9:40 ned, 16. 9. 2007 Naslov: Postano: 9:40 ned, 16. 9. 2007 Naslov: |
    |
|
|
fugy ,
na math.hr/~hyde imate pismeni ispit sa nedavnog roka, te link na jos nekoliko njih. Ukoliko ste rijesili barem jedan rok, to ce vam biti vise nego dovoljno da dobijete ocjenu odlican. Pitanja su standardna i nema vecih odstupanja u rokovima. Ostaviti cu pismeni ispit sa zadnje roka u skriptarnici, no mislim da vam on, za efikasno ucenje (i polaganje) ispita nece biti potreban.
fugy ,
na math.hr/~hyde imate pismeni ispit sa nedavnog roka, te link na jos nekoliko njih. Ukoliko ste rijesili barem jedan rok, to ce vam biti vise nego dovoljno da dobijete ocjenu odlican. Pitanja su standardna i nema vecih odstupanja u rokovima. Ostaviti cu pismeni ispit sa zadnje roka u skriptarnici, no mislim da vam on, za efikasno ucenje (i polaganje) ispita nece biti potreban.
|
|
| [Vrh] |
|
fugolina
Forumaš(ica)

Pridružen/a: 01. 09. 2004. (18:14:29)
Postovi: (68)16
Lokacija: zagreb
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 13:48 pet, 21. 9. 2007 Naslov: Postano: 13:48 pet, 21. 9. 2007 Naslov: |
    |
|
|
rok 05.09.
1Fiju [latex]f(x)=\sqrt{3x+5}[/latex] aproksimirajte Newtonovim int. polin. st 3 na Čebiševljevoj mreži intervala [-1.5,1.5].
Pogledajte na wikipediji o [url=http://en.wikipedia.org/wiki/Chebyshev_nodes] Čebiševljevim čvorovima[/url] i o [url=http://en.wikipedia.org/wiki/Newton_polynomials]Newtonovim polinomima[/url], i rijesili ste zadatak.
2. Metodom bisekcije pronadite tocku cikliranja Newtonove metode za nalaženje nultocke fije [latex]f(x)=arcctg{x}-\frac{\pi}{2}[/latex] na intervalu [-0.15,0.1]. td greska bude manja od [latex]10^{-2}[/latex]. Unaprijed izracunajte broj iteracija potrebnih za dostizanja trazene nejednakosti.
Sada na wikipediji pogledajte o [url=http://en.wikipedia.org/wiki/Newton_method]Newtonovoj metodi[/url] i o [url=http://en.wikipedia.org/wiki/Bisection_method] metodi bisekcije[/url] i rijesili ste zadatak. Ili uocite da je [latex]arcctg{x}-\frac{\pi}{2}=-\arctan{x}[/latex], a takav smo zadatak radili na vjezbama. O tockama cikliranja Newtonove metode vam pise na ovom topicu.
3.Rijesite odj [latex]y'(x)=\frac{x^2+2\cdot y(x)}{x},y(1)=0[/latex] pomocu Eulerove metode na intervalu [1,4] i na mrezi od n=6 jednakih dijelova
Sada ponovno na wikipediu pogledati o [url=http://en.wikipedia.org/wiki/Euler_method]Eulerovoj metodi[/url] , te je [latex]h=\frac{b-a}{n}[/latex].
4.Ekspl. metodom konacnih diferencija rijestie rubni problem :
[latex]\frac{\partial u}{\partial \tau}=\frac{\parital ^2 u}{\partial x^2},x\in <-1.6,1.6>,\tau \in <0,0.9>[/latex],
[latex]u(-1.6,\tau)=\cos{\tau}, u(1.6,\tau)=\sqrt{\tau +3}, u(x,0)=x[/latex], na mrezi zadanoj sa (a)[latex]h_x=0.6,h_\tau=0.5[/latex] (b)[latex]h_x=0.8,h_\tau=0.3[/latex]
Pogledati o [url=http://en.wikipedia.org/wiki/Finite_difference_method]metodi konacnih diferencija[/url], pogledajte nesta u uvjetu stabilnosti za eks. metodu i rijesite samo (b).
5.Pretpostavimo da zelimo rijesiti lin. problem najmanjih kvadrata [latex]\min_x ||Ax-b||_2,A\in\mathbb{R}^{m\times n},b\in\mathbb{R}^m,x\in\mathbb{R}^n,m\geq n[/latex], te objasniti okako rijesiti problem preko QR faktorizacije.
Ovdje bi kao nesta trebali napisati no pogledajte o [url=http://en.wikipedia.org/wiki/QR_decomposition]QR dekompoziciji[/url] i o [url=http://en.wikipedia.org/wiki/Linear_least_squares]problemu najmanjih kvadrata[/url].
Dakle, [latex]||Ax-b||_2=||Q{R \choose 0}x-b||_2=||{R \choose 0}x-c||_2[/latex] , gdje [latex]c=Q^{\tau}b={c_1 \choose c_2}[/latex] pa imamo [latex]||{ Rx-c_1 \choose -c_2}||_2=\sqrt{||Rx-c_1||_2+||c_2||_2}[/latex] , te buduci da samo prvi clan ovisi o x, samo kod njega provodimo minimizaciju.
Sve je vrlo jednostavno, cak niste trebali niti biti na vjezbama (sto ne preporucujem), nego se samo morate znati koristiti internetom, tj. wikipedijom.
rok 05.09.
1Fiju 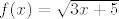 aproksimirajte Newtonovim int. polin. st 3 na Čebiševljevoj mreži intervala [-1.5,1.5]. aproksimirajte Newtonovim int. polin. st 3 na Čebiševljevoj mreži intervala [-1.5,1.5].
Pogledajte na wikipediji o Čebiševljevim čvorovima i o Newtonovim polinomima, i rijesili ste zadatak.
2. Metodom bisekcije pronadite tocku cikliranja Newtonove metode za nalaženje nultocke fije 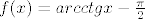 na intervalu [-0.15,0.1]. td greska bude manja od na intervalu [-0.15,0.1]. td greska bude manja od 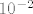 . Unaprijed izracunajte broj iteracija potrebnih za dostizanja trazene nejednakosti. . Unaprijed izracunajte broj iteracija potrebnih za dostizanja trazene nejednakosti.
Sada na wikipediji pogledajte o Newtonovoj metodi i o metodi bisekcije i rijesili ste zadatak. Ili uocite da je 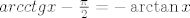 , a takav smo zadatak radili na vjezbama. O tockama cikliranja Newtonove metode vam pise na ovom topicu. , a takav smo zadatak radili na vjezbama. O tockama cikliranja Newtonove metode vam pise na ovom topicu.
3.Rijesite odj 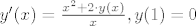 pomocu Eulerove metode na intervalu [1,4] i na mrezi od n=6 jednakih dijelova pomocu Eulerove metode na intervalu [1,4] i na mrezi od n=6 jednakih dijelova
Sada ponovno na wikipediu pogledati o Eulerovoj metodi , te je 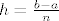 . .
4.Ekspl. metodom konacnih diferencija rijestie rubni problem :
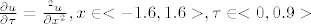 , ,
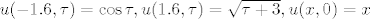 , na mrezi zadanoj sa (a) , na mrezi zadanoj sa (a)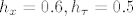 (b) (b)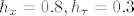
Pogledati o metodi konacnih diferencija, pogledajte nesta u uvjetu stabilnosti za eks. metodu i rijesite samo (b).
5.Pretpostavimo da zelimo rijesiti lin. problem najmanjih kvadrata 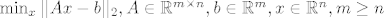 , te objasniti okako rijesiti problem preko QR faktorizacije. , te objasniti okako rijesiti problem preko QR faktorizacije.
Ovdje bi kao nesta trebali napisati no pogledajte o QR dekompoziciji i o problemu najmanjih kvadrata.
Dakle, 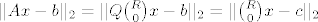 , gdje , gdje 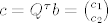 pa imamo pa imamo 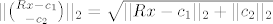 , te buduci da samo prvi clan ovisi o x, samo kod njega provodimo minimizaciju. , te buduci da samo prvi clan ovisi o x, samo kod njega provodimo minimizaciju.
Sve je vrlo jednostavno, cak niste trebali niti biti na vjezbama (sto ne preporucujem), nego se samo morate znati koristiti internetom, tj. wikipedijom.
Zadnja promjena: Mr.Doe; 15:18 sub, 22. 9. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
|




