| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
zzsan
Forumaš(ica)

Pridružen/a: 25. 11. 2005. (20:53:14)
Postovi: (89)16
|
|
| [Vrh] |
|
beba
Forumaš(ica)


Pridružen/a: 17. 08. 2006. (00:00:41)
Postovi: (41)16
Lokacija: st-ZG
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
 Postano: 16:17 uto, 11. 11. 2008 Naslov: Postano: 16:17 uto, 11. 11. 2008 Naslov: |
    |
|
|
[quote="teja"]da li bi mi netko mogao riješiti zad 2.12? integral me muči... barem neku ideju kako ga rješit... [size=7]čovjek bi pomislio da ćeš nakon 3 god znat rješit integral, al ne....:([/size][/quote]
Bi! :D
[latex] f(x)=\frac{1}{b-a} , x\in [a,b][/latex] , 0 inače.
Znamo da je funkcija distribucije [latex] F(x)=\int_{-\infty}^{x} f(t) dt [/latex]
Sada imamo tri slučaja:
[latex] x<a, F(x)=\int_{-\infty}^{x} \frac{1}{b-a} dt[/latex]
Pošto nam je f(x)=0 na [latex] [-\infty,a> \Rightarrow F(x)=0[/latex]
[latex] a\leq x\leq b, F(X)=\int_{-\infty}^{x} \frac{1}{b-a} dt=\frac{1}{b-a} t|_{a}^{x} [/latex] jer je na ostatku [latex] [-\infty,a> f(x)=0 [/latex]
Pa je to [latex] \frac{1}{b-a} (x-a)=\frac{x-a}{b-a} [/latex]
I konačno [latex] x>b [/latex]
[latex] F(x)=\int_{-\infty}^{x} \frac{1}{b-a}dt [/latex], sada pošto je x>b i [latex] f(x)=0, x\notin [a,b] [/latex] od integrala nam ostaje samo :
[latex] \int_{a}^{b} \frac{1}{b-a}dt=\frac{b-a}{b-a}=1 [/latex]
Sad drugi dio možeš sama :)
| teja (napisa): | da li bi mi netko mogao riješiti zad 2.12? integral me muči... barem neku ideju kako ga rješit... čovjek bi pomislio da ćeš nakon 3 god znat rješit integral, al ne.... |
Bi! 
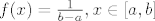 , 0 inače. , 0 inače.
Znamo da je funkcija distribucije 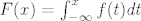
Sada imamo tri slučaja:
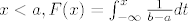
Pošto nam je f(x)=0 na 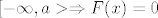
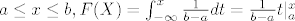 jer je na ostatku jer je na ostatku 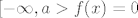
Pa je to 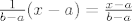
I konačno 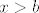
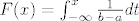 , sada pošto je x>b i , sada pošto je x>b i 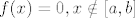 od integrala nam ostaje samo : od integrala nam ostaje samo :
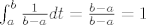
Sad drugi dio možeš sama 
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
 Postano: 22:58 uto, 11. 11. 2008 Naslov: Postano: 22:58 uto, 11. 11. 2008 Naslov: |
    |
|
|
[quote="teja"]joj...fala ti na trudu, ali to je 2.11.
pitala san za 2.12....ovo s trećim i četvrtim momentom....:)[/quote]
No problem, sam na stranici od statistike među zadacima je to 2.13, but then again u mojim papirima (prastarim) je to cjelo poglavlje 1. :lol:
Znači:
[latex]\displaystyle \mathbb{E}[X^3] =\int_{-\infty}^{+\infty} x^3\frac{1}{\sigma\sqrt{2\pi}}e^{\frac{-(x-\mu)^2}{2\sigma^2}}dx= \frac{1}{\sigma\sqrt{2\pi}} \int_{-\infty}^{+\infty} x^3e^{\frac{-(x-\mu)^2}{2\sigma^2}}dx [/latex]
Supstitucija:
[latex]\displaystyle t=\frac{x-\mu}{\sigma}, dt=\frac{dx}{\sigma}[/latex], pa imamo
[latex] \displaystyle \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty} (t\sigma+\mu)^3e^{\frac{-t^2}{2}}dt=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}( (t\sigma)^3+3t\sigma\mu^2+3(t\sigma)^2\mu + \mu^3)e^{\frac{-t^2}{2}}dt=\frac{\sigma^3}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}t^3e^{\frac{-t^2}{2}}dt +\frac{3\sigma\mu^2}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}te^{\frac{-t^2}{2}}dt+\frac{3\sigma^2\mu}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}t^2e^{\frac{-t^2}{2}}dt+\frac{\mu^3}{\sqrt{2\pi}}\int_{-\infty}^{+\infty} e^{\frac{-t^2}{2}}dt [/latex]
E sad, prva dva integrala su 0 jer su to neparne funkcije na simetričnoj domeni (da sam se bar tog sjetio na numeričkoj :lol:)
Ostaju nam samo dva:
[latex] \displaystyle \int t^2e^{\frac{-t^2}{2}}dt=\left{t=u, du=1, v'=te^{\frac{-t^2}{2}}, v=-e^{\frac{-t^2}{2}} \riht}=-te^{\frac{-t^2}{2}}+\int e^{\frac{-t^2}{2}}dt [/latex]
I sada:
[latex] \displaystyle
\frac{3\sigma^2\mu}{\sqrt{2\pi}}[-te^{\frac{-t^2}{2}}|_{-\infty}^{+\infty} + \int_{-\infty}^{+\infty} e^{\frac{-t^2}{2}}dt]+ \frac{\mu^3}{\sqrt{2\pi}}\int_{-\infty}^{+\infty} e^{\frac{-t^2}{2}}dt=3\sigma^2\mu+\mu^3 [/latex]
A za četvrti ide isto tako, neda mi se više pisat... pozz :D
| teja (napisa): | joj...fala ti na trudu, ali to je 2.11.
pitala san za 2.12....ovo s trećim i četvrtim momentom.... |
No problem, sam na stranici od statistike među zadacima je to 2.13, but then again u mojim papirima (prastarim) je to cjelo poglavlje 1. 
Znači:
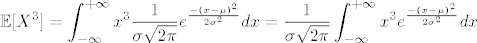
Supstitucija:
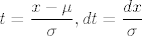 , pa imamo , pa imamo
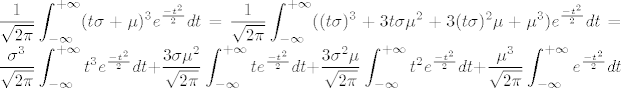
E sad, prva dva integrala su 0 jer su to neparne funkcije na simetričnoj domeni (da sam se bar tog sjetio na numeričkoj  ) )
Ostaju nam samo dva:
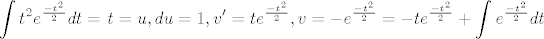
I sada:
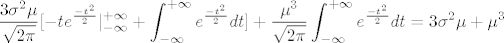
A za četvrti ide isto tako, neda mi se više pisat... pozz 
|
|
| [Vrh] |
|
teja not logged?
Gost
|
|
| [Vrh] |
|
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
andreao
Forumaš(ica)


Pridružen/a: 10. 02. 2005. (12:08:18)
Postovi: (46F)16
Lokacija: SK
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
andreao
Forumaš(ica)


Pridružen/a: 10. 02. 2005. (12:08:18)
Postovi: (46F)16
Lokacija: SK
|
|
| [Vrh] |
|
5ra
Forumaš(ica)


Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
 Postano: 0:51 ned, 16. 11. 2008 Naslov: Postano: 0:51 ned, 16. 11. 2008 Naslov: |
    |
|
|
što se tiče zadatka 1.19:
vrijeme je neprekidno statističko obilježje, prema tome podaci se dijele u razrede. histogram je krivo nacrtan u rješenju.
kad uzmemo k=6 ispadne c=1 što je granični slučaj pa se razredi uzimaju ovako:
[4, 5]
<5, 6]
<6, 7]
...
<9, 10]
to inače baš i nije dobro jer bi granice razreda trebale imati jednu decimalu više od podataka, ali u ovom slučaj zbog toga što imamo 6 razreda sa razmakom 1, a podaci idu od 4 do 10 to se ne može. asistentica ninčević rekla je da se onda to najčešće radi ovako, može se i uzeti da je diskretni skup, ali ovo je bolje rješenje.
nisam probala ali vjerojatno bi bilo okej da uzmemo k=5 ili k=7, ko voli nek proba :))
što se tiče zadatka 1.19:
vrijeme je neprekidno statističko obilježje, prema tome podaci se dijele u razrede. histogram je krivo nacrtan u rješenju.
kad uzmemo k=6 ispadne c=1 što je granični slučaj pa se razredi uzimaju ovako:
[4, 5]
<5, 6]
<6, 7]
...
<9, 10]
to inače baš i nije dobro jer bi granice razreda trebale imati jednu decimalu više od podataka, ali u ovom slučaj zbog toga što imamo 6 razreda sa razmakom 1, a podaci idu od 4 do 10 to se ne može. asistentica ninčević rekla je da se onda to najčešće radi ovako, može se i uzeti da je diskretni skup, ali ovo je bolje rješenje.
nisam probala ali vjerojatno bi bilo okej da uzmemo k=5 ili k=7, ko voli nek proba  ) )
|
|
| [Vrh] |
|
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
 Postano: 0:58 ned, 16. 11. 2008 Naslov: Postano: 0:58 ned, 16. 11. 2008 Naslov: |
    |
|
|
e super... znači ipak sam bila u pravu što se razreda tiče , više nisam znala kud bih sa sobom...
e baš to, dobila sam c=1 i onda su me te granice mučile...
jer sam stavljala npr [4, 5> i nikak dobiti ko u rješenju :roll:
luda sam bila...
pa pomaknem na c=1.1 pa dobim ok frekvencije, ali mi onda r[size=9]i[/size] ne paše ko na grafu tj izgledalo mi ko da stavljaju r[size=8]i[/size] umjesto r/c...
znači cijela kvaka je bila u granicama :shock:
puno ti hvala, već sam mislila da nisam normalna...
e super... znači ipak sam bila u pravu što se razreda tiče , više nisam znala kud bih sa sobom...
e baš to, dobila sam c=1 i onda su me te granice mučile...
jer sam stavljala npr [4, 5> i nikak dobiti ko u rješenju 
luda sam bila...
pa pomaknem na c=1.1 pa dobim ok frekvencije, ali mi onda ri ne paše ko na grafu tj izgledalo mi ko da stavljaju ri umjesto r/c...
znači cijela kvaka je bila u granicama 
puno ti hvala, već sam mislila da nisam normalna...
_________________
potpis
|
|
| [Vrh] |
|
5ra
Forumaš(ica)


Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
|
| [Vrh] |
|
Debla
Forumaš(ica)

Pridružen/a: 06. 12. 2005. (16:54:24)
Postovi: (94)16
Spol: 
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
|



















