| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 18:36 ned, 4. 11. 2007 Naslov: Postano: 18:36 ned, 4. 11. 2007 Naslov: |
    |
|
|
[quote="desire"]4. a) [latex] n! [/latex]
b) [latex] \frac {{n \choose 2}{n-2 \choose 2}{n-4 \choose 2}\cdot\cdot\cdot{2 \choose 2}}{(\frac{n}{2})!} [/latex]
S tim da za ovaj [latex](\frac{n}{2})! [/latex] nisam sigurna jel mi zapravo treba ili ne.
c) 1
d) [latex]{2n-1 \choose n}[/latex][/quote]
s (a) i (c) se slažem. (d) nemam ideju. da li možeš objasniti kako si to dobila?
(b) ti sigurno nije točan, barem ne u potpunosti, jer n može biti neparan. što bi u tom slučaju bilo [latex](\frac{n}{2})! [/latex] ? :roll:
uglavnom, mislim da baš o parnosti od n i ovisi rješenje.
ja mislim da, ako je n neparan, takva funkcija ni ne postoji, jer bi morala postojati barem jedna fiksna točka.
s druge strane, kad je n paran dobivam (n-1)*(n-3)*...3*1. mislim da se to može zapisati i kao [color=red](n-3)!![/color]
zašto tako? pa uzmem jedan element i na n-1 načina odaberem onog u kojeg će se on preslikati i koji će se u njega (jer je funkcija jednaka svom inverzu). sada imam n-2 elementa. opet uzmem jednog i na n-3 načina odaberem njegovu sliku... i tako to ide dok sve ne potrošim.
ti biraš svaki put po dva elementa, što se čini ok, ali to definitivno treba nečime podijeliti, jer ti nije bitan redoslijed odabira. bitno je koji element se preslikava u koji. možda je ovako kako si napisala ok - to ne znam.
a kako (d)?
edit:
[color=red](n-1)!!, a ne (n-3)!!
ne znam šta mi je bilo.[/color]
| desire (napisa): | 4. a) 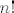
b) 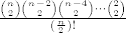
S tim da za ovaj 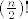 nisam sigurna jel mi zapravo treba ili ne. nisam sigurna jel mi zapravo treba ili ne.
c) 1
d) 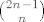 |
s (a) i (c) se slažem. (d) nemam ideju. da li možeš objasniti kako si to dobila?
(b) ti sigurno nije točan, barem ne u potpunosti, jer n može biti neparan. što bi u tom slučaju bilo 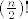 ? ? 
uglavnom, mislim da baš o parnosti od n i ovisi rješenje.
ja mislim da, ako je n neparan, takva funkcija ni ne postoji, jer bi morala postojati barem jedna fiksna točka.
s druge strane, kad je n paran dobivam (n-1)*(n-3)*...3*1. mislim da se to može zapisati i kao (n-3)!!
zašto tako? pa uzmem jedan element i na n-1 načina odaberem onog u kojeg će se on preslikati i koji će se u njega (jer je funkcija jednaka svom inverzu). sada imam n-2 elementa. opet uzmem jednog i na n-3 načina odaberem njegovu sliku... i tako to ide dok sve ne potrošim.
ti biraš svaki put po dva elementa, što se čini ok, ali to definitivno treba nečime podijeliti, jer ti nije bitan redoslijed odabira. bitno je koji element se preslikava u koji. možda je ovako kako si napisala ok - to ne znam.
a kako (d)?
edit:
(n-1)!!, a ne (n-3)!!
ne znam šta mi je bilo.
_________________
ima let u finish
Zadnja promjena: ma; 23:30 ned, 4. 11. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
 Postano: 21:06 ned, 4. 11. 2007 Naslov: Postano: 21:06 ned, 4. 11. 2007 Naslov: |
    |
|
|
U tome i je poanta, da n ne moze biti neparan jer bi onda postojala fiksna tocka. Znaci moze [latex]\frac{n}{2}[/latex]. E sad, jel moj nacin tocan, to ne znam, zato sam i napisla rjesenja, da se javi netko ko mozda razmislja drugacije od mene. ;)
Ja sam uzimala po 2 elementa, znaci element i ono u sto se preslika (npr. f(3)=5 znaci i f(5)=3). Ta 2 izbacim i biram dalje iduca 2. Dijelim sa [latex](\frac{n}{2})![/latex] jer takvih parova ima [latex]\frac{n}{2}[/latex], a poredak nije bitan.
Ponavljam, ne garantitarm tocnost rjesenja, ali ovo je forum, tu smo da raspravimo i skupa dodjemo do nekog zakljucka. :)
U tome i je poanta, da n ne moze biti neparan jer bi onda postojala fiksna tocka. Znaci moze 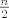 . E sad, jel moj nacin tocan, to ne znam, zato sam i napisla rjesenja, da se javi netko ko mozda razmislja drugacije od mene. . E sad, jel moj nacin tocan, to ne znam, zato sam i napisla rjesenja, da se javi netko ko mozda razmislja drugacije od mene. 
Ja sam uzimala po 2 elementa, znaci element i ono u sto se preslika (npr. f(3)=5 znaci i f(5)=3). Ta 2 izbacim i biram dalje iduca 2. Dijelim sa 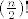 jer takvih parova ima jer takvih parova ima 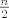 , a poredak nije bitan. , a poredak nije bitan.
Ponavljam, ne garantitarm tocnost rjesenja, ali ovo je forum, tu smo da raspravimo i skupa dodjemo do nekog zakljucka. 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
amorphis
Forumaš(ica)


Pridružen/a: 10. 02. 2007. (23:15:13)
Postovi: (101)16
Lokacija: zg
|
 Postano: 12:35 pon, 5. 11. 2007 Naslov: Postano: 12:35 pon, 5. 11. 2007 Naslov: |
    |
|
|
meni su 1, 2, 4a,c,d, 7 i 8 isti kao i kod desire
mala preporuka; usporedite zadatke iz 3.dz sa zadacima
iz propisane literature (M.Cvitković, Kombinatorika -
8.poglavlje), možda pomogne :)
meni su 1, 2, 4a,c,d, 7 i 8 isti kao i kod desire
mala preporuka; usporedite zadatke iz 3.dz sa zadacima
iz propisane literature (M.Cvitković, Kombinatorika -
8.poglavlje), možda pomogne 
|
|
| [Vrh] |
|
shimija
Forumaš(ica)


Pridružen/a: 22. 01. 2007. (18:33:54)
Postovi: (138)16
Spol: 
Lokacija: Spljit
|
 Postano: 17:42 pon, 5. 11. 2007 Naslov: Postano: 17:42 pon, 5. 11. 2007 Naslov: |
    |
|
|
[quote="ma"][quote="desire"]U tome i je poanta, da n ne moze biti neparan jer bi onda postojala fiksna tocka. Znaci moze [latex]\frac{n}{2}[/latex]. [/quote]
pa znam, ali treba naglasiti u rješenju da n nije neparan :wink:
a kako dobiješ ono pod (d)? :?[/quote]
slika od proizvoljnog elementa iz skupa A može bit bilo koji broj od 1 do n. zato gledamo n-kombinacije s ponavljanjem skupa {1,2...,n} jer ce nam tada ta kombinacija predstavljati skup svih slika,a poredak u njima je na jedinstven način određen pa svaka ta kombinacija predstavlje jednu moguću rastuću funkciju.
kad gledaš stogi rast (c) uzmeš n-kombinaciju bez ponavljanja jer slike nikoja dva ele. ne smiju biti iste a to je u ovom slučaju 1
| ma (napisa): | | desire (napisa): | U tome i je poanta, da n ne moze biti neparan jer bi onda postojala fiksna tocka. Znaci moze 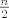 . . |
pa znam, ali treba naglasiti u rješenju da n nije neparan 
a kako dobiješ ono pod (d)?  |
slika od proizvoljnog elementa iz skupa A može bit bilo koji broj od 1 do n. zato gledamo n-kombinacije s ponavljanjem skupa {1,2...,n} jer ce nam tada ta kombinacija predstavljati skup svih slika,a poredak u njima je na jedinstven način određen pa svaka ta kombinacija predstavlje jednu moguću rastuću funkciju.
kad gledaš stogi rast (c) uzmeš n-kombinaciju bez ponavljanja jer slike nikoja dva ele. ne smiju biti iste a to je u ovom slučaju 1
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Miha Keber
Forumaš(ica)

Pridružen/a: 18. 10. 2006. (20:16:56)
Postovi: (26)16
Spol: 
|
|
| [Vrh] |
|
shimija
Forumaš(ica)


Pridružen/a: 22. 01. 2007. (18:33:54)
Postovi: (138)16
Spol: 
Lokacija: Spljit
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
napraviculom
Forumaš(ica)

Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol: 
Lokacija: Scranton
|
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
 Postano: 8:59 uto, 6. 11. 2007 Naslov: Postano: 8:59 uto, 6. 11. 2007 Naslov: |
    |
|
|
[quote="ma"][quote="goc"]ja dobio b) [latex] 2^{\frac{n(n+1)}{2}} [/latex] i
e) [latex] 3^{\frac{n(n-1)}{2}} [/latex][/quote]
(b) nam je isti. @matmih - to ti nisu disjunktni slučajevi.
ali pod (e) mi je [latex] 3^{\frac{n(n-1)}{2}} \cdot 2^n [/latex], zato što mislim da smijemo imati i par (x,x). :?[/quote]
ee, al kolko ja znam(znaci, lako je moguce da sam u krivu, definicije mi nisu jaca strana :D) ako je refleksivna nije da mozemo imati (x,x) nego moramo imati (x,x) pa onda onih 2^n nije potrebno... mislim da sam u pravu ovdje jer inace mi ni c) dio ne valja a za to se niko jos nije bunio...
inace, predobar koncert jucer, bar ono sta sam ja cuo :guitar:
| ma (napisa): | | goc (napisa): | ja dobio b) 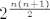 i i
e) 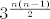 |
(b) nam je isti. @matmih - to ti nisu disjunktni slučajevi.
ali pod (e) mi je 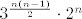 , zato što mislim da smijemo imati i par (x,x). , zato što mislim da smijemo imati i par (x,x).  |
ee, al kolko ja znam(znaci, lako je moguce da sam u krivu, definicije mi nisu jaca strana  ) ako je refleksivna nije da mozemo imati (x,x) nego moramo imati (x,x) pa onda onih 2^n nije potrebno... mislim da sam u pravu ovdje jer inace mi ni c) dio ne valja a za to se niko jos nije bunio... ) ako je refleksivna nije da mozemo imati (x,x) nego moramo imati (x,x) pa onda onih 2^n nije potrebno... mislim da sam u pravu ovdje jer inace mi ni c) dio ne valja a za to se niko jos nije bunio...
inace, predobar koncert jucer, bar ono sta sam ja cuo 
|
|
| [Vrh] |
|
|





















