Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

3. zadatak EM1 dz3 - indukcija (zadatak)
WWW:
Idite na Prethodno  1, 2
Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Elementarna matematika 1 i 2
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
vsego
Site Admin
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: zombi
Sarma = la pohva - posuda
854 = 1068 - 214
Lokacija: /sbin/init
PostPostano: 19:25 sri, 21. 11. 2007    Naslov: Citirajte i odgovorite
[latex]$\begin{align*}
\frac{1}{2^2} + \frac{1}{3^2} + \dots + \frac{1}{n^2} + \frac{1}{(n+1)^2} &< \frac{n-1}{n} + \frac{1}{(n+1)^2} = \frac{(n-1)(n+1)^2+n}{n(n+1)^2} \\
&= \frac{(n^2-1)(n+1)+n}{n(n+1)^2} = \frac{n^3+n^2-1}{(n^2+n)(n+1)} \\
&< \frac{n^3+n^2}{(n^2+n)(n+1)} = \frac{n(n^2+n)}{(n^2+n)(n+1)}= \frac{(n+1)-1}{n+1}
\end{align*}$[/latex]

8)


Cool



_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. Drzim prodike
[Vrh]
Korisnički profil Pošaljite privatnu poruku
punio4
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: muško
Sarma = la pohva - posuda
3 = 11 - 8
Lokacija: Zagreb
PostPostano: 19:37 sri, 21. 11. 2007    Naslov: Citirajte i odgovorite
Kako si dobio tu desnu stranu?
Kaj nije kada je [latex]n=n+1[/latex] da ispadne:
[latex]\dfrac{(n+1)-1}{n+1}[/latex]?
Kako si dobio tu desnu stranu?
Kaj nije kada je da ispadne:
?


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Masiela
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: žensko
Sarma = la pohva - posuda
74 = 97 - 23
Lokacija: Među bananama
PostPostano: 19:42 sri, 21. 11. 2007    Naslov: Citirajte i odgovorite
Nama je asistentica od samog početka rekla da možemo dirati obje strane, znači recimo cijelu (ne)jednadžbu kvadrirati ili pomnožiti s onim što je u nazivnicima. Bitno je na kraju dobiti nešto što općenito vrijedi. Čak smo to i na vježbama radili tako da nije bila šema da joj je netko došao i rekao kao [i]Ja sam to ovako riješio. Može li se to raditi?[/i] Dakle, pokazano nam je tako.
Nama je asistentica od samog početka rekla da možemo dirati obje strane, znači recimo cijelu (ne)jednadžbu kvadrirati ili pomnožiti s onim što je u nazivnicima. Bitno je na kraju dobiti nešto što općenito vrijedi. Čak smo to i na vježbama radili tako da nije bila šema da joj je netko došao i rekao kao Ja sam to ovako riješio. Može li se to raditi? Dakle, pokazano nam je tako.



_________________
mladac: e.k.s. je možda 8%, moje znanje ni toliko Sad
[Vrh]
Korisnički profil Pošaljite privatnu poruku
anam
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Sarma = la pohva - posuda
-30 = 8 - 38
Lokacija: My Hercegovina!!!!!
PostPostano: 19:44 sri, 21. 11. 2007    Naslov: Citirajte i odgovorite
da evo upravo sam i ja pronašla primjer gdje je kratila lijevu i desnu stranu i kvadrirala ih je obje zajedno
da evo upravo sam i ja pronašla primjer gdje je kratila lijevu i desnu stranu i kvadrirala ih je obje zajedno


[Vrh]
Korisnički profil Pošaljite privatnu poruku
vsego
Site Admin
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: zombi
Sarma = la pohva - posuda
854 = 1068 - 214
Lokacija: /sbin/init
PostPostano: 19:54 sri, 21. 11. 2007    Naslov: Citirajte i odgovorite
[quote="punio4"][latex]n=n+1[/latex][/quote]

NHF, ali ovo je besmisleno. :?

[quote="punio4"][latex]\dfrac{(n+1)-1}{n+1}[/latex]?[/quote]

A sto sam ja dobio? :grebgreb:
punio4 (napisa):


NHF, ali ovo je besmisleno. Confused

punio4 (napisa):
?


A sto sam ja dobio? Kotacici rade 100 na sat



_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. Drzim prodike
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Masiela
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: žensko
Sarma = la pohva - posuda
74 = 97 - 23
Lokacija: Među bananama
PostPostano: 19:57 sri, 21. 11. 2007    Naslov: Citirajte i odgovorite
Da li kolokvije iz EM svaki asistent ispravlja za svoju grupu ili su nekako podijeljeni po zadacima? :neupućena: :D
Da li kolokvije iz EM svaki asistent ispravlja za svoju grupu ili su nekako podijeljeni po zadacima? :neupućena: Very Happy



_________________
mladac: e.k.s. je možda 8%, moje znanje ni toliko Sad
[Vrh]
Korisnički profil Pošaljite privatnu poruku
ß
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 29. 07. 2006. (15:29:06)
Postovi: (115)16
Spol: muško
Sarma = la pohva - posuda
41 = 46 - 5
Lokacija: Graveyard Mountain Home
PostPostano: 21:40 sri, 21. 11. 2007    Naslov: Citirajte i odgovorite
[quote="Masiela"]Da li kolokvije iz EM svaki asistent ispravlja za svoju grupu ili su nekako podijeljeni po zadacima? :neupućena: :D[/quote]

Obično asistenti podijele međusobno (među sobama :) ) zadatke, s tim da često, ukoliko postoje čisto teorijski zadatci, te ispravljaju nastavnici.

Ne vjerujem da postoje podjele s obzirom na grupe studenata, bar ne iz svog skromnog žalbenog iskustva... :D
Masiela (napisa):
Da li kolokvije iz EM svaki asistent ispravlja za svoju grupu ili su nekako podijeljeni po zadacima? :neupućena: Very Happy


Obično asistenti podijele međusobno (među sobama Smile ) zadatke, s tim da često, ukoliko postoje čisto teorijski zadatci, te ispravljaju nastavnici.

Ne vjerujem da postoje podjele s obzirom na grupe studenata, bar ne iz svog skromnog žalbenog iskustva... Very Happy



_________________
Devious movements in your eyes moved me from relief
Breath comes out white clouds with your lies
and filters through me
[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
punio4
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: muško
Sarma = la pohva - posuda
3 = 11 - 8
Lokacija: Zagreb
PostPostano: 22:09 sri, 21. 11. 2007    Naslov: Citirajte i odgovorite
Hm, al ak će bit 12 zadataka, sumnjam da će se pisat na 12 listova papira :\
Hm, al ak će bit 12 zadataka, sumnjam da će se pisat na 12 listova papira :\


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
ma
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: muško
Sarma = la pohva - posuda
58 = 89 - 31
PostPostano: 23:01 sri, 21. 11. 2007    Naslov: Citirajte i odgovorite
[quote="punio4"]Hm, al ak će bit 12 zadataka, sumnjam da će se pisat na 12 listova papira :\[/quote]

neće. sve ćete pisati na njihove papire, a onda će ti papiri kružiti od jednog do drugog asistenta, ovisno o tome tko ispravlja koji zadatak. :D
punio4 (napisa):
Hm, al ak će bit 12 zadataka, sumnjam da će se pisat na 12 listova papira :\


neće. sve ćete pisati na njihove papire, a onda će ti papiri kružiti od jednog do drugog asistenta, ovisno o tome tko ispravlja koji zadatak. Very Happy



_________________
ima let u finish
[Vrh]
Korisnički profil Pošaljite privatnu poruku
finalni
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 04. 08. 2007. (11:48:53)
Postovi: (10D)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
27 = 45 - 18
Lokacija: Bloodbuzz Zagreb
PostPostano: 2:28 pet, 23. 11. 2007    Naslov: Citirajte i odgovorite
[quote="Luuka"]Pretpostavljaš istinitost time kaj napišeš na desnoj strani kaj bi trebo dobit za n+1 ;)
A tek želiš doć do toga...tu formulu dokazat[/quote]

Netočno.
Npr. tvrdnja P(n) za prirodne n neka bude [latex]\sum_{i=1}^n i= \frac{n(n+1)}{2}[/latex].
Ako pretpostavimo da vrijedi P(n) i idemo dokazati P(n+1), zapravo trebamo dokazati
[latex]\sum_{i=1}^{n+1} i= \frac{(n+1)(n+2)}{2}[/latex]
odnosno [latex]\sum_{i=1}^n i + (n+1) = \frac{n^2+3n+2}{2}[/latex]
što je po pretpostavci ekvivalentno s [latex]\frac{n(n+1)}{2}+n+1=\frac{n^2+3n+2}{2}[/latex]
tj. [latex]\frac{n^2+n+2n+2}{2}=\frac{n^2+3n+2}{2}[/latex]
tj. [latex]0=0[/latex].
Nigdje nije prepostavljeno da vrijedi P(n+1), nego je uz pretpostavku da vrijedi P(n) pokazano da je P(n+1) ekvivalentno nečem očitom, tj. dokazano je da [latex]P(n)\Longrightarrow (P(n+1) \Longleftrightarrow 0=0)[/latex].

Ovo totalno podsjeća na http://www.mathlinks.ro/viewtopic.php?p=748796&search_id=1832883536#748796

Matematički rečeno, jednakost je tranzitivna relacija :P
Luuka (napisa):
Pretpostavljaš istinitost time kaj napišeš na desnoj strani kaj bi trebo dobit za n+1 Wink
A tek želiš doć do toga...tu formulu dokazat


Netočno.
Npr. tvrdnja P(n) za prirodne n neka bude .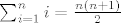
Ako pretpostavimo da vrijedi P(n) i idemo dokazati P(n+1), zapravo trebamo dokazati

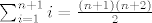
odnosno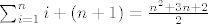
što je po pretpostavci ekvivalentno s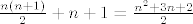
tj.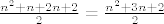
tj. .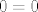
Nigdje nije prepostavljeno da vrijedi P(n+1), nego je uz pretpostavku da vrijedi P(n) pokazano da je P(n+1) ekvivalentno nečem očitom, tj. dokazano je da .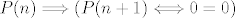

Ovo totalno podsjeća na http://www.mathlinks.ro/viewtopic.php?p=748796&search_id=1832883536#748796

Matematički rečeno, jednakost je tranzitivna relacija Razz



_________________
Nikola Adžaga
Građevinski fakultet, Sveučilište u Zagrebu
[Vrh]
Korisnički profil Pošaljite privatnu poruku
vsego
Site Admin
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: zombi
Sarma = la pohva - posuda
854 = 1068 - 214
Lokacija: /sbin/init
PostPostano: 4:16 pet, 23. 11. 2007    Naslov: Citirajte i odgovorite
[quote="finalni"]Ako pretpostavimo da vrijedi P(n) i idemo dokazati P(n+1), zapravo trebamo dokazati
[latex]\sum_{i=1}^{n+1} i= \frac{(n+1)(n+2)}{2}[/latex]
odnosno [latex]\sum_{i=1}^n i + (n+1) = \frac{n^2+3n+2}{2}[/latex]
što je po pretpostavci [color=red]ekvivalentno[/color] s [latex]\frac{n(n+1)}{2}+n+1=\frac{n^2+3n+2}{2}[/latex]
tj. [latex]\frac{n^2+n+2n+2}{2}=\frac{n^2+3n+2}{2}[/latex]
tj. [latex]0=0[/latex].[/quote]

Mislim da vam upravo zbog ovog "ekvivalentno" brane raditi takve stvari, jer nisu sve operacije "dvosmjerne" (i.e. ponekad imas samo implikaciju). :| Tipican primjer je kvadriranje izraza:
[latex]a = b \Rightarrow a^2 = b^2[/latex]
Obrato, ocito, ne vrijedi. ;)

Ti ovdje nisi pretpostavio da tvrdnja vrijedi za n+1, nego si povlacio ekvivalencije: "tvrdnja vrijedi za n+1 akko..., a to onda akko..." ;)

Zato se pribjegava necem drugom:
[latex]a_{n+1} = f(n+1) \Leftrightarrow a_{n+1} - f(n+1) = 0[/latex]
pa se stvar svodi na racunanje razlike (koja treba ispasti nula). :D Time koristite sve blagodati jednakosti bez da ste explicite pretpostavili da ona vrijedi. ;)
finalni (napisa):
Ako pretpostavimo da vrijedi P(n) i idemo dokazati P(n+1), zapravo trebamo dokazati

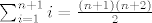
odnosno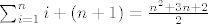
što je po pretpostavci ekvivalentno s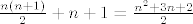
tj.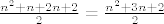
tj. .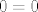


Mislim da vam upravo zbog ovog "ekvivalentno" brane raditi takve stvari, jer nisu sve operacije "dvosmjerne" (i.e. ponekad imas samo implikaciju). Neutral Tipican primjer je kvadriranje izraza:

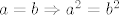
Obrato, ocito, ne vrijedi. Wink

Ti ovdje nisi pretpostavio da tvrdnja vrijedi za n+1, nego si povlacio ekvivalencije: "tvrdnja vrijedi za n+1 akko..., a to onda akko..." Wink

Zato se pribjegava necem drugom:

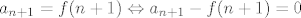
pa se stvar svodi na racunanje razlike (koja treba ispasti nula). Very Happy Time koristite sve blagodati jednakosti bez da ste explicite pretpostavili da ona vrijedi. Wink



_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. Drzim prodike
[Vrh]
Korisnički profil Pošaljite privatnu poruku
finalni
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 04. 08. 2007. (11:48:53)
Postovi: (10D)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
27 = 45 - 18
Lokacija: Bloodbuzz Zagreb
PostPostano: 14:42 pet, 23. 11. 2007    Naslov: Citirajte i odgovorite
[quote="vsego"]
Mislim da vam upravo zbog ovog "ekvivalentno" brane raditi takve stvari, jer nisu sve operacije "dvosmjerne" (i.e. ponekad imas samo implikaciju). :| Tipican primjer je kvadriranje izraza:
[latex]a = b \Rightarrow a^2 = b^2[/latex]
Obrato, ocito, ne vrijedi. ;)[/quote]

Ali one primijenjene jesu! :evil: :D :)

[quote]Ti ovdje nisi pretpostavio da tvrdnja vrijedi za n+1, nego si povlacio ekvivalencije: "tvrdnja vrijedi za n+1 akko..., a to onda akko..." ;)

Zato se pribjegava necem drugom:
[latex]a_{n+1} = f(n+1) \Leftrightarrow a_{n+1} - f(n+1) = 0[/latex]
pa se stvar svodi na racunanje razlike (koja treba ispasti nula). :D Time koristite sve blagodati jednakosti bez da ste explicite pretpostavili da ona vrijedi. ;)[/quote]

Baš sam mislio napisati da se može jednostavno napisati da treba dokazati [latex]\sum_{i=1}^{n} i - \frac{n(n+1)}{2}=0[/latex] pa je onda očito da smijemo "dirati obje strane" u onoj prvoj tvrdnji jer inače bismo u ovoj smjeli mijenjati samo prvu polovicu lijeve strane.

Obično je jednostavnije i brže računati obje strane nego pokušavati svesti jednu na drugu (što je nekad teško izvedivo i totalno neprirodno).

A o čem mi raspravljamo. :D

Vezano za indukciju, na kolokviju je bio samo jedan zadatak, i to s djeljivošću, a mogao se i bez indukcije riješiti. :)
vsego (napisa):

Mislim da vam upravo zbog ovog "ekvivalentno" brane raditi takve stvari, jer nisu sve operacije "dvosmjerne" (i.e. ponekad imas samo implikaciju). Neutral Tipican primjer je kvadriranje izraza:

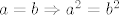
Obrato, ocito, ne vrijedi. Wink


Ali one primijenjene jesu! Evil or Very Mad Very Happy Smile

Citat:
Ti ovdje nisi pretpostavio da tvrdnja vrijedi za n+1, nego si povlacio ekvivalencije: "tvrdnja vrijedi za n+1 akko..., a to onda akko..." Wink

Zato se pribjegava necem drugom:

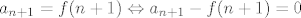
pa se stvar svodi na racunanje razlike (koja treba ispasti nula). Very Happy Time koristite sve blagodati jednakosti bez da ste explicite pretpostavili da ona vrijedi. Wink


Baš sam mislio napisati da se može jednostavno napisati da treba dokazati 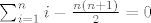pa je onda očito da smijemo "dirati obje strane" u onoj prvoj tvrdnji jer inače bismo u ovoj smjeli mijenjati samo prvu polovicu lijeve strane.

Obično je jednostavnije i brže računati obje strane nego pokušavati svesti jednu na drugu (što je nekad teško izvedivo i totalno neprirodno).

A o čem mi raspravljamo. Very Happy

Vezano za indukciju, na kolokviju je bio samo jedan zadatak, i to s djeljivošću, a mogao se i bez indukcije riješiti. Smile



_________________
Nikola Adžaga
Građevinski fakultet, Sveučilište u Zagrebu
[Vrh]
Korisnički profil Pošaljite privatnu poruku
ivica13
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 03. 10. 2007. (14:01:02)
Postovi: (102)16
Spol: muško
Sarma = la pohva - posuda
67 = 75 - 8
PostPostano: 17:50 uto, 4. 12. 2007    Naslov: Citirajte i odgovorite
Jel netko dokazao 5. zadatak...
[latex]
1/1 + 1/2 + ... + 1/n >= 2n/(n+1)
[/latex]

unaprijed hvala dobrim dušama...
Jel netko dokazao 5. zadatak...


unaprijed hvala dobrim dušama...


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 18:38 uto, 4. 12. 2007    Naslov: Citirajte i odgovorite
Vrlo lijepa indukcija...
baza ok ( 1>=1)
prep je to što ti piše da vrijedi za neki n iz N.
Sad korak:

[latex]\sum_{k=1}^{n+1}{\frac{1}{k}} = \sum_{k=1}^{n}{\frac{1}{k}}+ \frac {1}{n+1} \geq \frac{2n}{n+1} + \frac{1}{n+1} = \frac{2n+1}{n+1} \geq \frac{2n+2}{n+2}[/latex]

Ovo zadnje lako provjeriš...sve ti je pozitivno jer je n iz N pa smiješ množit nejednakost pa se dobije da je n>=0 što je.
Vrlo lijepa indukcija...
baza ok ( 1>=1)
prep je to što ti piše da vrijedi za neki n iz N.
Sad korak:



Ovo zadnje lako provjeriš...sve ti je pozitivno jer je n iz N pa smiješ množit nejednakost pa se dobije da je n>=0 što je.



_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Elementarna matematika 1 i 2 Vremenska zona: GMT + 01:00.
Idite na Prethodno  1, 2
Stranica 2 / 2.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan