| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
desire
Forumaš(ica)
Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
matmih
Forumaš(ica)
Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
 Postano: 21:11 ned, 3. 2. 2008 Naslov: |
    |
|
|
[quote="Luuka"]2. reko bi da je K unutar R2. A to pokažeš ovak: ideš tražit stac točke na stand način i vj se dobije da su sedlo. Pa ti kažeš da pošto je K kompaktan, f nepr da se mora dostić minimum i maksimum. Pošto to nije postigla na IntK (nije na nijednom otv skupu, pa ni na najvećem mogućem) onda se min i max postižu na rubu od K.[/quote]
Nažalost dobije se da je [latex] (\sqrt{2},- \sqrt{2})[/latex] lokalni minimum, i sada se postavlja pitanje kako dokazati da je on točno na rubu tog skupa ili kako dokazati da na rubu postoji manji od njega.
@desire, imam jedno 3-4 pokušaja od kojih svaki dođe drugačije, i svaki je dosta dugačak. :lol:
Dakle ne još nisam 100% skužio kako to rješit.
Kolko tebi dođe?
| Luuka (napisa): | | 2. reko bi da je K unutar R2. A to pokažeš ovak: ideš tražit stac točke na stand način i vj se dobije da su sedlo. Pa ti kažeš da pošto je K kompaktan, f nepr da se mora dostić minimum i maksimum. Pošto to nije postigla na IntK (nije na nijednom otv skupu, pa ni na najvećem mogućem) onda se min i max postižu na rubu od K. |
Nažalost dobije se da je 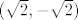 lokalni minimum, i sada se postavlja pitanje kako dokazati da je on točno na rubu tog skupa ili kako dokazati da na rubu postoji manji od njega.
@desire, imam jedno 3-4 pokušaja od kojih svaki dođe drugačije, i svaki je dosta dugačak. 
Dakle ne još nisam 100% skužio kako to rješit.
Kolko tebi dođe?
|
|
| [Vrh] |
|
desire
Forumaš(ica)
Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol:
|
|
| [Vrh] |
|
betty
Forumaš(ica)
Pridružen/a: 23. 02. 2006. (19:17:18)
Postovi: (2D)16
|
|
| [Vrh] |
|
sun
Forumaš(ica)
Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol:
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)
Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol:
Lokacija: |R^3
|
|
| [Vrh] |
|
Fisher
Forumaš(ica)
Pridružen/a: 09. 02. 2007. (23:38:24)
Postovi: (41)16
Lokacija: split
|
|
| [Vrh] |
|
napraviculom
Forumaš(ica)
Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol:
Lokacija: Scranton
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Fisher
Forumaš(ica)
Pridružen/a: 09. 02. 2007. (23:38:24)
Postovi: (41)16
Lokacija: split
|
|
| [Vrh] |
|
napraviculom
Forumaš(ica)
Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol:
Lokacija: Scranton
|
|
| [Vrh] |
|
matmih
Forumaš(ica)
Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol:
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
ma
Forumaš(ica)
Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol:
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
| Postano: 15:26 pon, 4. 2. 2008 Naslov: |
|
|
|
Nije vezano za temu, al ovo je izgleda topic za pitanja, pa da i ja nešt pitam.
Prošlogodišnji kolokvij ([url=http://web.math.hr/nastava/difraf/dif/2006-07/kolokvij_2.pdf]link[/url]), 4.zadatak.
Jel tu treba samo definirat neku novu fju sa R3 u R2 (f) i reć da je g=F o f.
Pošto je F difb, a i ta f koju definiramo (jel to treba dokazat) onda je difb i g kao njihova kompozicija i Dg(x,y,z)=DF(x,y)*Df(x,y,z) ?
Nije vezano za temu, al ovo je izgleda topic za pitanja, pa da i ja nešt pitam.
Prošlogodišnji kolokvij (link), 4.zadatak.
Jel tu treba samo definirat neku novu fju sa R3 u R2 (f) i reć da je g=F o f.
Pošto je F difb, a i ta f koju definiramo (jel to treba dokazat) onda je difb i g kao njihova kompozicija i Dg(x,y,z)=DF(x,y)*Df(x,y,z) ?
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)
Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol:
Lokacija: |R^3
|
| Postano: 15:38 pon, 4. 2. 2008 Naslov: |
|
|
|
[quote="Luuka"]
Prošlogodišnji kolokvij ([url=http://web.math.hr/nastava/difraf/dif/2006-07/kolokvij_2.pdf]link[/url]), 4.zadatak.
Jel tu treba samo definirat neku novu fju sa R3 u R2 (f) i reć da je g=F o f.[/quote]
Tako je.
[quote]
Pošto je F difb, a i ta f koju definiramo (jel to treba dokazat)[/quote]
Trivijalno se vidi da je ta nova f dfb(njene su komponentne funkcije dfb funkcije(jer su koordinatne projekcije dfb funkcije i jer je linearna kombinacija i kompozicija dfb funkcija dfb funkcija)). To svakako vrijedi zapisati, ne košta mnogo vremena, tek zerce tinte.
[quote] onda je difb i g kao njihova kompozicija i Dg(x,y,z)=DF(x,y)*Df(x,y,z) ?[/quote]
Tako je. S obzirom da je dano djelovanje funkcije f, imaš njenu Jacobijevu matricu pa ovu gore kompoziciju diferencijala možeš identificirati (Jacobijevim) matricama i tako, dakle matrično, zapisati traženi diferencijal.
| Luuka (napisa): |
Prošlogodišnji kolokvij (link), 4.zadatak.
Jel tu treba samo definirat neku novu fju sa R3 u R2 (f) i reć da je g=F o f. |
Tako je.
| Citat: |
Pošto je F difb, a i ta f koju definiramo (jel to treba dokazat) |
Trivijalno se vidi da je ta nova f dfb(njene su komponentne funkcije dfb funkcije(jer su koordinatne projekcije dfb funkcije i jer je linearna kombinacija i kompozicija dfb funkcija dfb funkcija)). To svakako vrijedi zapisati, ne košta mnogo vremena, tek zerce tinte.
| Citat: | | onda je difb i g kao njihova kompozicija i Dg(x,y,z)=DF(x,y)*Df(x,y,z) ? |
Tako je. S obzirom da je dano djelovanje funkcije f, imaš njenu Jacobijevu matricu pa ovu gore kompoziciju diferencijala možeš identificirati (Jacobijevim) matricama i tako, dakle matrično, zapisati traženi diferencijal.
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)
Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol:
Lokacija: |R^3
|
| Postano: 15:44 pon, 4. 2. 2008 Naslov: |
|
|
|
Mene mori zadatak sa vježbi:
Ispitajte dfb funkcije
f(x,y) = (xy)/sqrt(x^2 + y^2) za (x,y) != (0,0)
f(x,y) = 0 za (x,y)=(0,0)
I sada, da ne raspisujem, se dfb ispituje na već mnogo puta viđen način.. u jednom trenutku se ispituje dfb funkcije u točki (0,0) gdje je kandidat za diferencijal nul-funkcional(razumljivo ako se odrede parcijalne derivacije u (0,0) ) pa limes izgleda ovako:
lim_{(x,y)->(0,0)} (f(x,y)-f(0,0))/sqrt(x^2 + y^2)
Pitanje glasi:
Gdje je nestala norma u brojniku limesa? (ona svakako postoji u definiciji dfb-sti u točki)
Mene mori zadatak sa vježbi:
Ispitajte dfb funkcije
f(x,y) = (xy)/sqrt(x^2 + y^2) za (x,y) != (0,0)
f(x,y) = 0 za (x,y)=(0,0)
I sada, da ne raspisujem, se dfb ispituje na već mnogo puta viđen način.. u jednom trenutku se ispituje dfb funkcije u točki (0,0) gdje je kandidat za diferencijal nul-funkcional(razumljivo ako se odrede parcijalne derivacije u (0,0) ) pa limes izgleda ovako:
lim_{(x,y)->(0,0)} (f(x,y)-f(0,0))/sqrt(x^2 + y^2)
Pitanje glasi:
Gdje je nestala norma u brojniku limesa? (ona svakako postoji u definiciji dfb-sti u točki)
|
|
| [Vrh] |
|
Raz
Forumaš(ica)
Pridružen/a: 07. 02. 2005. (22:40:23)
Postovi: (6F)16
Lokacija: Tamo gdje ribe jedu avanturiste...
|
| Postano: 16:05 pon, 4. 2. 2008 Naslov: |
|
|
|
[quote="noa"]kako9.zad u 3. zadaci?
nadem Df al sto s tockama koje nisu u domeni??
i kako dokazujem da je neka fja neprekidna znam dokazati da nije neprekidna ali kako da je? po def?? ili?mislim kada ne ide po onom da lim(X,Y)->tu tocku.....[/quote]
ne znam na koju 3. zadacu mislis jer ih ima vise oznacenih sa 3. al... pretp. da je neprekidnost fje u(1,0)...?
dakle... gledas dali postoji lim kad (x,y)->(1,0) i dal je jednak f(1,0)=0
to mozes gledat kao funkciju jedne varijable ili preko polarnih kordinata
| noa (napisa): | kako9.zad u 3. zadaci?
nadem Df al sto s tockama koje nisu u domeni??
i kako dokazujem da je neka fja neprekidna znam dokazati da nije neprekidna ali kako da je? po def?? ili?mislim kada ne ide po onom da lim(X,Y)→tu tocku..... |
ne znam na koju 3. zadacu mislis jer ih ima vise oznacenih sa 3. al... pretp. da je neprekidnost fje u(1,0)...?
dakle... gledas dali postoji lim kad (x,y)→(1,0) i dal je jednak f(1,0)=0
to mozes gledat kao funkciju jedne varijable ili preko polarnih kordinata
_________________
One good thing about music,when it hits: you feel no pain
|
|
| [Vrh] |
|
|
