Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

Šesta domaća zadaća (zadatak)
WWW:
Idite na Prethodno  1, 2
Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Elementarna matematika 1 i 2
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
punio4
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: muško
Sarma = la pohva - posuda
3 = 11 - 8
Lokacija: Zagreb
PostPostano: 17:55 sri, 6. 2. 2008    Naslov: Citirajte i odgovorite
[quote="ma"][quote="punio4"]No zapeo sam na trećem... Može pomoć :) ?
Dakle imamo neki polinom oblika:
[latex]f(x)=a_n x^n + a_{n-1}x^{n-1}\ldots+a_1 x + a_0[/latex]
[latex]g(x)=x^2-1[/latex]
I vrijedi iduće:
[latex]a_1+\ldots + a_n = 2[/latex]
[latex]a_1+a_3+\ldots+a_{2n-1}=a_2+a_4+\ldots+a_{2n}[/latex]
Traži se ostatak pri dijeljenju polinoma, [latex]r(x)[/latex].[/quote]

ne treba ti horner :P

to ti je super primjer za ono što si pitao - gdje nam pomažu nultočke polinoma kojim dijelimo :D

imaš: [latex]f(x) = q(x) \cdot g(x) + r(x)[/latex].
sada lijepo uvrstiš nultočke od g u jednadžbu - time ćeš ubiti q(x) (polinom koji smo dobili dijeljenjem f sa g, a koji ne znamo, niti trebamo znati). s obzirom da su nultočke od g tako lijepe, koristeći dodatne jednakosti iz zadatka dobit ćeš čemu je jednak ostatak (on je, za početak, polinom najviše stupnja 1). :wink:

:rakun:[/quote]
Ok, nultočke od g(x) su 1 i -1.
Dobijemo:
[latex]f(1)=a+b\Rightarrow a_0+(a_1+\ldots+a_n)=a+b\Rightarrow a_0+2=a+b[/latex]
[latex]f(-1)=-a+b\Rightarrow a_0+(-a_1-\ldots-a_n)=-a+b\Rightarrow a_0-2=-a+b[/latex]
Tu sam upotrijebio onaj [latex]a_1+\ldots + a_n = 2[/latex]
Sad kako upotrijebiti [latex]a_1+a_3+\ldots+a_{2n-1}=a_2+a_4+\ldots+a_{2n}[/latex]?
ma (napisa):
punio4 (napisa):
No zapeo sam na trećem... Može pomoć Smile ?
Dakle imamo neki polinom oblika:


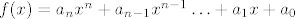
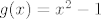
I vrijedi iduće:


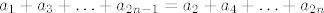
Traži se ostatak pri dijeljenju polinoma, .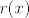


ne treba ti horner Razz

to ti je super primjer za ono što si pitao - gdje nam pomažu nultočke polinoma kojim dijelimo Very Happy

imaš: .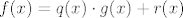
sada lijepo uvrstiš nultočke od g u jednadžbu - time ćeš ubiti q(x) (polinom koji smo dobili dijeljenjem f sa g, a koji ne znamo, niti trebamo znati). s obzirom da su nultočke od g tako lijepe, koristeći dodatne jednakosti iz zadatka dobit ćeš čemu je jednak ostatak (on je, za početak, polinom najviše stupnja 1). Wink

Rakun Koji Pleshe

Ok, nultočke od g(x) su 1 i -1.
Dobijemo:


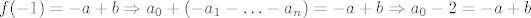
Tu sam upotrijebio onaj
Sad kako upotrijebiti ?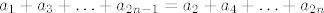


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
ma
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: muško
Sarma = la pohva - posuda
58 = 89 - 31
PostPostano: 18:07 sri, 6. 2. 2008    Naslov: Citirajte i odgovorite
[quote="punio4"][latex]f(-1)=-a+b\Rightarrow a_0+(-a_1-\ldots-a_n)=-a+b\Rightarrow a_0-2=-a+b[/latex][/quote]

ajde još jednom :rakun:
punio4 (napisa):


ajde još jednom Rakun Koji Pleshe



_________________
ima let u finish
[Vrh]
Korisnički profil Pošaljite privatnu poruku
punio4
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: muško
Sarma = la pohva - posuda
3 = 11 - 8
Lokacija: Zagreb
PostPostano: 18:15 sri, 6. 2. 2008    Naslov: Citirajte i odgovorite
A~HA!
[latex]f(-1)=a_0-a_1+a_2-a_3+\ldots-a_{2n-1}+a_{2n}=-a+b[/latex]
[latex]f(-1)=a_0=-a+b[/latex]?
A~HA!

?


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
ma
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: muško
Sarma = la pohva - posuda
58 = 89 - 31
PostPostano: 18:23 sri, 6. 2. 2008    Naslov: Citirajte i odgovorite
[quote="punio4"]A~HA!
[latex]f(-1)=a_0-a_1+a_2-a_3+\ldots-a_{2n-1}+a_{2n}=-a+b[/latex]
[latex]f(-1)=a_0=-a+b[/latex]?[/quote]

bolje je. sad idi do kraja. riješi sustav.
punio4 (napisa):
A~HA!

?


bolje je. sad idi do kraja. riješi sustav.



_________________
ima let u finish
[Vrh]
Korisnički profil Pošaljite privatnu poruku
punio4
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: muško
Sarma = la pohva - posuda
3 = 11 - 8
Lokacija: Zagreb
PostPostano: 18:35 sri, 6. 2. 2008    Naslov: Citirajte i odgovorite
Jej! a i b su 1!
Hvala ma.
Još samo... 8 zadataka :(
Jej! a i b su 1!
Hvala ma.
Još samo... 8 zadataka Sad


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
k8yvis
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 10. 2006. (14:32:30)
Postovi: (79)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
-36 = 8 - 44
PostPostano: 18:55 sri, 6. 2. 2008    Naslov: Citirajte i odgovorite
Piši, rješit ćemo.
Piši, rješit ćemo.



_________________
Da li je napredak kad ljudozder uzme vilicu?
[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
punio4
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: muško
Sarma = la pohva - posuda
3 = 11 - 8
Lokacija: Zagreb
PostPostano: 19:17 sri, 6. 2. 2008    Naslov: Citirajte i odgovorite
4. neću ni razmišljat...
Kako bi 5. išao? Da napišem zadatak cijeli tu?
4. neću ni razmišljat...
Kako bi 5. išao? Da napišem zadatak cijeli tu?


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
k8yvis
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 10. 2006. (14:32:30)
Postovi: (79)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
-36 = 8 - 44
PostPostano: 19:29 sri, 6. 2. 2008    Naslov: Citirajte i odgovorite
a, gle, ja nemam tvoju zadaću... Pa bi možda i mogao..
a, gle, ja nemam tvoju zadaću... Pa bi možda i mogao..



_________________
Da li je napredak kad ljudozder uzme vilicu?
[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
punio4
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: muško
Sarma = la pohva - posuda
3 = 11 - 8
Lokacija: Zagreb
PostPostano: 19:35 sri, 6. 2. 2008    Naslov: Citirajte i odgovorite
Aaa, moje isprike. Dakle, zadatak:

Odredite polinom trećeg stupnja s vodećim koeficijentom 4 ako njegove nultočke [latex]x_1, x_2, x_3[/latex] zadovoljavaju nejednakosti:
[latex]\dfrac{1}{x_1}+\dfrac{1}{x_2}+\dfrac{1}{x_3}=2[/latex]
[latex]\dfrac{1}{x_1 x_2}+\dfrac{1}{x_1 x_3}+\dfrac{1}{x_2 x_3}=8[/latex]
[latex]\dfrac{1}{x_1 x_2 x_3}=8[/latex]
Aaa, moje isprike. Dakle, zadatak:

Odredite polinom trećeg stupnja s vodećim koeficijentom 4 ako njegove nultočke zadovoljavaju nejednakosti:




[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
k8yvis
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 10. 2006. (14:32:30)
Postovi: (79)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
-36 = 8 - 44
PostPostano: 19:47 sri, 6. 2. 2008    Naslov: Citirajte i odgovorite
Cilj ti je riješiti tri jednadžbe s tri nepoznanice (primjeti da je 8=8 pa i lijeve strane tu možeš izjednačit) i pazi kako se riješavaš nazivnika. Kad dobiješ x1,x2 i x3 onda samo vidi attach gdje su x1,x2,...,xn nultočke polinoma.
Cilj ti je riješiti tri jednadžbe s tri nepoznanice (primjeti da je 8=8 pa i lijeve strane tu možeš izjednačit) i pazi kako se riješavaš nazivnika. Kad dobiješ x1,x2 i x3 onda samo vidi attach gdje su x1,x2,...,xn nultočke polinoma.



_________________
Da li je napredak kad ljudozder uzme vilicu?
[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
Lafiel
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: žensko
Sarma = la pohva - posuda
27 = 51 - 24
PostPostano: 20:06 sri, 6. 2. 2008    Naslov: Citirajte i odgovorite
[quote="punio4"]No zapeo sam na trećem... Može pomoć :) ?
Dakle imamo neki polinom oblika:
[latex]f(x)=a_n x^n + a_{n-1}x^{n-1}\ldots+a_1 x + a_0[/latex]
[latex]g(x)=x^2-1[/latex]
I vrijedi iduće:
[latex]a_1+\ldots + a_n = 2[/latex]
[latex]a_1+a_3+\ldots+a_{2n-1}=a_2+a_4+\ldots+a_{2n}[/latex]
Traži se ostatak pri dijeljenju polinoma, [latex]r(x)[/latex].[/quote]
Umm, ovo će možda zvučati glupo, ali zašto pod "koeficijenti" (dakle, "zbroj koeficijenata") ne računamo i [latex]a_0[/latex]? [img]http://i2.photobucket.com/albums/y29/waterfly89/Smilies/unsure.gif[/img]
punio4 (napisa):
No zapeo sam na trećem... Može pomoć Smile ?
Dakle imamo neki polinom oblika:


I vrijedi iduće:


Traži se ostatak pri dijeljenju polinoma, .

Umm, ovo će možda zvučati glupo, ali zašto pod "koeficijenti" (dakle, "zbroj koeficijenata") ne računamo i ?



_________________
Weit von hier fällt Gold von den Sternen
[Vrh]
Korisnički profil Pošaljite privatnu poruku
punio4
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: muško
Sarma = la pohva - posuda
3 = 11 - 8
Lokacija: Zagreb
PostPostano: 20:10 sri, 6. 2. 2008    Naslov: Citirajte i odgovorite
Nije bilo navedeno eksplicitno "uključujući i slobodne koeficijente" pa idemo linijom manjeg otpora :roll:
Nije bilo navedeno eksplicitno "uključujući i slobodne koeficijente" pa idemo linijom manjeg otpora Rolling Eyes


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
mocibob
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 03. 2007. (10:26:53)
Postovi: (16)16
Sarma = la pohva - posuda
0 = 0 - 0
PostPostano: 22:34 sri, 6. 2. 2008    Naslov: khm... Citirajte i odgovorite
zna li mozda netko mozemo li sutra na kolokviju predati zadnje dvije zadace?? (grupa sam od m-r)
zna li mozda netko mozemo li sutra na kolokviju predati zadnje dvije zadace?? (grupa sam od m-r)


[Vrh]
Korisnički profil Pošaljite privatnu poruku
ma
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: muško
Sarma = la pohva - posuda
58 = 89 - 31
PostPostano: 0:25 čet, 7. 2. 2008    Naslov: Citirajte i odgovorite
[quote="punio4"]Odredite polinom trećeg stupnja s vodećim koeficijentom 4 ako njegove nultočke [latex]x_1, x_2, x_3[/latex] zadovoljavaju nejednakosti:
[latex]\dfrac{1}{x_1}+\dfrac{1}{x_2}+\dfrac{1}{x_3}=2[/latex]
[latex]\dfrac{1}{x_1 x_2}+\dfrac{1}{x_1 x_3}+\dfrac{1}{x_2 x_3}=8[/latex]
[latex]\dfrac{1}{x_1 x_2 x_3}=8[/latex][/quote]

[quote="k8yvis"]Cilj ti je riješiti tri jednadžbe s tri nepoznanice (primjeti da je 8=8 pa i lijeve strane tu možeš izjednačit) i pazi kako se riješavaš nazivnika. Kad dobiješ x1,x2 i x3 onda samo vidi attach gdje su x1,x2,...,xn nultočke polinoma.[/quote]

:-k ne baš. loš pristup. ovdje očigledno treba koristiti vietéove formule. :)
punio4 (napisa):
Odredite polinom trećeg stupnja s vodećim koeficijentom 4 ako njegove nultočke 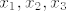zadovoljavaju nejednakosti:




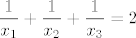
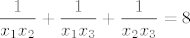
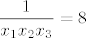k8yvis (napisa):
Cilj ti je riješiti tri jednadžbe s tri nepoznanice (primjeti da je 8=8 pa i lijeve strane tu možeš izjednačit) i pazi kako se riješavaš nazivnika. Kad dobiješ x1,x2 i x3 onda samo vidi attach gdje su x1,x2,...,xn nultočke polinoma.


Think ne baš. loš pristup. ovdje očigledno treba koristiti vietéove formule. Smile



_________________
ima let u finish
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Masiela
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: žensko
Sarma = la pohva - posuda
74 = 97 - 23
Lokacija: Među bananama
PostPostano: 0:31 čet, 7. 2. 2008    Naslov: Citirajte i odgovorite
Da, Viete.

Iz zadnje se dobije x1x2x3.

U drugoj svesti na zajednički nazivnik pa pošto se zna koliko je x1x2x3 se dobije koliko je x1+x2+x3.

U prvoj isto na zajednički nazivnik i dobije se koliko je x1x2+x1x3+x2x3.

Primjeniti Vieteove fomule i to je to.
Da, Viete.

Iz zadnje se dobije x1x2x3.

U drugoj svesti na zajednički nazivnik pa pošto se zna koliko je x1x2x3 se dobije koliko je x1+x2+x3.

U prvoj isto na zajednički nazivnik i dobije se koliko je x1x2+x1x3+x2x3.

Primjeniti Vieteove fomule i to je to.



_________________
mladac: e.k.s. je možda 8%, moje znanje ni toliko Sad
[Vrh]
Korisnički profil Pošaljite privatnu poruku
k8yvis
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 10. 2006. (14:32:30)
Postovi: (79)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
-36 = 8 - 44
PostPostano: 11:36 čet, 7. 2. 2008    Naslov: Citirajte i odgovorite
Ne ograđujem se, samo kažem što je: Pokušavala sam pomoć, međutim, ne znam dokle ste došli, znam jedino da se radi polinome. Iz tog razloga sam pokušavala dati što jednostavnija riješenja. Jednostavnije je s Viete-om, u svakom slučaju, ali ni ovako nije neriješivo.
Ne ograđujem se, samo kažem što je: Pokušavala sam pomoć, međutim, ne znam dokle ste došli, znam jedino da se radi polinome. Iz tog razloga sam pokušavala dati što jednostavnija riješenja. Jednostavnije je s Viete-om, u svakom slučaju, ali ni ovako nije neriješivo.



_________________
Da li je napredak kad ljudozder uzme vilicu?
[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Elementarna matematika 1 i 2 Vremenska zona: GMT + 01:00.
Idite na Prethodno  1, 2
Stranica 2 / 2.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan