| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
sun
Forumaš(ica)

Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol: 
|
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 14:18 ned, 17. 2. 2008 Naslov: Postano: 14:18 ned, 17. 2. 2008 Naslov: |
    |
|
|
I ja mislim da je ok, samo se treba 'razbit' f na komponente pa onda za sve posebno gledat...a kak se razbija f tak razbiješ i A, na retke (njih je m). Sad vrijedi
fi(y)-fi(x)=Ai(y-x) i=1,2,..,m
gdje i označava i-tu komponentu fje f, tj i-ti redak od A.
Na ovaj način se dobije komponenta vektora b (onak kak si napiso fi(y)-Ai(y)=fi(x)-Ai(x)=bi ) pa sve to spojiš u b. 8)
Ak sam negdje fulo, nek me netko ispravi :)
I ja mislim da je ok, samo se treba 'razbit' f na komponente pa onda za sve posebno gledat...a kak se razbija f tak razbiješ i A, na retke (njih je m). Sad vrijedi
fi(y)-fi(x)=Ai(y-x) i=1,2,..,m
gdje i označava i-tu komponentu fje f, tj i-ti redak od A.
Na ovaj način se dobije komponenta vektora b (onak kak si napiso fi(y)-Ai(y)=fi(x)-Ai(x)=bi ) pa sve to spojiš u b. 
Ak sam negdje fulo, nek me netko ispravi 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Blah
Forumaš(ica)

Pridružen/a: 11. 09. 2006. (18:07:56)
Postovi: (C1)16
Spol: 
|
 Postano: 18:18 ned, 17. 2. 2008 Naslov: Postano: 18:18 ned, 17. 2. 2008 Naslov: |
    |
|
|
Ideja za g(r,fi,z)=f(rcos(fi),rsin(fi),z),pokazat diferencijabilnost u (2,pi,1)?
Isto ACR^n , f:A->R^m - Ako A kompaktan da li je f(A) kompaktan i obrat? Hvala!
Ideja za g(r,fi,z)=f(rcos(fi),rsin(fi),z),pokazat diferencijabilnost u (2,pi,1)?
Isto ACR^n , f:A->R^m - Ako A kompaktan da li je f(A) kompaktan i obrat? Hvala!
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:26 ned, 17. 2. 2008 Naslov: Postano: 18:26 ned, 17. 2. 2008 Naslov: |
    |
|
|
[quote="Blah"]Ideja za g(r,fi,z)=f(rcos(fi),rsin(fi),z),pokazat diferencijabilnost u (2,pi,1)?[/quote]
Kako je definirana f ?
[quote="Blah"]
Isto ACR^n , f:A->R^m - Ako A kompaktan da li je f(A) kompaktan i obrat? Hvala![/quote]
A komp -> f(A) kompaktan imaš u skripti.
Obrat općenito ne vrijedi. Kontraprimjer:
f:Rn->Rm
f(x)=2 , za svaki x (ovaj 2 je iz Rm, dakle (2,2,2,...,2) )
f(Rn)=2 što je kompaktan skup (zatv i omeđen) a Rn nije kompaktan (jer nije omeđen)
| Blah (napisa): | | Ideja za g(r,fi,z)=f(rcos(fi),rsin(fi),z),pokazat diferencijabilnost u (2,pi,1)? |
Kako je definirana f ?
| Blah (napisa): |
Isto ACR^n , f:A→R^m - Ako A kompaktan da li je f(A) kompaktan i obrat? Hvala! |
A komp → f(A) kompaktan imaš u skripti.
Obrat općenito ne vrijedi. Kontraprimjer:
f:Rn→Rm
f(x)=2 , za svaki x (ovaj 2 je iz Rm, dakle (2,2,2,...,2) )
f(Rn)=2 što je kompaktan skup (zatv i omeđen) a Rn nije kompaktan (jer nije omeđen)
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
buzov5
Forumaš(ica)

Pridružen/a: 01. 12. 2006. (13:30:32)
Postovi: (4D)16
Lokacija: zg
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 18:52 ned, 17. 2. 2008 Naslov: Postano: 18:52 ned, 17. 2. 2008 Naslov: |
    |
|
|
[quote="Blah"]Ideja za g(r,fi,z)=f(rcos(fi),rsin(fi),z),pokazat diferencijabilnost u (2,pi,1)?
Isto ACR^n , f:A->R^m - Ako A kompaktan da li je f(A) kompaktan i obrat? Hvala![/quote]
mislim da treba definirati funkciju [latex]h(r,\phi,z)=(r\cdot\cos\phi,r\cdot\sin\phi,z)[/latex], pa se igrati majstora kompozicije.
[latex]g=f\circ h[/latex]
| Blah (napisa): | Ideja za g(r,fi,z)=f(rcos(fi),rsin(fi),z),pokazat diferencijabilnost u (2,pi,1)?
Isto ACR^n , f:A→R^m - Ako A kompaktan da li je f(A) kompaktan i obrat? Hvala! |
mislim da treba definirati funkciju 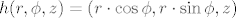 , pa se igrati majstora kompozicije. , pa se igrati majstora kompozicije.
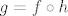
_________________
ima let u finish
Zadnja promjena: ma; 18:54 ned, 17. 2. 2008; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:53 ned, 17. 2. 2008 Naslov: Postano: 18:53 ned, 17. 2. 2008 Naslov: |
    |
|
|
definiram fju h:R3->R3
h(r,fi,z)=(rcos(fi),rsin(fi),z)
Sad je g=foh
h je difb, f je difb pa je i foh (g) difb (svuda) i vrijedi:
Dg(T)=Df(h(T)) Dh(T) , T iz R3.
Time je dokazana difb, još se može izračunat Dh(2,pi,1)...
edit: prestigo me ma... :)
definiram fju h:R3->R3
h(r,fi,z)=(rcos(fi),rsin(fi),z)
Sad je g=foh
h je difb, f je difb pa je i foh (g) difb (svuda) i vrijedi:
Dg(T)=Df(h(T)) Dh(T) , T iz R3.
Time je dokazana difb, još se može izračunat Dh(2,pi,1)...
edit: prestigo me ma... 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Blah
Forumaš(ica)

Pridružen/a: 11. 09. 2006. (18:07:56)
Postovi: (C1)16
Spol: 
|
|
| [Vrh] |
|
Blah
Forumaš(ica)

Pridružen/a: 11. 09. 2006. (18:07:56)
Postovi: (C1)16
Spol: 
|
 Postano: 19:23 ned, 17. 2. 2008 Naslov: Postano: 19:23 ned, 17. 2. 2008 Naslov: |
    |
|
|
Još nekaj da provjerim jel ok. A={(x,y)eR2: x²-1<y<1-x²}
f1(x,y)=x²-1-y , f1^-1 (<0,+∞>) otvoren, isto tak za f2 i presjek 2 otvorena skupa je otvoren->skup nije kompaktan ? A što je s povezanosti?
Još nekaj da provjerim jel ok. A={(x,y)eR2: x²-1<y<1-x²}
f1(x,y)=x²-1-y , f1^-1 (<0,+∞>) otvoren, isto tak za f2 i presjek 2 otvorena skupa je otvoren->skup nije kompaktan ? A što je s povezanosti?
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
 Postano: 19:28 ned, 17. 2. 2008 Naslov: Postano: 19:28 ned, 17. 2. 2008 Naslov: |
    |
|
|
[quote="Blah"]Još nekaj da provjerim jel ok. A={(x,y)eR2: x²-1<y<1-x²}
f1(x,y)=x²-1-y , f1^-1 (<0,+∞>) otvoren, isto tak za f2 i presjek 2 otvorena skupa je otvoren->skup nije kompaktan ? A što je s povezanosti?[/quote]
Sta nije f1(x,y)=x^2-1-y<0 i onda je f(x,y)e<-besk,0>, odnosno f1^-1(<-besk,0>).
Prica stoji, samo mi se interval cini krivi. :wink:
| Blah (napisa): | Još nekaj da provjerim jel ok. A={(x,y)eR2: x²-1<y<1-x²}
f1(x,y)=x²-1-y , f1^-1 (<0,+∞>) otvoren, isto tak za f2 i presjek 2 otvorena skupa je otvoren→skup nije kompaktan ? A što je s povezanosti? |
Sta nije f1(x,y)=x^2-1-y<0 i onda je f(x,y)e←besk,0>, odnosno f1^-1(←besk,0>).
Prica stoji, samo mi se interval cini krivi. 
_________________  |
|
| [Vrh] |
|
Blah
Forumaš(ica)

Pridružen/a: 11. 09. 2006. (18:07:56)
Postovi: (C1)16
Spol: 
|
|
| [Vrh] |
|
|














