| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
strac
Forumaš(ica)

Pridružen/a: 25. 06. 2007. (17:14:36)
Postovi: (3)16
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 20:19 ned, 8. 6. 2008 Naslov: Postano: 20:19 ned, 8. 6. 2008 Naslov: |
    |
|
|
[latex]H \leqslant G[/latex]. definirali smo: [latex]x \sim y \Leftrightarrow x^{-1}y \in H[/latex].
u ovom primjeru, [latex]G = M_2( \mathbb{Z})[/latex] , a H gornje/donje trokutaste matrice s cjelobrojnim elementima. dakle, tu će u istoj klasi biti matrice koje imaju jednak broj na mjestu (2,1), odnosno (1,2). :wink:
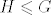 . definirali smo: . definirali smo: 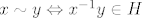 . .
u ovom primjeru, 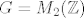 , a H gornje/donje trokutaste matrice s cjelobrojnim elementima. dakle, tu će u istoj klasi biti matrice koje imaju jednak broj na mjestu (2,1), odnosno (1,2). , a H gornje/donje trokutaste matrice s cjelobrojnim elementima. dakle, tu će u istoj klasi biti matrice koje imaju jednak broj na mjestu (2,1), odnosno (1,2). 
_________________
ima let u finish
|
|
| [Vrh] |
|
Nori
Forumaš(ica)
Pridružen/a: 01. 10. 2006. (18:41:07)
Postovi: (E5)16
Spol: 
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 7:29 pon, 9. 6. 2008 Naslov: Postano: 7:29 pon, 9. 6. 2008 Naslov: |
    |
|
|
[quote="ma"]
2. [latex]\mathbb{T} := \{ z \in \mathbb{C} : |z| = 1\}[/latex]. Definirali su homomorfizam (ne treba dokazati da je homomorfizam) [latex]f : \mathbb{R} \rightarrow \mathbb{T}[/latex] s [latex]f(x) = \cos x + i \sin x[/latex]. odredite jezgru i sliku. je li f mono, epi, izo? primijenite 1. tm o izomorfizmu :?
[/quote]
Jel tu dosta reć Kerf=Z*pi, Imf=T, pa je R/Zpi izomorfno sa T ?
I kako egzaktno dokazat da je epi? Jel dosta reć da uzmemo z iz T, pa onda za njega vrijedi da je na kružnici radijusa 1 oko nule, pa za svaku prvu koordinatu postoji druga t.d. vrijedi jedn. kružnice? :?
3.zad: nije int domena. Kontraprimjer ko i za 'obične' matrice. A za ideal se množenje matrica radi puta_modulo_4 ili obično?
| ma (napisa): |
2. 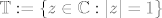 . Definirali su homomorfizam (ne treba dokazati da je homomorfizam) . Definirali su homomorfizam (ne treba dokazati da je homomorfizam) 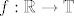 s s 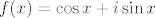 . odredite jezgru i sliku. je li f mono, epi, izo? primijenite 1. tm o izomorfizmu . odredite jezgru i sliku. je li f mono, epi, izo? primijenite 1. tm o izomorfizmu 
|
Jel tu dosta reć Kerf=Z*pi, Imf=T, pa je R/Zpi izomorfno sa T ?
I kako egzaktno dokazat da je epi? Jel dosta reć da uzmemo z iz T, pa onda za njega vrijedi da je na kružnici radijusa 1 oko nule, pa za svaku prvu koordinatu postoji druga t.d. vrijedi jedn. kružnice? 
3.zad: nije int domena. Kontraprimjer ko i za 'obične' matrice. A za ideal se množenje matrica radi puta_modulo_4 ili obično?
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 9:24 pon, 9. 6. 2008 Naslov: Postano: 9:24 pon, 9. 6. 2008 Naslov: |
    |
|
|
[quote="Luuka"]Jel tu dosta reć Kerf=Z*pi, Imf=T, pa je R/Zpi izomorfno sa T ?[/quote]
joj. ja sam dobio da je [latex]\text{Ker} f = 2 \pi \mathbb{Z}[/latex] :wall:
a ovaj drugi dio ti ne znam reć jer nažalost ne znam niti iskazati dotični teorem (više) :?
[quote="Luuka"]I kako egzaktno dokazat da je epi? Jel dosta reć da uzmemo z iz T, pa onda za njega vrijedi da je na kružnici radijusa 1 oko nule, pa za svaku prvu koordinatu postoji druga t.d. vrijedi jedn. kružnice? :?[/quote]
e vidiš- ne znam :D tu sam nešto prtljao, više se ni ne sjećam što sam točno pisao. ali mislim da je ovo tvoje donekle dobro. kompleksni brojevi modula 1 leže na toj jediničnoj kružnici, pa za svaki možemo naći prebrojivo mnogo realnih brojeva koji se preslikaju u njega :?
[quote="Luuka"]3.zad: nije int domena. Kontraprimjer ko i za 'obične' matrice. A za ideal se množenje matrica radi puta_modulo_4 ili obično?[/quote]
pa kaj ne bi općenito trebalo obavljati operaciju iz prstena. ovdje obično množenje. sad sam zbunjen. :bunny:
| Luuka (napisa): | | Jel tu dosta reć Kerf=Z*pi, Imf=T, pa je R/Zpi izomorfno sa T ? |
joj. ja sam dobio da je 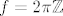 
a ovaj drugi dio ti ne znam reć jer nažalost ne znam niti iskazati dotični teorem (više) 
| Luuka (napisa): | I kako egzaktno dokazat da je epi? Jel dosta reć da uzmemo z iz T, pa onda za njega vrijedi da je na kružnici radijusa 1 oko nule, pa za svaku prvu koordinatu postoji druga t.d. vrijedi jedn. kružnice?  |
e vidiš- ne znam  tu sam nešto prtljao, više se ni ne sjećam što sam točno pisao. ali mislim da je ovo tvoje donekle dobro. kompleksni brojevi modula 1 leže na toj jediničnoj kružnici, pa za svaki možemo naći prebrojivo mnogo realnih brojeva koji se preslikaju u njega tu sam nešto prtljao, više se ni ne sjećam što sam točno pisao. ali mislim da je ovo tvoje donekle dobro. kompleksni brojevi modula 1 leže na toj jediničnoj kružnici, pa za svaki možemo naći prebrojivo mnogo realnih brojeva koji se preslikaju u njega 
| Luuka (napisa): | | 3.zad: nije int domena. Kontraprimjer ko i za 'obične' matrice. A za ideal se množenje matrica radi puta_modulo_4 ili obično? |
pa kaj ne bi općenito trebalo obavljati operaciju iz prstena. ovdje obično množenje. sad sam zbunjen. 
_________________
ima let u finish
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 9:42 pon, 9. 6. 2008 Naslov: Postano: 9:42 pon, 9. 6. 2008 Naslov: |
    |
|
|
Ako je normalno množenje, mislim da nije ideal. Uzmemo matricu iz tog potprstena (bilo koju) i neku iz cijelog prstena sa velikim brojevima... u matrici umnoška će opet bit veliki brojevi, a ne samo {0,1,2,3} 8)
Ako je normalno množenje, mislim da nije ideal. Uzmemo matricu iz tog potprstena (bilo koju) i neku iz cijelog prstena sa velikim brojevima... u matrici umnoška će opet bit veliki brojevi, a ne samo {0,1,2,3} 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 9:53 pon, 9. 6. 2008 Naslov: Postano: 9:53 pon, 9. 6. 2008 Naslov: |
    |
|
|
[quote="Luuka"]Ako je normalno množenje, mislim da nije ideal. Uzmemo matricu iz tog potprstena (bilo koju) i neku iz cijelog prstena sa velikim brojevima... u matrici umnoška će opet bit veliki brojevi, a ne samo {0,1,2,3} 8)[/quote]
hmda :? uglavnom, bunilo me ono- koju operaciju uzeti. tu se zapravo radi o matricama, pa je množenje matrica operacija iz prstena. a kako množiti elemente stvarno ne znam. rekao bih normalno- jer tako množimo matrice. zašto bi netko trebao pretpostaviti da elemente matrice treba množiti i zbrajati modulo 4 :?
dakle, po tvojoj napomeni- to nije ideal u R :wink:
| Luuka (napisa): | Ako je normalno množenje, mislim da nije ideal. Uzmemo matricu iz tog potprstena (bilo koju) i neku iz cijelog prstena sa velikim brojevima... u matrici umnoška će opet bit veliki brojevi, a ne samo {0,1,2,3}  |
hmda  uglavnom, bunilo me ono- koju operaciju uzeti. tu se zapravo radi o matricama, pa je množenje matrica operacija iz prstena. a kako množiti elemente stvarno ne znam. rekao bih normalno- jer tako množimo matrice. zašto bi netko trebao pretpostaviti da elemente matrice treba množiti i zbrajati modulo 4 uglavnom, bunilo me ono- koju operaciju uzeti. tu se zapravo radi o matricama, pa je množenje matrica operacija iz prstena. a kako množiti elemente stvarno ne znam. rekao bih normalno- jer tako množimo matrice. zašto bi netko trebao pretpostaviti da elemente matrice treba množiti i zbrajati modulo 4 
dakle, po tvojoj napomeni- to nije ideal u R 
_________________
ima let u finish
|
|
| [Vrh] |
|
Nori
Forumaš(ica)
Pridružen/a: 01. 10. 2006. (18:41:07)
Postovi: (E5)16
Spol: 
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
|















