|
U pravu si, da. Prvo trebaš izračunati (makar se to u pravilu samo nametne tijekom računanja slike, ali bolje je biti precizan pa to izračunati na početku) domenu cijele funkcije i onda tražiti sliku na tom skupu.
Na primjer, pogledajmo funkciju [latex]f(x)=\frac{1}{x-1}[/latex]. Prirodno, to rastavljamo na kompoziciju [latex]f_1(x)=\frac{1}{x}[/latex] i [latex]f_2(x)=x-1[/latex]. Vrijedi, dakako, [latex]f=f_1\circ f_2[/latex]. E, sad, domena od [latex]f_2[/latex] jest cijeli [latex]\mathbb{R}[/latex], tako da s te strane nemamo problema, ali ipak ne možemo dopustiti [latex]1[/latex] u domeni kad gledamo [latex]\mathcal{R}_f[/latex]. Naime, kad bismo gledali [latex]f_1(f_2(\mathbb{R}))[/latex], dobili bismo da je to jednako [latex]f_1(\mathbb{R})[/latex], a to nije baš sasvim točno (makar je jasno što mi hoćemo, ali svejedno nije najtočnije) budući da [latex]f_1[/latex] nije definirana u [latex]0[/latex].
U vezi zadatka 4. b), uzeo sam grupu A. Dakle, priča je jako slična a) dijelu, samo što su zaključci malo drugačiji.
Dakle, uzeo si [latex]f(x)[/latex] kao kompoziciju [latex]f_1(x)=x+1[/latex], [latex]f_2(x)=x^3[/latex] i [latex]f_3(x)=\sin x[/latex] (ili neka verzija toga, meni je jednostavnije razmišljati s najelementarnijim funkcijama). Sad, funkcija [latex]\sin x[/latex] je injektivna na svojoj domeni u ovom zadatku. Funkcije [latex]x+1[/latex] i [latex]x^3[/latex] su također injektivne na cijelom [latex]\mathbb{R}[/latex], pa specijalno i na intervalima koji nas zanimaju. Kao rezultat, [latex]f[/latex] je kompozicija injekcija, pa je i sama injekcija.
Inverznu funkciju najlakše je odrediti putem formule za inverznu funkciju kompozicije. Imamo, dakle, [latex]f^{-1}(x)=f_3^{-1}(f_2^{-1}(f_1^{-1}(x)))[/latex]. Znamo da je [latex]f_1^{-1}(x)=x-1[/latex], a [latex]f_2^{-1}(x)=\sqrt[3]{x}[/latex].
Još ostaje pitanje sinusa. Tu ne možemo samo iskoristiti arkus sinusa jer je njegova slika [latex][-\frac{\pi}{2},\frac{\pi}{2}][/latex]. No, primijetimo da je [latex]\sin x=\sin (x-2\pi)[/latex], pa će nam odgovarati da kao traženi inverz funkcije [latex]f_3[/latex] uzmemo [latex]\arcsin (x)+2\pi[/latex]. Tako ćemo dobiti prave vrijednosti jer smo osigurali "pomak" za [latex]2\pi[/latex]. Dakle, ako se ne varam, dobivamo da je [latex]f^{-1}(x)=\arcsin (\sqrt[3]{x-1})+2\pi[/latex]. To možemo i provjeriti.
Ovaj dio sa sinusom malo je zakučast, pa reci ako ima kakvih problema :). Osim toga bi zadatak trebao biti dosta lagan.
U pravu si, da. Prvo trebaš izračunati (makar se to u pravilu samo nametne tijekom računanja slike, ali bolje je biti precizan pa to izračunati na početku) domenu cijele funkcije i onda tražiti sliku na tom skupu.
Na primjer, pogledajmo funkciju 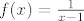 . Prirodno, to rastavljamo na kompoziciju . Prirodno, to rastavljamo na kompoziciju 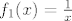 i i 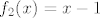 . Vrijedi, dakako, . Vrijedi, dakako, 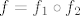 . E, sad, domena od . E, sad, domena od 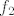 jest cijeli jest cijeli  , tako da s te strane nemamo problema, ali ipak ne možemo dopustiti , tako da s te strane nemamo problema, ali ipak ne možemo dopustiti  u domeni kad gledamo u domeni kad gledamo 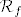 . Naime, kad bismo gledali . Naime, kad bismo gledali 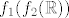 , dobili bismo da je to jednako , dobili bismo da je to jednako 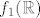 , a to nije baš sasvim točno (makar je jasno što mi hoćemo, ali svejedno nije najtočnije) budući da , a to nije baš sasvim točno (makar je jasno što mi hoćemo, ali svejedno nije najtočnije) budući da 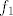 nije definirana u nije definirana u  . .
U vezi zadatka 4. b), uzeo sam grupu A. Dakle, priča je jako slična a) dijelu, samo što su zaključci malo drugačiji.
Dakle, uzeo si 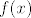 kao kompoziciju kao kompoziciju 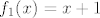 , , 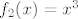 i i 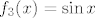 (ili neka verzija toga, meni je jednostavnije razmišljati s najelementarnijim funkcijama). Sad, funkcija (ili neka verzija toga, meni je jednostavnije razmišljati s najelementarnijim funkcijama). Sad, funkcija 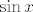 je injektivna na svojoj domeni u ovom zadatku. Funkcije je injektivna na svojoj domeni u ovom zadatku. Funkcije 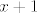 i i 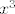 su također injektivne na cijelom su također injektivne na cijelom  , pa specijalno i na intervalima koji nas zanimaju. Kao rezultat, , pa specijalno i na intervalima koji nas zanimaju. Kao rezultat,  je kompozicija injekcija, pa je i sama injekcija. je kompozicija injekcija, pa je i sama injekcija.
Inverznu funkciju najlakše je odrediti putem formule za inverznu funkciju kompozicije. Imamo, dakle, 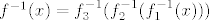 . Znamo da je . Znamo da je 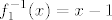 , a , a 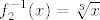 . .
Još ostaje pitanje sinusa. Tu ne možemo samo iskoristiti arkus sinusa jer je njegova slika 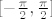 . No, primijetimo da je . No, primijetimo da je 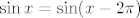 , pa će nam odgovarati da kao traženi inverz funkcije , pa će nam odgovarati da kao traženi inverz funkcije 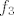 uzmemo uzmemo 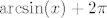 . Tako ćemo dobiti prave vrijednosti jer smo osigurali "pomak" za . Tako ćemo dobiti prave vrijednosti jer smo osigurali "pomak" za 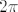 . Dakle, ako se ne varam, dobivamo da je . Dakle, ako se ne varam, dobivamo da je 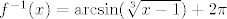 . To možemo i provjeriti. . To možemo i provjeriti.
Ovaj dio sa sinusom malo je zakučast, pa reci ako ima kakvih problema  . Osim toga bi zadatak trebao biti dosta lagan. . Osim toga bi zadatak trebao biti dosta lagan.
|





