| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 12:32 sri, 18. 11. 2009 Naslov: Postano: 12:32 sri, 18. 11. 2009 Naslov: |
    |
|
|
prikažeš polinom p u bazi B:
[latex]3x^3-4x^2+2x-5 = \alpha_1 (x-3)^3 + \alpha_2 (x-1)^2 + \alpha_3 (x-1) + \alpha_4[/latex]
Nakon raspisivanja desne strane (potenciranja), izjednačit koeficijente na lijevoj i desnoj strani, i tako dobijemo alfe, koji nam daju prikaz u bazi B.
Preko matrice prijelaza:
napravait matricu prijelaza iz kanonske baze u bazu B, i onda izmnožit matricu prijelaza sa vektorom (3,-4,2,-5) da se dobiju koeficijenti u bazi B.
(p.s. Ne sjećam se točno, moguće da treba tu matricu prijelaza invertirat pa onda množit s onim vektorom, nek to raspiše netko tko to sad radi :D )
prikažeš polinom p u bazi B:
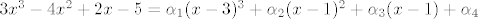
Nakon raspisivanja desne strane (potenciranja), izjednačit koeficijente na lijevoj i desnoj strani, i tako dobijemo alfe, koji nam daju prikaz u bazi B.
Preko matrice prijelaza:
napravait matricu prijelaza iz kanonske baze u bazu B, i onda izmnožit matricu prijelaza sa vektorom (3,-4,2,-5) da se dobiju koeficijenti u bazi B.
(p.s. Ne sjećam se točno, moguće da treba tu matricu prijelaza invertirat pa onda množit s onim vektorom, nek to raspiše netko tko to sad radi  ) )
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
 Postano: 17:35 sri, 18. 11. 2009 Naslov: Postano: 17:35 sri, 18. 11. 2009 Naslov: |
    |
|
|
[quote="Luuka"]prikažeš polinom p u bazi B:
[latex]3x^3-4x^2+2x-5 = \alpha_1 (x-3)^3 + \alpha_2 (x-1)^2 + \alpha_3 (x-1) + \alpha_4[/latex]
Nakon raspisivanja desne strane (potenciranja), izjednačit koeficijente na lijevoj i desnoj strani, i tako dobijemo alfe, koji nam daju prikaz u bazi B.
Preko matrice prijelaza:
napravait matricu prijelaza iz kanonske baze u bazu B, i onda izmnožit matricu prijelaza sa vektorom (3,-4,2,-5) da se dobiju koeficijenti u bazi B.
(p.s. Ne sjećam se točno, moguće da treba tu matricu prijelaza invertirat pa onda množit s onim vektorom, nek to raspiše netko tko to sad radi :D )[/quote]
[size=9][color=#999999]Added after 53 seconds:[/color][/size]
Iii, jel tko upoznat s ovim gradivom?
[size=9][color=#999999]Added after 1 minutes:[/color][/size]
Evo, to matematičari uvide, razliku kavadrata i sl.
Ja zaboravim na to i nema šanse da bi se sam sjetio...
Eh..
| Luuka (napisa): | prikažeš polinom p u bazi B:
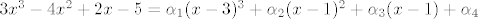
Nakon raspisivanja desne strane (potenciranja), izjednačit koeficijente na lijevoj i desnoj strani, i tako dobijemo alfe, koji nam daju prikaz u bazi B.
Preko matrice prijelaza:
napravait matricu prijelaza iz kanonske baze u bazu B, i onda izmnožit matricu prijelaza sa vektorom (3,-4,2,-5) da se dobiju koeficijenti u bazi B.
(p.s. Ne sjećam se točno, moguće da treba tu matricu prijelaza invertirat pa onda množit s onim vektorom, nek to raspiše netko tko to sad radi  ) ) |
Added after 53 seconds:
Iii, jel tko upoznat s ovim gradivom?
Added after 1 minutes:
Evo, to matematičari uvide, razliku kavadrata i sl.
Ja zaboravim na to i nema šanse da bi se sam sjetio...
Eh..
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 23:07 sri, 18. 11. 2009 Naslov: Postano: 23:07 sri, 18. 11. 2009 Naslov: |
    |
|
|
sve bez x-eva... samo koeficijente izjednačuješ, x-ovi se onda izgube iz priče.
A sustav riješiš npr:
iz prve slijedi da je alfa1=3.
onda iz druge dobiješ alfa2 (jer znaš alfa1), pa iz treće alfa3(jer znaš alfa1 i alfa2), pa iz četvrte alfa4.
I to je to. Dobio si alfe, pa imaš prikaz u bazi B.
sve bez x-eva... samo koeficijente izjednačuješ, x-ovi se onda izgube iz priče.
A sustav riješiš npr:
iz prve slijedi da je alfa1=3.
onda iz druge dobiješ alfa2 (jer znaš alfa1), pa iz treće alfa3(jer znaš alfa1 i alfa2), pa iz četvrte alfa4.
I to je to. Dobio si alfe, pa imaš prikaz u bazi B.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
tomi365
Forumaš(ica)

Pridružen/a: 17. 11. 2009. (18:07:47)
Postovi: (25)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|













