| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 19:40 uto, 19. 1. 2010 Naslov: Re: 4.zadaća Postano: 19:40 uto, 19. 1. 2010 Naslov: Re: 4.zadaća |
    |
|
|
[quote="A_je_to"]http://web.math.hr/nastava/la/zadace/la1_09-10/dz4.pdf
Molio bi da mi netko objasni 3. zadatak. Hvala![/quote]
Ako su [latex]b_i[/latex]retci matrice B, uoci da je i-ti redak matrice AB jednak [latex]a_{i,1} b_1 + \ldots + a_{i, n} b_n[/latex], pa je svaki redak matrice AB linearna kombinacija redaka matrice B, odakle slijedi da je [latex]r(AB) \leq r(B) (*)[/latex](ne mozes "izmisliti" nove, nezavisne retke pomocu linearne kombinacije).
rang transponirane matrice je jednak rangu originalne, pa je [latex]r(AB) = r((AB)^\tau) = r(B^\tau A^\tau)[/latex] a po vec pokazanom (*), to je manje od ranga druge matrice iz produkta, [latex]r(AB) \leq r(A^\tau) = r(A)[/latex] jer je rang transponirane matrice jednag rangu originalne
| A_je_to (napisa): | http://web.math.hr/nastava/la/zadace/la1_09-10/dz4.pdf
Molio bi da mi netko objasni 3. zadatak. Hvala! |
Ako su 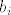 retci matrice B, uoci da je i-ti redak matrice AB jednak retci matrice B, uoci da je i-ti redak matrice AB jednak  , pa je svaki redak matrice AB linearna kombinacija redaka matrice B, odakle slijedi da je , pa je svaki redak matrice AB linearna kombinacija redaka matrice B, odakle slijedi da je 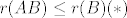 (ne mozes "izmisliti" nove, nezavisne retke pomocu linearne kombinacije). (ne mozes "izmisliti" nove, nezavisne retke pomocu linearne kombinacije).
rang transponirane matrice je jednak rangu originalne, pa je 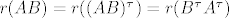 a po vec pokazanom (*), to je manje od ranga druge matrice iz produkta, a po vec pokazanom (*), to je manje od ranga druge matrice iz produkta, 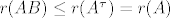 jer je rang transponirane matrice jednag rangu originalne jer je rang transponirane matrice jednag rangu originalne
_________________
Bri
|
|
| [Vrh] |
|
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
 Postano: 10:52 sri, 20. 1. 2010 Naslov: Postano: 10:52 sri, 20. 1. 2010 Naslov: |
    |
|
|
[quote="pmli"]Za takve stavri dobro dođe [url=http://www.wolframalpha.com/]Wolfram Alpha[/url]. Utipkaj Inverse[{{2,1,2},{1,2,2},{3,3,3}}].[/quote]
Kako za determinante n-tog reda? Pokušala sam s raznim inačicama trotočja pa nije prepoznalo uzorak, valjda loša sintaksa :?
| pmli (napisa): | | Za takve stavri dobro dođe Wolfram Alpha. Utipkaj Inverse[{{2,1,2},{1,2,2},{3,3,3}}]. |
Kako za determinante n-tog reda? Pokušala sam s raznim inačicama trotočja pa nije prepoznalo uzorak, valjda loša sintaksa 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
c4rimson
Forumaš(ica)

Pridružen/a: 11. 01. 2010. (18:57:26)
Postovi: (3B)16
|
 Postano: 16:11 sri, 20. 1. 2010 Naslov: Postano: 16:11 sri, 20. 1. 2010 Naslov: |
    |
|
|
[quote="pmli"]Što ako je [latex]\lambda=-2[/latex]?
Opet, provjeri u Wolfram Alphi (MatrixRank[{{1,4,3,-2},{2,2,1,7},{4,1,-2,4},{-1,5,6,1}}]). [size=4]Trebali bi mi platiti koliko reklamiram njihov proizvod[/size][/quote]
kako si dobio da je [latex]\lambda=-2[/latex]?
| pmli (napisa): | Što ako je 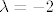 ? ?
Opet, provjeri u Wolfram Alphi (MatrixRank[{{1,4,3,-2},{2,2,1,7},{4,1,-2,4},{-1,5,6,1}}]). Trebali bi mi platiti koliko reklamiram njihov proizvod |
kako si dobio da je 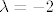 ? ?
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
c4rimson
Forumaš(ica)

Pridružen/a: 11. 01. 2010. (18:57:26)
Postovi: (3B)16
|
 Postano: 17:25 sri, 20. 1. 2010 Naslov: Postano: 17:25 sri, 20. 1. 2010 Naslov: |
    |
|
|
Ja sam dobio matricu {1,4,3,-2},{0,-6,-5,11},{0,-15,-12-A,12},{0,9,9,-1}. Kako se iz ovoga moze zakljuciti da je treci redak visekratnik drugog ili treceg retka?
Ja sam dobio matricu {1,4,3,-2},{0,-6,-5,11},{0,-15,-12-A,12},{0,9,9,-1}. Kako se iz ovoga moze zakljuciti da je treci redak visekratnik drugog ili treceg retka?
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
 Postano: 17:30 sri, 20. 1. 2010 Naslov: Postano: 17:30 sri, 20. 1. 2010 Naslov: |
    |
|
|
[quote="c4rimson"]Ja sam dobio matricu {1,4,3,-2},{0,-6,-5,11},{0,-15,-12-A,12},{0,9,9,-1}. Kako se iz ovoga moze zakljuciti da je treci redak visekratnik drugog ili treceg retka?[/quote]
možda je linearna kombinacija preostalih redaka
trebaš još dalje rješavati
| c4rimson (napisa): | | Ja sam dobio matricu {1,4,3,-2},{0,-6,-5,11},{0,-15,-12-A,12},{0,9,9,-1}. Kako se iz ovoga moze zakljuciti da je treci redak visekratnik drugog ili treceg retka? |
možda je linearna kombinacija preostalih redaka
trebaš još dalje rješavati
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 19:34 sri, 20. 1. 2010 Naslov: Postano: 19:34 sri, 20. 1. 2010 Naslov: |
    |
|
|
kako je grga dobio partikularno rješenje u 5.zadatku? stranica prije ove.
nikako da shvatim..
ja sam dobila (0,0,-3,0),ako je to uopće dobro?
mislim na postupak je li dobar?
daljnjim el.tran. sam dobila matricu:
1 2 0 1
0 0 1 3
0 0 0 0
0 0 0 0
i od tuda sam dobila da je x=(-2s-t,s,-3-3t,t) i odavde dobim da je x=(0,0,-3,0)+s(-2,1,0,0)+t(-1,0,-3,1)
kako je grga dobio partikularno rješenje u 5.zadatku? stranica prije ove.
nikako da shvatim..
ja sam dobila (0,0,-3,0),ako je to uopće dobro?
mislim na postupak je li dobar?
daljnjim el.tran. sam dobila matricu:
1 2 0 1
0 0 1 3
0 0 0 0
0 0 0 0
i od tuda sam dobila da je x=(-2s-t,s,-3-3t,t) i odavde dobim da je x=(0,0,-3,0)+s(-2,1,0,0)+t(-1,0,-3,1)
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
 Postano: 20:17 sri, 20. 1. 2010 Naslov: Re: 4.zadaća Postano: 20:17 sri, 20. 1. 2010 Naslov: Re: 4.zadaća |
    |
|
|
[quote="Grga"]
Ako su [latex]b_i[/latex]retci matrice B, uoci da je i-ti redak matrice AB jednak [latex]a_{i,1} b_1 + \ldots + a_{i, n} b_n[/latex], pa je svaki redak matrice AB linearna kombinacija redaka matrice B, odakle slijedi da je [latex]r(AB) \leq r(B) (*)[/latex](ne mozes "izmisliti" nove, nezavisne retke pomocu linearne kombinacije).[/quote]
moze li mi netko to pojasnit ili napisat neku drugu ideju dokaza
| Grga (napisa): |
Ako su 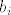 retci matrice B, uoci da je i-ti redak matrice AB jednak retci matrice B, uoci da je i-ti redak matrice AB jednak  , pa je svaki redak matrice AB linearna kombinacija redaka matrice B, odakle slijedi da je , pa je svaki redak matrice AB linearna kombinacija redaka matrice B, odakle slijedi da je 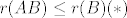 (ne mozes "izmisliti" nove, nezavisne retke pomocu linearne kombinacije). (ne mozes "izmisliti" nove, nezavisne retke pomocu linearne kombinacije). |
moze li mi netko to pojasnit ili napisat neku drugu ideju dokaza
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
 Postano: 20:34 sri, 20. 1. 2010 Naslov: Postano: 20:34 sri, 20. 1. 2010 Naslov: |
    |
|
|
[quote=".anchy."]kako je grga dobio partikularno rješenje u 5.zadatku? stranica prije ove.
nikako da shvatim..
ja sam dobila (0,0,-3,0),ako je to uopće dobro?
mislim na postupak je li dobar?
daljnjim el.tran. sam dobila matricu:
1 2 0 1
0 0 1 3
0 0 0 0
0 0 0 0
i od tuda sam dobila da je x=(-2s-t,s,-3-3t,t) i odavde dobim da je x=(0,0,-3,0)+s(-2,1,0,0)+t(-1,0,-3,1)[/quote]
ja sam prvo uzeo razliku 4. i 1. stupca (0,3,3,0) pa sam dobio drugo rješenje
ali inače i ja sam dobio tako :P
| .anchy. (napisa): | kako je grga dobio partikularno rješenje u 5.zadatku? stranica prije ove.
nikako da shvatim..
ja sam dobila (0,0,-3,0),ako je to uopće dobro?
mislim na postupak je li dobar?
daljnjim el.tran. sam dobila matricu:
1 2 0 1
0 0 1 3
0 0 0 0
0 0 0 0
i od tuda sam dobila da je x=(-2s-t,s,-3-3t,t) i odavde dobim da je x=(0,0,-3,0)+s(-2,1,0,0)+t(-1,0,-3,1) |
ja sam prvo uzeo razliku 4. i 1. stupca (0,3,3,0) pa sam dobio drugo rješenje
ali inače i ja sam dobio tako 
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 21:14 sri, 20. 1. 2010 Naslov: Re: 4.zadaća Postano: 21:14 sri, 20. 1. 2010 Naslov: Re: 4.zadaća |
    |
|
|
[quote=".anchy."]ummm..ne kužim.. :D
ako su stupci matrice 4x1, i x je 4x1 kako da ih pomnožim?mislim,očito sam krivo shvatila..al neznam kako drugačije..[/quote]
matrica x je 4x1, ali je x_i skalar, odnosno realan broj. Matrica A je 4x4 ali je a_i stupac, tj 4x1.
[size=9][color=#999999]Added after 5 minutes:[/color][/size]
Primijeti da su rjesenja ista, samo je partikularno rjesenje razlicito, ali su u istoj linearnoj mnogostrukosti (tj. dodavanjem linearne kombinacije vektora iz skupa fundamentalnih rjesenja mojem partikularnom rjesenju mozes dobit tvoje i obratno - konkretno uzmes t = 0 i s = -1 i dobijes moje partikularno rjesenje)
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
[quote="eve"][quote="Grga"]
Ako su [latex]b_i[/latex]retci matrice B, uoci da je i-ti redak matrice AB jednak [latex]a_{i,1} b_1 + \ldots + a_{i, n} b_n[/latex], pa je svaki redak matrice AB linearna kombinacija redaka matrice B, odakle slijedi da je [latex]r(AB) \leq r(B) (*)[/latex](ne mozes "izmisliti" nove, nezavisne retke pomocu linearne kombinacije).[/quote]
moze li mi netko to pojasnit ili napisat neku drugu ideju dokaza[/quote]
Koji dio ti nije jasan? Ako ti nije jasno zasto vrijedi da su retci od AB linearna kombinacija redaka od B, procitaj sto sam napisao pa probaj malo sama izmnoziti neke dvije matrice, pa ces valjda skuziti (mene je isto u pocetku dosta bilo mucilo uocavanje takvih stvari).
Iz nekog skupa vektora sigurno ne mozes linearnim kombinacijama dobiti vise linearno nezaviznih vektora nego sto ih na pocetku imas, a s obzirom da su retci od AB lienarna kombinacija redaka od B, onda imas najvise jednako linearno nezavisnih redaka kao u B
| .anchy. (napisa): | ummm..ne kužim.. 
ako su stupci matrice 4x1, i x je 4x1 kako da ih pomnožim?mislim,očito sam krivo shvatila..al neznam kako drugačije.. |
matrica x je 4x1, ali je x_i skalar, odnosno realan broj. Matrica A je 4x4 ali je a_i stupac, tj 4x1.
Added after 5 minutes:
Primijeti da su rjesenja ista, samo je partikularno rjesenje razlicito, ali su u istoj linearnoj mnogostrukosti (tj. dodavanjem linearne kombinacije vektora iz skupa fundamentalnih rjesenja mojem partikularnom rjesenju mozes dobit tvoje i obratno - konkretno uzmes t = 0 i s = -1 i dobijes moje partikularno rjesenje)
Added after 2 minutes:
| eve (napisa): | | Grga (napisa): |
Ako su 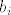 retci matrice B, uoci da je i-ti redak matrice AB jednak retci matrice B, uoci da je i-ti redak matrice AB jednak  , pa je svaki redak matrice AB linearna kombinacija redaka matrice B, odakle slijedi da je , pa je svaki redak matrice AB linearna kombinacija redaka matrice B, odakle slijedi da je 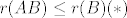 (ne mozes "izmisliti" nove, nezavisne retke pomocu linearne kombinacije). (ne mozes "izmisliti" nove, nezavisne retke pomocu linearne kombinacije). |
moze li mi netko to pojasnit ili napisat neku drugu ideju dokaza |
Koji dio ti nije jasan? Ako ti nije jasno zasto vrijedi da su retci od AB linearna kombinacija redaka od B, procitaj sto sam napisao pa probaj malo sama izmnoziti neke dvije matrice, pa ces valjda skuziti (mene je isto u pocetku dosta bilo mucilo uocavanje takvih stvari).
Iz nekog skupa vektora sigurno ne mozes linearnim kombinacijama dobiti vise linearno nezaviznih vektora nego sto ih na pocetku imas, a s obzirom da su retci od AB lienarna kombinacija redaka od B, onda imas najvise jednako linearno nezavisnih redaka kao u B
_________________
Bri
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
|

















