| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
andra
Forumaš(ica)

Pridružen/a: 02. 11. 2009. (19:23:23)
Postovi: (4F)16
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 19:00 uto, 12. 1. 2010 Naslov: Postano: 19:00 uto, 12. 1. 2010 Naslov: |
    |
|
|
Znači zadatak pretpostavljam glasi:
Odredite koeficijent [latex] a \in \mathbb{R} [/latex] tako da nultočke polinoma [latex]f(x)=x^{3}-\frac{3}{2}x^{2}+ax+1[/latex] zadovoljavaju jednakost [latex]x_{1}^{2}+x_{2}^{2}+x_{3}^{2}= \frac{21}{4}.[/latex] Odredite koje su to nultočke.
Najbitnije je u zadatku uočiti primjenu Vietovih formula.
Dakle [latex]x_{1}^{2}+x_{2}^{2}+x_{3}^{2}[/latex] se moze zapisati kao [latex](x_{1}+x_{2}+x_{3})^{2}-2(x_{1}x_{2}+x_{2}x_{3}+x_{1}x_{3})[/latex].
Ovo prepoznaš kao Vietove formule, te primijetiš da je
[latex]x_{1}+x_{2}+x_{3}=\frac{3}{2}[/latex] i
[latex]x_{1}x_{2}+x_{2}x_{3}+x_{1}x_{3}=a[/latex].
Iz potonjeg dobijemo jednadžbu:
[latex](\frac{3}{2})^{2}-2\cdot a=\frac{21}{4}[/latex], iz čega slijedi da je [latex]a=-\frac{3}{2}[/latex]
Sada te trazi da nađeš nultočke, a to je sada lako, jer računaš nultočke od polinoma [latex]f(x)=x^{3}-\frac{3}{2}x^{2}-\frac{3}{2}x+1[/latex]
Možeš naći preko kandidata za cjelobrojne nultočke, pa kad nađeš jednu iskoristiš opet Vietove formule i nađeš preostale dvije.
Rješenja bi trebala biti -1, 2 i [latex]\frac{1}{2}[/latex].
Znači zadatak pretpostavljam glasi:
Odredite koeficijent 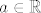 tako da nultočke polinoma tako da nultočke polinoma 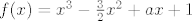 zadovoljavaju jednakost zadovoljavaju jednakost 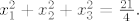 Odredite koje su to nultočke. Odredite koje su to nultočke.
Najbitnije je u zadatku uočiti primjenu Vietovih formula.
Dakle 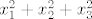 se moze zapisati kao se moze zapisati kao 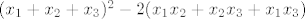 . .
Ovo prepoznaš kao Vietove formule, te primijetiš da je
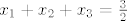 i i
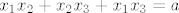 . .
Iz potonjeg dobijemo jednadžbu:
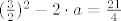 , iz čega slijedi da je , iz čega slijedi da je 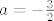
Sada te trazi da nađeš nultočke, a to je sada lako, jer računaš nultočke od polinoma 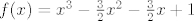
Možeš naći preko kandidata za cjelobrojne nultočke, pa kad nađeš jednu iskoristiš opet Vietove formule i nađeš preostale dvije.
Rješenja bi trebala biti -1, 2 i 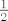 . .
|
|
| [Vrh] |
|
andra
Forumaš(ica)

Pridružen/a: 02. 11. 2009. (19:23:23)
Postovi: (4F)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 20:42 uto, 12. 1. 2010 Naslov: Postano: 20:42 uto, 12. 1. 2010 Naslov: |
    |
|
|
[quote="Genaro"]Dokažite da su svi realni polinomi trećeg stupnja reducibilni nad [latex]\mathbb{R}[/latex].
Molio bih ideju rješavanja, i jedno pitanje vezano uz zadatak: Ako kaže polinom reducibilan nad [latex]\mathbb{R}[/latex]., znači li to da su koeficijenti iz [latex]\mathbb{R}[/latex], nultočke, ili pak oboje?[/quote]
Definicija kaže da, ako je P komutativni prsten s jedinicom, f polinom iz P[x] (što znači da su mu koef. iz P) i postoje polinomi g i h također iz P[x] (svaki stupnja barem 1), te f(x)=g(x)h(x), kažemo da je f reducibilan (nad P).
U našem slučaju, imamo polinom trećeg stupnja s koef. iz R. Ne znamo kakve su mu nultočke, ali znamo da, ako je neki kompleksni broj nultočka, onda je i njegov konjugrani parnjak također nultočka.
Možeš li dalje sam?
[quote="ante c"]Jel se može 2 zad riješit ovako :
ako je f(p/q)=0
f(x)=(x-p/q)(x^(n-1)a(n)+x^(n-2)a(n-1)+..........+a1)
f(x)=x^na(n)+x^(n-1)a(n-1)+..........+xa1-p/q(x^(n-1))a(n)-p/q(x^(n-2))a(n-1)+................+(p/q)a1
sada iz zadatka znamo da je an element Z n{1,2,3...........} i p,q element Z.....................
onda imamo pitanje zapravo da li p|(p*a1)/q...............što je onda očito valjda istina :D[/quote]
Je. (p*a1)/q je cijeli broj, a kako su p i q rel. prosti, slijedi da q|a1. Sad je očito (p*a1)/q višekratnik od p, a time p|(p*a1)/q
[quote="eve"]Da li bi netko mogao na nekom primjeru objasnit kako se rjesavaju zadaci u kojima je potrebno odredit ostatak pri djeljenju dva broja (ili zbroja dva broja sa nekim trecim) kada ne vrijedi mali ferma[b]t[/b]ov teorem?[/quote]
Ako su brojevi dovoljno mali (manje od 10 znamenaka), iskoristiš kalkulator :D.
Tebe vjerojatno više zanimaju grdosije tipa [latex]8452986283^{429108757}[/latex], pri dijeljenju s, npr. [latex]10[/latex]. Ovdje ne možeš koristiti Mali Fermatov teorem jer 10 nije prost broj, ali postoji Eulerov teorem (koji je zapravo općenitija verzija Malog Fermata). On kaže da je [latex]a^{\varphi(m)}\equiv1(mod~m)[/latex], gdje su [latex]a, m \in \mathbb{N}, M(a,m)=1[/latex], a [latex]\varphi(m)[/latex] broj brojeva iz skupa [latex]\{1,\ldots,m\}[/latex] koji su rel. prosti s [latex]m[/latex] (Eulerova funkcija). Primjetimo da je [latex]8452986283\equiv3(mod~10)[/latex], pa je [latex]8452986283^{429108757}\equiv3^{429108757}(mod~10)[/latex]. Po Eulerovom tm. slijedi [latex]3^4\equiv1(mod~10)[/latex]. Vidimo da je [latex]429108757\equiv4291087\cdot100+57\equiv57\equiv1(mod~4)[/latex]. Napokon, [latex]3^4\equiv1(mod~10)[/latex] potenciramo odgovarajućim brojem da dobijemo [latex]3^{429108756}\equiv1(mod~10)[/latex], što pomnožimo s 3: [latex]3^{429108757}\equiv3(mod~10)[/latex]. Dakle, [latex]8452986283^{429108757}\equiv3(mod~10)[/latex].
Kod sumi gledaš svaki pribrojnik posebno na gornji način, pa na kraju zbrojiš.
| Genaro (napisa): | Dokažite da su svi realni polinomi trećeg stupnja reducibilni nad  . .
Molio bih ideju rješavanja, i jedno pitanje vezano uz zadatak: Ako kaže polinom reducibilan nad  ., znači li to da su koeficijenti iz ., znači li to da su koeficijenti iz  , nultočke, ili pak oboje? , nultočke, ili pak oboje? |
Definicija kaže da, ako je P komutativni prsten s jedinicom, f polinom iz P[x] (što znači da su mu koef. iz P) i postoje polinomi g i h također iz P[x] (svaki stupnja barem 1), te f(x)=g(x)h(x), kažemo da je f reducibilan (nad P).
U našem slučaju, imamo polinom trećeg stupnja s koef. iz R. Ne znamo kakve su mu nultočke, ali znamo da, ako je neki kompleksni broj nultočka, onda je i njegov konjugrani parnjak također nultočka.
Možeš li dalje sam?
| ante c (napisa): | Jel se može 2 zad riješit ovako :
ako je f(p/q)=0
f(x)=(x-p/q)(x^(n-1)a(n)+x^(n-2)a(n-1)+..........+a1)
f(x)=x^na(n)+x^(n-1)a(n-1)+..........+xa1-p/q(x^(n-1))a(n)-p/q(x^(n-2))a(n-1)+................+(p/q)a1
sada iz zadatka znamo da je an element Z n{1,2,3...........} i p,q element Z.....................
onda imamo pitanje zapravo da li p|(p*a1)/q...............što je onda očito valjda istina  |
Je. (p*a1)/q je cijeli broj, a kako su p i q rel. prosti, slijedi da q|a1. Sad je očito (p*a1)/q višekratnik od p, a time p|(p*a1)/q
| eve (napisa): | | Da li bi netko mogao na nekom primjeru objasnit kako se rjesavaju zadaci u kojima je potrebno odredit ostatak pri djeljenju dva broja (ili zbroja dva broja sa nekim trecim) kada ne vrijedi mali fermatov teorem? |
Ako su brojevi dovoljno mali (manje od 10 znamenaka), iskoristiš kalkulator  . .
Tebe vjerojatno više zanimaju grdosije tipa 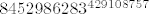 , pri dijeljenju s, npr. , pri dijeljenju s, npr.  . Ovdje ne možeš koristiti Mali Fermatov teorem jer 10 nije prost broj, ali postoji Eulerov teorem (koji je zapravo općenitija verzija Malog Fermata). On kaže da je . Ovdje ne možeš koristiti Mali Fermatov teorem jer 10 nije prost broj, ali postoji Eulerov teorem (koji je zapravo općenitija verzija Malog Fermata). On kaže da je 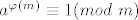 , gdje su , gdje su 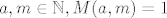 , a , a 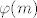 broj brojeva iz skupa broj brojeva iz skupa 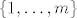 koji su rel. prosti s koji su rel. prosti s  (Eulerova funkcija). Primjetimo da je (Eulerova funkcija). Primjetimo da je 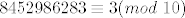 , pa je , pa je 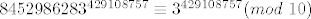 . Po Eulerovom tm. slijedi . Po Eulerovom tm. slijedi 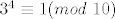 . Vidimo da je . Vidimo da je 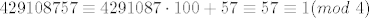 . Napokon, . Napokon, 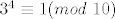 potenciramo odgovarajućim brojem da dobijemo potenciramo odgovarajućim brojem da dobijemo  , što pomnožimo s 3: , što pomnožimo s 3:  . Dakle, . Dakle, 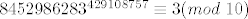 . .
Kod sumi gledaš svaki pribrojnik posebno na gornji način, pa na kraju zbrojiš.
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 0:16 sri, 13. 1. 2010 Naslov: Postano: 0:16 sri, 13. 1. 2010 Naslov: |
    |
|
|
[quote]3)Definirajte simetrični polinom u n varijabli , te te elementarne simetrične i Newtonovepolinome u n varijabli (OVAJ BAŠ NEZNAM RIJEŠIT Sad ); [/quote]
Mislim da smo ovo radili na predavanjima, ali evo, preuzeti ću definicije iz knjige Elementarna matematika 1 (Pavković-Veljan):
1. Za polinom [latex]f \in \mathbb{R}[x_{1},x_{2},...,x_{n}][/latex] kažemo da je [b]simetričan[/b] ako vrijedi
[latex]f(x_{1},x_{2},... ,x_{n})=f(x_{\pi(1)},x_{\pi(2)},...,x_{\pi (n)})[/latex]
za svaku permutaciju (bijekciju) [latex]\pi : \{1,2, ... , n\} \rightarrow \{1,2,...,n\}[/latex]
2. [b]Elementarne simetične polinome[/b] u n varijabli definiramo na sljedeći način:
[latex]\sigma_{1} = x_{1} + x_{2} + ... + x_{n}[/latex]
[latex]\sigma_{2} = x_{1}x_{2} + x_{2}x_{3} + ... + x_{n-1}x_{n}[/latex]
[latex]\sigma_{3} = x_{1}x_{2}x_{3} + x_{1}x_{2}x_{4} + ... + x_{n-2}x_{n-1}x_{n}[/latex]
.................................................................................
[latex]\sigma_{n} = x_{1} \cdot x_{2} \cdot ... \cdot x_{n}[/latex]
3. [b]Newtonove polinome[/b] ili sume potencija u n varijabli definiramo kao klasu simetričnih polinoma, i to na sljedeći način:
[latex]S_{1} = x_{1} + x_{2} + ... + x_{n}[/latex]
[latex]S_{2} = x_{1}^{2} + x_{2}^{2} + ... + x_{n}^{2}[/latex]
.............................................
[latex]S_{k} = x_{1}^{k} + x_{2}^{k} + ... + x_{n}^{k}[/latex]
Eto, nadam se da to odgovara na tvoje pitanje.
| Citat: | | 3)Definirajte simetrični polinom u n varijabli , te te elementarne simetrične i Newtonovepolinome u n varijabli (OVAJ BAŠ NEZNAM RIJEŠIT Sad ); |
Mislim da smo ovo radili na predavanjima, ali evo, preuzeti ću definicije iz knjige Elementarna matematika 1 (Pavković-Veljan):
1. Za polinom 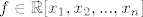 kažemo da je simetričan ako vrijedi kažemo da je simetričan ako vrijedi
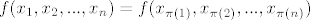
za svaku permutaciju (bijekciju) 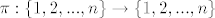
2. Elementarne simetične polinome u n varijabli definiramo na sljedeći način:
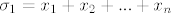
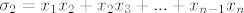
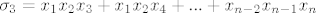
.................................................................................
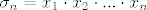
3. Newtonove polinome ili sume potencija u n varijabli definiramo kao klasu simetričnih polinoma, i to na sljedeći način:
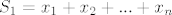
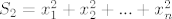
.............................................
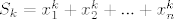
Eto, nadam se da to odgovara na tvoje pitanje.
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 12:25 sri, 13. 1. 2010 Naslov: Postano: 12:25 sri, 13. 1. 2010 Naslov: |
    |
|
|
[quote="medonja"]Pokažite da 3 ne dijeli n^3+n^2-n+1 za sve n element N. Hvala unaprijed.[/quote]
Neka je [latex]n\equiv k(mod~3)[/latex], gdje je [latex]k\in\{0,1,-1\}[/latex].
Slijedi da je [latex]n^3+n^2-n+1\equiv k^3+k^2-k+1~(mod~3)[/latex]. Dakle, imaš tri slučaja (ovisno o k). Uvrstiš i dobiš da je ostatak uvijek različit od 0.
[quote="medonja"]Odredite sve polinome p element R[x] takve da je p(2x)=2p(x), za svaki x element R.[/quote]
Ne možemo odrediti uvjet na stupanj polinoma p, pa uzmemo da je [latex]p(x)=a_nx^n+\ldots+a_0[/latex]. Uvrstiš u jednakost i zaključiš da svi koef. moraju biti nula, osim onog uz [latex]x[/latex], tj. [latex]a_1[/latex]. Stoga su rješenja svi linearni polinomi i nulpolinom.
| medonja (napisa): | | Pokažite da 3 ne dijeli n^3+n^2-n+1 za sve n element N. Hvala unaprijed. |
Neka je 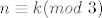 , gdje je , gdje je 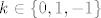 . .
Slijedi da je 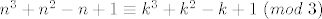 . Dakle, imaš tri slučaja (ovisno o k). Uvrstiš i dobiš da je ostatak uvijek različit od 0. . Dakle, imaš tri slučaja (ovisno o k). Uvrstiš i dobiš da je ostatak uvijek različit od 0.
| medonja (napisa): | | Odredite sve polinome p element R[x] takve da je p(2x)=2p(x), za svaki x element R. |
Ne možemo odrediti uvjet na stupanj polinoma p, pa uzmemo da je 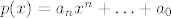 . Uvrstiš u jednakost i zaključiš da svi koef. moraju biti nula, osim onog uz . Uvrstiš u jednakost i zaključiš da svi koef. moraju biti nula, osim onog uz  , tj. , tj. 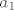 . Stoga su rješenja svi linearni polinomi i nulpolinom. . Stoga su rješenja svi linearni polinomi i nulpolinom.
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 18:07 sri, 13. 1. 2010 Naslov: Postano: 18:07 sri, 13. 1. 2010 Naslov: |
    |
|
|
[quote="meda"]imam pitanje za 7 zadatak iz prošlogodišnjeg kolokvija(1. grupa)...ugl meni ispada p(x)=x i p(x)=x^2, al mi je to nekak sumnjivo...jel neko možda rješavao taj zadatak?[/quote]
Pretpostavljam da misliš na zadatak s [latex]p(x^2)=(p(x))^2, \forall x \in \mathbb{R}, p\in\mathbb{R}[x],st~p\leq2[/latex]. Uzmeš da je [latex]p(x)=ax^2+bx+c[/latex], uvrstiš u jednakost, dobiš pet jednadžbi: [latex]a=a^2, 0=2ab, b=b^2+2ac, 0=2bc, c=c^2[/latex]. Ideš po slučajevima: 1° [latex]a=0 \ldots[/latex], 2° [latex]a=1\ldots[/latex]
Dobiju se kao rješenja uz tvoje [latex]p(x)\equiv0[/latex] i [latex]p(x)\equiv1[/latex].
[quote="Black Mamba"]Definirajte skup Z pomocu relacije ekvivalencije. Dokazite da je ta relacija doista relacija ekvivalencije.[/quote]
Ideja je da svaki cijeli broj možemo prikazati kao razliku dva prirodna. Nažalost, taj prikaz nije jedinstven. Stoga uvodimo relaciju kojom ćemo poistovijetiti neke razlike.
Promatramo skup [latex]\mathbb{N}\times\mathbb{N}[/latex]. Elementi tog skupa su parovi koje shvaćamo kao razlike: [latex](a,b)=a-b[/latex]. Zato kažemo da su dva para [latex](a,b)[/latex] i [latex](c,d)[/latex] u relaciji [latex]\sim[/latex] akko [latex]a+d=b+c[/latex] (primjeti da vrijedi [latex]a-b=c-d[/latex], ali mi u tom trenu "ne znamo" oduzimati).
Probaj dokazati da je [latex]\sim[/latex] relacija ekvivalencije sam/sama. Javi ako negdje zapneš.
[quote="Black Mamba"]Konstruirajte bijekciju sa skupa N × N u skup N × Z. Konstruirajte bijekciju sa skupa N × Z u skup Z × Z.[/quote]
Ako si bio/bila na predavanju, znao/znala bi da postoji vrlo jednostavna bijekcija s [latex]\mathbb{N}[/latex] na [latex]\mathbb{Z}[/latex] (nazovimo ju [latex]f[/latex]). Koristeći tu bijekciju, možemo lako konstruirati bijekciju s [latex]\mathbb{N}\times\mathbb{N}[/latex] na [latex]\mathbb{N}\times\mathbb{Z}[/latex] ([latex](a,b)\mapsto(a,f(b))[/latex]).
Vjerojatno možeš onda sam/sama konstrurati bijekciju za drugi dio zadatka.
[quote="eve"]@Pmli
sve mi je jasno osim kaj ne kuzim kaj ce nam ovo:
[latex] 429108757\equiv4291087\cdot100+57\equiv57\equiv1(mod~4)[/latex][/quote]
Treba ti da zaključiš [latex]3^{429108757}\equiv3(mod~10)[/latex] (rečenica nakon).
| meda (napisa): | | imam pitanje za 7 zadatak iz prošlogodišnjeg kolokvija(1. grupa)...ugl meni ispada p(x)=x i p(x)=x^2, al mi je to nekak sumnjivo...jel neko možda rješavao taj zadatak? |
Pretpostavljam da misliš na zadatak s 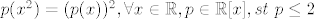 . Uzmeš da je . Uzmeš da je 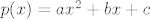 , uvrstiš u jednakost, dobiš pet jednadžbi: , uvrstiš u jednakost, dobiš pet jednadžbi: 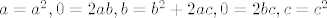 . Ideš po slučajevima: 1° . Ideš po slučajevima: 1° 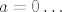 , 2° , 2° 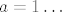
Dobiju se kao rješenja uz tvoje 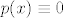 i i 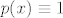 . .
| Black Mamba (napisa): | | Definirajte skup Z pomocu relacije ekvivalencije. Dokazite da je ta relacija doista relacija ekvivalencije. |
Ideja je da svaki cijeli broj možemo prikazati kao razliku dva prirodna. Nažalost, taj prikaz nije jedinstven. Stoga uvodimo relaciju kojom ćemo poistovijetiti neke razlike.
Promatramo skup 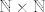 . Elementi tog skupa su parovi koje shvaćamo kao razlike: . Elementi tog skupa su parovi koje shvaćamo kao razlike: 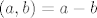 . Zato kažemo da su dva para . Zato kažemo da su dva para 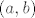 i i 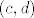 u relaciji u relaciji 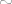 akko akko 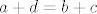 (primjeti da vrijedi (primjeti da vrijedi 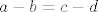 , ali mi u tom trenu "ne znamo" oduzimati). , ali mi u tom trenu "ne znamo" oduzimati).
Probaj dokazati da je 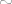 relacija ekvivalencije sam/sama. Javi ako negdje zapneš. relacija ekvivalencije sam/sama. Javi ako negdje zapneš.
| Black Mamba (napisa): | | Konstruirajte bijekciju sa skupa N × N u skup N × Z. Konstruirajte bijekciju sa skupa N × Z u skup Z × Z. |
Ako si bio/bila na predavanju, znao/znala bi da postoji vrlo jednostavna bijekcija s 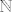 na na 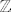 (nazovimo ju (nazovimo ju  ). Koristeći tu bijekciju, možemo lako konstruirati bijekciju s ). Koristeći tu bijekciju, možemo lako konstruirati bijekciju s 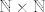 na na 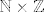 ( (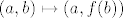 ). ).
Vjerojatno možeš onda sam/sama konstrurati bijekciju za drugi dio zadatka.
| eve (napisa): | @Pmli
sve mi je jasno osim kaj ne kuzim kaj ce nam ovo:
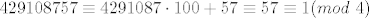 |
Treba ti da zaključiš  (rečenica nakon). (rečenica nakon).
|
|
| [Vrh] |
|
patlidzan
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (19:17:28)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
kikyca
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (18:45:07)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 0:17 čet, 14. 1. 2010 Naslov: Postano: 0:17 čet, 14. 1. 2010 Naslov: |
    |
|
|
ako je n paran, onda je n^2+2n-1 neparno => nije djeljivo s 4
ako je n neparan, onda se prikaze u obliku n^2+2n-1=(n+1)^2-2
sad, buduci je n neparan, imas da je n+1 paran (pa je kvadrat toga djeljiv s 4), a kad oduzmes 2 onda to ocito vise nije djeljivo s 4
ako je n paran, onda je n^2+2n-1 neparno => nije djeljivo s 4
ako je n neparan, onda se prikaze u obliku n^2+2n-1=(n+1)^2-2
sad, buduci je n neparan, imas da je n+1 paran (pa je kvadrat toga djeljiv s 4), a kad oduzmes 2 onda to ocito vise nije djeljivo s 4
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 0:24 čet, 14. 1. 2010 Naslov: Postano: 0:24 čet, 14. 1. 2010 Naslov: |
    |
|
|
[quote]4. Dokažite da je n-ti korijen iz 7 iracionalan broj [/quote]
Iz [latex]x=\sqrt[n]{7}\ \ /^{n}[/latex] slijedi [latex]x^{n}=7 \Rightarrow x^{n}-7=0[/latex]
[latex]\sqrt[n]{7}[/latex] je nultočka polinoma [latex]f(x)=x^{n}-7[/latex]
Kada bi taj polinom imao racionalnih nultočaka, one bi bile oblika [latex]\dipslaystyle\frac{p}{q}[/latex] za [latex]p \vert 7[/latex] i [latex]q \vert 1[/latex] (po teoremu o nultočkama polinoma s cjelobrojnim koeficijentima).
Slijedi da je [latex]p =\pm 1,\ \pm 7, q = \pm 1 [/latex].
Kandidati za cjelobrojne nultočke su onda [latex] 7,-7,1-1[/latex].
Uvrštavanjem vidimo da to nisu nultočke polinoma (naravno, za sve n > 1 gledamo, jer za n=1 imamo broj 7. koji naravno nije iracionalan).
Znači, za sve n > 1 f(x) nema racionalnih nultočaka pa [latex]\sqrt[n]{7}[/latex] nije racionalan broj.
[quote]Jel moze netko napisati rjesenje 6. zadatka 1. grupa... jer meni ispadne da je djeljivo s 4... [/quote]
Sličan zadatak je riješio pbakic na prošloj strani, ali pokušat ću i ja ovdje ako uspijem:
Pokažite da [latex]4 \nmid n^{2}+2n-1[/latex] za sve [latex]n \in \mathbb{N}[/latex].
Prvo provjeriš za parne brojeve, tj n=2k i dobiješ
[latex]4 \vert 4k^{2}+4k-1=2k(2k+2)-1[/latex], što je naravno nemoguće jer 4 ne dijeli neparne brojeve.
Sada i za neparne (n=2k-1):
[latex]4 \nmid 4k^{2}-4k+1+4k-2-1=4k^{2}-2[/latex], što opet ne vrijedi jer 4 dijeli [latex]4k^{2}[/latex], ali ne dijeli -2, pa ne dijeli niti [latex]4k^{2}-2[/latex].
Inače, zadatak se može riješiti pomoću kongruencija (dobije se isto rješenje naravno).
| Citat: | | 4. Dokažite da je n-ti korijen iz 7 iracionalan broj |
Iz 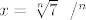 slijedi slijedi 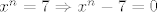
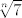 je nultočka polinoma je nultočka polinoma 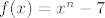
Kada bi taj polinom imao racionalnih nultočaka, one bi bile oblika 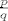 za za 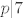 i i 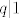 (po teoremu o nultočkama polinoma s cjelobrojnim koeficijentima). (po teoremu o nultočkama polinoma s cjelobrojnim koeficijentima).
Slijedi da je 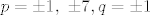 . .
Kandidati za cjelobrojne nultočke su onda 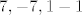 . .
Uvrštavanjem vidimo da to nisu nultočke polinoma (naravno, za sve n > 1 gledamo, jer za n=1 imamo broj 7. koji naravno nije iracionalan).
Znači, za sve n > 1 f(x) nema racionalnih nultočaka pa 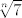 nije racionalan broj. nije racionalan broj.
| Citat: | | Jel moze netko napisati rjesenje 6. zadatka 1. grupa... jer meni ispadne da je djeljivo s 4... |
Sličan zadatak je riješio pbakic na prošloj strani, ali pokušat ću i ja ovdje ako uspijem:
Pokažite da 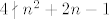 za sve za sve  . .
Prvo provjeriš za parne brojeve, tj n=2k i dobiješ
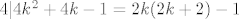 , što je naravno nemoguće jer 4 ne dijeli neparne brojeve. , što je naravno nemoguće jer 4 ne dijeli neparne brojeve.
Sada i za neparne (n=2k-1):
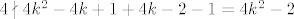 , što opet ne vrijedi jer 4 dijeli , što opet ne vrijedi jer 4 dijeli 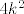 , ali ne dijeli -2, pa ne dijeli niti , ali ne dijeli -2, pa ne dijeli niti 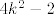 . .
Inače, zadatak se može riješiti pomoću kongruencija (dobije se isto rješenje naravno).
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
 Postano: 1:27 čet, 14. 1. 2010 Naslov: Postano: 1:27 čet, 14. 1. 2010 Naslov: |
    |
|
|
[quote="pmli"]
[quote="Black Mamba"]Definirajte skup Z pomocu relacije ekvivalencije. Dokazite da je ta relacija doista relacija ekvivalencije.[/quote]
Ideja je da svaki cijeli broj možemo prikazati kao razliku dva prirodna. Nažalost, taj prikaz nije jedinstven. Stoga uvodimo relaciju kojom ćemo poistovijetiti neke razlike.
Promatramo skup [latex]\mathbb{N}\times\mathbb{N}[/latex]. Elementi tog skupa su parovi koje shvaćamo kao razlike: [latex](a,b)=a-b[/latex]. Zato kažemo da su dva para [latex](a,b)[/latex] i [latex](c,d)[/latex] u relaciji [latex]\sim[/latex] akko [latex]a+d=b+c[/latex] (primjeti da vrijedi [latex]a-b=c-d[/latex], ali mi u tom trenu "ne znamo" oduzimati).
Probaj dokazati da je [latex]\sim[/latex] relacija ekvivalencije sam/sama. Javi ako negdje zapneš.
[/quote]
Znam dalje sama,hvala!!
Ovako sam ga i postavila,kao mogući način rješavanja,ali nisan bila sigurna jel to zapravo to šta se traži.
[quote="pmli"]
[quote="Black Mamba"]Konstruirajte bijekciju sa skupa N × N u skup N × Z. Konstruirajte bijekciju sa skupa N × Z u skup Z × Z.[/quote]
Ako si bio/bila na predavanju, znao/znala bi da postoji vrlo jednostavna bijekcija s [latex]\mathbb{N}[/latex] na [latex]\mathbb{Z}[/latex] (nazovimo ju [latex]f[/latex]). Koristeći tu bijekciju, možemo lako konstruirati bijekciju s [latex]\mathbb{N}\times\mathbb{N}[/latex] na [latex]\mathbb{N}\times\mathbb{Z}[/latex] ([latex](a,b)\mapsto(a,f(b))[/latex]).
Vjerojatno možeš onda sam/sama konstrurati bijekciju za drugi dio zadatka. [/quote]
Da,mogu! I da,sad se i sjećam ovog sa predavanja,al nisam bila zapisala,pa mi nije ni palo na pamet. :oops:
Inače...bila,znala ;)
Hvala puno,zbilja! :D
| pmli (napisa): |
| Black Mamba (napisa): | | Definirajte skup Z pomocu relacije ekvivalencije. Dokazite da je ta relacija doista relacija ekvivalencije. |
Ideja je da svaki cijeli broj možemo prikazati kao razliku dva prirodna. Nažalost, taj prikaz nije jedinstven. Stoga uvodimo relaciju kojom ćemo poistovijetiti neke razlike.
Promatramo skup 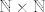 . Elementi tog skupa su parovi koje shvaćamo kao razlike: . Elementi tog skupa su parovi koje shvaćamo kao razlike: 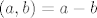 . Zato kažemo da su dva para . Zato kažemo da su dva para 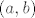 i i 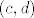 u relaciji u relaciji 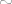 akko akko 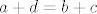 (primjeti da vrijedi (primjeti da vrijedi 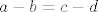 , ali mi u tom trenu "ne znamo" oduzimati). , ali mi u tom trenu "ne znamo" oduzimati).
Probaj dokazati da je 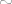 relacija ekvivalencije sam/sama. Javi ako negdje zapneš. relacija ekvivalencije sam/sama. Javi ako negdje zapneš.
|
Znam dalje sama,hvala!!
Ovako sam ga i postavila,kao mogući način rješavanja,ali nisan bila sigurna jel to zapravo to šta se traži.
| pmli (napisa): |
| Black Mamba (napisa): | | Konstruirajte bijekciju sa skupa N × N u skup N × Z. Konstruirajte bijekciju sa skupa N × Z u skup Z × Z. |
Ako si bio/bila na predavanju, znao/znala bi da postoji vrlo jednostavna bijekcija s 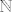 na na 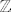 (nazovimo ju (nazovimo ju  ). Koristeći tu bijekciju, možemo lako konstruirati bijekciju s ). Koristeći tu bijekciju, možemo lako konstruirati bijekciju s 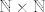 na na 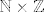 ( (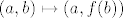 ). ).
Vjerojatno možeš onda sam/sama konstrurati bijekciju za drugi dio zadatka. |
Da,mogu! I da,sad se i sjećam ovog sa predavanja,al nisam bila zapisala,pa mi nije ni palo na pamet. 
Inače...bila,znala 
Hvala puno,zbilja! 
|
|
| [Vrh] |
|
andra
Forumaš(ica)

Pridružen/a: 02. 11. 2009. (19:23:23)
Postovi: (4F)16
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
 Postano: 13:15 čet, 14. 1. 2010 Naslov: Postano: 13:15 čet, 14. 1. 2010 Naslov: |
    |
|
|
ako je f(p/q)=0
f(x)=(x-p/q)(x^(n-1)a(n)+x^(n-2)a(n-1)+..........+a1)
f(x)=x^na(n)+x^(n-1)a(n-1)+..........+xa1-p/q(x^(n-1))a(n)-p/q(x^(n-2))a(n-1)+................+(p/q)a1
sada iz zadatka znamo da je an element Z n{1,2,3...........} i p,q element Z.....................
onda imamo pitanje zapravo da li p|(p*a1)/q...............što je onda očito valjda istina
Je. (p*a1)/q je cijeli broj, a kako su p i q rel. prosti, slijedi da q|a1. Sad je očito (p*a1)/q višekratnik od p, a time p|(p*a1)/q
ako je f(p/q)=0
f(x)=(x-p/q)(x^(n-1)a(n)+x^(n-2)a(n-1)+..........+a1)
f(x)=x^na(n)+x^(n-1)a(n-1)+..........+xa1-p/q(x^(n-1))a(n)-p/q(x^(n-2))a(n-1)+................+(p/q)a1
sada iz zadatka znamo da je an element Z n{1,2,3...........} i p,q element Z.....................
onda imamo pitanje zapravo da li p|(p*a1)/q...............što je onda očito valjda istina
Je. (p*a1)/q je cijeli broj, a kako su p i q rel. prosti, slijedi da q|a1. Sad je očito (p*a1)/q višekratnik od p, a time p|(p*a1)/q
|
|
| [Vrh] |
|
kikyca
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (18:45:07)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
|















