| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
mariola259
Forumaš(ica)

Pridružen/a: 31. 10. 2009. (12:58:48)
Postovi: (8)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 22:56 uto, 19. 1. 2010 Naslov: Postano: 22:56 uto, 19. 1. 2010 Naslov: |
    |
|
|
...nikad mi nije bilo jasno ZAŠTO svi čekate zadnju večer... :lol:
10. zadatak:
Tetiva parabole [latex]q...y^2=8x[/latex] je paralelna s pravcem [latex]p_1...2x -2y-3=0[/latex], a sadrži točku [latex]T(2, -4)[/latex]. Kako je tetiva paralelna s danim pravcem, onda je koeficijent smjera pravca na kojem leži tangenta jednak koeficijentu smjera danog pravca.
[latex]2x-2y=3 \\
-2y=-2x+3 \\
p_1...y = x - \frac{3}{2} \\
k = 1[/latex]
Dakle, tražimo pravac koji sadrži točku [latex]T(2, -4)[/latex], a ima koeficijent smjera [latex]k=1[/latex]. Nađimo jednadžbu pravca na kojem leži tetiva:
[latex]y-y_0 = k (x-x_0) \\
y+4=x-2 \\
p_2...y = x-6 [/latex]
Tražimo drugu točku kao sjecište pravca i parabole, odnosno [latex]p_2 \cap q[/latex]:
[latex](x-6)^2=8x \\
x^2 - 12x+36 = 8x \\
x^2 - 20x + 36 = 0 \\
x_1 = 18 \\
x_2 = 2 [/latex]
Ovu apscisu [latex]x_2 = 2[/latex] već imamo, pa nam ona nije interesantna (premda ona određuje dvije točke na paraboli...ali jedna od njih nije na pravcu na kojoj leži tetiva).
Točka koja nas zanima je [latex]P(18, 12)[/latex].
Sad iskoristimo formulu za udaljenost dviju točaka i dobijemo da je udaljenost [latex]d(T, P) = 16\sqrt{2}[/latex].
...nikad mi nije bilo jasno ZAŠTO svi čekate zadnju večer... 
10. zadatak:
Tetiva parabole 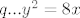 je paralelna s pravcem je paralelna s pravcem 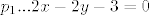 , a sadrži točku , a sadrži točku 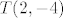 . Kako je tetiva paralelna s danim pravcem, onda je koeficijent smjera pravca na kojem leži tangenta jednak koeficijentu smjera danog pravca. . Kako je tetiva paralelna s danim pravcem, onda je koeficijent smjera pravca na kojem leži tangenta jednak koeficijentu smjera danog pravca.
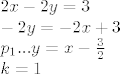
Dakle, tražimo pravac koji sadrži točku 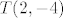 , a ima koeficijent smjera , a ima koeficijent smjera 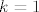 . Nađimo jednadžbu pravca na kojem leži tetiva: . Nađimo jednadžbu pravca na kojem leži tetiva:
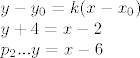
Tražimo drugu točku kao sjecište pravca i parabole, odnosno 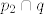 : :
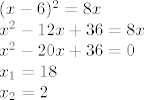
Ovu apscisu 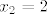 već imamo, pa nam ona nije interesantna (premda ona određuje dvije točke na paraboli...ali jedna od njih nije na pravcu na kojoj leži tetiva). već imamo, pa nam ona nije interesantna (premda ona određuje dvije točke na paraboli...ali jedna od njih nije na pravcu na kojoj leži tetiva).
Točka koja nas zanima je 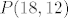 . .
Sad iskoristimo formulu za udaljenost dviju točaka i dobijemo da je udaljenost 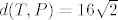 . .
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
Anna Lee
Forumaš(ica)


Pridružen/a: 11. 07. 2008. (00:49:44)
Postovi: (114)16
Spol: 
Lokacija: Zagreb
|
 Postano: 23:01 uto, 19. 1. 2010 Naslov: Postano: 23:01 uto, 19. 1. 2010 Naslov: |
    |
|
|
[quote]...nikad mi nije bilo jasno ZAŠTO svi čekate zadnju večer...[/quote]
pa iskreno, ni meni isto, al uvijek me nekak doceka to zavrsno ucenje do 3-4 :lol:
khm, imam problem sa 11.
jedna tangenta mi ispadne y=(1/3)x+3, a druga...nesto cudno :shock:
jel je opce ima? kak da to otkrijem? :oops:
edit: ha! jesu 4 tangente? y=(1/3)x+-3?
opet ne znam dalje :/
edit2: ne! ipak su dvije! jelda? :shock:
parabola ima tjeme u ishodistu, kruznica srediste...dakle 2 tangentice.
opet me muci kak da dodem do druge. :cry: heeeeeeeeeeeeeelp
| Citat: | | ...nikad mi nije bilo jasno ZAŠTO svi čekate zadnju večer... |
pa iskreno, ni meni isto, al uvijek me nekak doceka to zavrsno ucenje do 3-4 
khm, imam problem sa 11.
jedna tangenta mi ispadne y=(1/3)x+3, a druga...nesto cudno 
jel je opce ima? kak da to otkrijem? 
edit: ha! jesu 4 tangente? y=(1/3)x+-3?
opet ne znam dalje 
edit2: ne! ipak su dvije! jelda? 
parabola ima tjeme u ishodistu, kruznica srediste...dakle 2 tangentice.
opet me muci kak da dodem do druge.  heeeeeeeeeeeeeelp heeeeeeeeeeeeeelp
_________________
"The tooth fairy teaches children that they can sell body parts for money."
Zadnja promjena: Anna Lee; 23:33 uto, 19. 1. 2010; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
teapot
Forumaš(ica)
Pridružen/a: 12. 02. 2009. (22:01:19)
Postovi: (36)16
|
|
| [Vrh] |
|
prasac
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (23:13:17)
Postovi: (5)16
|
|
| [Vrh] |
|
z3h
Forumaš(ica)
Pridružen/a: 05. 10. 2004. (22:26:02)
Postovi: (46)16
|
|
| [Vrh] |
|
teapot
Forumaš(ica)
Pridružen/a: 12. 02. 2009. (22:01:19)
Postovi: (36)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
keko
Forumaš(ica)
Pridružen/a: 23. 11. 2009. (14:30:24)
Postovi: (16)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
mawa
Forumaš(ica)

Pridružen/a: 11. 10. 2009. (13:18:04)
Postovi: (13)16
Spol: 
|
|
| [Vrh] |
|
Anna Lee
Forumaš(ica)


Pridružen/a: 11. 07. 2008. (00:49:44)
Postovi: (114)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
teapot
Forumaš(ica)
Pridružen/a: 12. 02. 2009. (22:01:19)
Postovi: (36)16
|
|
| [Vrh] |
|
nitko_nezna
Forumaš(ica)

Pridružen/a: 10. 01. 2010. (15:53:34)
Postovi: (5)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 1:28 sri, 20. 1. 2010 Naslov: Postano: 1:28 sri, 20. 1. 2010 Naslov: |
    |
|
|
Imajte na umu da je Kenny ovo gradivo položio prije puuuno godina i da mu je rad u osnovnoj školi već počeo ubijati znanje iz ovog područja. Ovo mi dođe kao podsjetnik. :)
Anyway, ovaj [b]15. zadatak [/b]me zbunio... Krenuo sam na jedan način i onda skužio da sam krivo protumačio zadatak... :/ Odustajem od njega za večeras jerbo ujutro imam nastavu...
Zato evo [b]6. zadatak[/b] (btw, nek to netko još provjeri da ne bi bilo......):
Prvo ćemo jednadžbu hiperbole malo transformirati [latex]h...\frac{x^2}{20} - \frac{y^2}{5} = 1[/latex]. Iz toga iščitavamo da je [latex]a = \sqrt{20}, b=\sqrt{5}[/latex].
Znamo da su jednadžbe asimptota hiperbole [latex]a_{1, 2}...y = \pm \frac{b}{a}x[/latex], pa dobijemo da su asimptote [latex]a_{1, 2}...y = \pm \frac{1}{2}x[/latex].
Pravac koji je paralelan sa y-osi, a prolazi točkom (10, 3) je [latex]x = 10[/latex]. Taj pravac presječemo sa asimptotama i dobijemo točke [latex]T_1 = (10, 5), T_2 = (10, -5)[/latex].
Moramo odrediti tangentu na hiperbolu iz te dvije točke. Ovo je sada jedan malo gadniji dio. Za svaku ćemo točku dobiti po dvije tangente. U konačnici će to značiti da ćemo dobiti 4 sjecišta tangenata.
Pravac (tangenta) koja prolazi kroz točku T_1 ima jednadžbu [latex]5 = 10k +l[/latex]. Uvjet dodira pravca i hiperbole je [latex]a^2k^2+b^2=l^2[/latex], odnosno [latex]20k^2+5=l^2[/latex]. Imamo dakle dvije jednadžbe sa dvije nepoznanice.
Analogno odredimo i za drugu točku.
Dobijemo tangente, pa nađemo sjecišta tih tangenti.
p.s. Uvidio sam da negdje imam grešku. Ne znam gdje. Idem spavati jerbo ujutro radim. Nadam se da sam pomogao barem u ideji.
EDIT: ok, imao ja grešku u računu na papiru... dakle... Iz ove dvije jednadžbe gore dobijemo 2 tangente: [latex]t_1...y=\frac{3}{4}x - \frac{5}{2}, t_2...y=\frac{1}{2}x[/latex]. Neka vas ne buni ova druga tangenta, tj. to što smo dobili da je druga tangenta ustvari jedna od asimptota hiperbole. Naime, tu asimptotu možemo promatrati kao tangentu na hiperbolu, a tangira hiperbolu u nekoj beskonačno dalekoj točki.
[size=9][color=#999999]Added after 38 minutes:[/color][/size]
Evo još [b]1. zadatak[/b], a onda stvarno idem u krpe. :)
Dakle, veli da tražena kružnica prolazi točkama [latex]A(0,6), B(0, 0)[/latex], a tangenta je [latex]t...y=\frac{3}{4}x-\frac{25}{4}[/latex].
Uvjet dodira kružnice i tangente je [latex]r^2(1+k^2)=l^2[/latex]. Kad uvrstimo [latex]k=\frac{3}{4}, l=\frac{-25}{4}[/latex] dobijemo da je [latex]r=5[/latex].
E sad...kružnica je po definiciji skup točaka u ravnini jednako udaljenih od fiksne točke. Ako je [latex]A[/latex] udaljena od središta za [latex]r[/latex], onda je i središte udaljeno od točke [latex]A[/latex] za [latex]r[/latex]. Isto vrijedi i za točku [latex]B[/latex]. Ono što hoću reći jest: moramo odrediti središte tražene kružnice, a to ćemo napraviti tako da odredimo sjecište dviju kružnica (kojima su središta [latex]A[/latex], odnosno [latex]B[/latex], a imaju radijus [latex]r[/latex]).
U konačnici dobijemo dva moguća središta: [latex]S_1(-4, 3)[/latex] i [latex]S_2(4, 3)[/latex]. Nama odgovara samo ova druga kružnica, odnosno ona kojoj je jednadžba [latex]k...(x-4)^2+(y-3)^2 = 25[/latex].
Laku noć ;)
Imajte na umu da je Kenny ovo gradivo položio prije puuuno godina i da mu je rad u osnovnoj školi već počeo ubijati znanje iz ovog područja. Ovo mi dođe kao podsjetnik. 
Anyway, ovaj 15. zadatak me zbunio... Krenuo sam na jedan način i onda skužio da sam krivo protumačio zadatak...  Odustajem od njega za večeras jerbo ujutro imam nastavu... Odustajem od njega za večeras jerbo ujutro imam nastavu...
Zato evo 6. zadatak (btw, nek to netko još provjeri da ne bi bilo......):
Prvo ćemo jednadžbu hiperbole malo transformirati 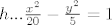 . Iz toga iščitavamo da je . Iz toga iščitavamo da je 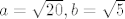 . .
Znamo da su jednadžbe asimptota hiperbole 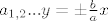 , pa dobijemo da su asimptote , pa dobijemo da su asimptote 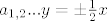 . .
Pravac koji je paralelan sa y-osi, a prolazi točkom (10, 3) je  . Taj pravac presječemo sa asimptotama i dobijemo točke . Taj pravac presječemo sa asimptotama i dobijemo točke 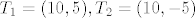 . .
Moramo odrediti tangentu na hiperbolu iz te dvije točke. Ovo je sada jedan malo gadniji dio. Za svaku ćemo točku dobiti po dvije tangente. U konačnici će to značiti da ćemo dobiti 4 sjecišta tangenata.
Pravac (tangenta) koja prolazi kroz točku T_1 ima jednadžbu 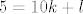 . Uvjet dodira pravca i hiperbole je . Uvjet dodira pravca i hiperbole je 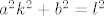 , odnosno , odnosno 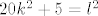 . Imamo dakle dvije jednadžbe sa dvije nepoznanice. . Imamo dakle dvije jednadžbe sa dvije nepoznanice.
Analogno odredimo i za drugu točku.
Dobijemo tangente, pa nađemo sjecišta tih tangenti.
p.s. Uvidio sam da negdje imam grešku. Ne znam gdje. Idem spavati jerbo ujutro radim. Nadam se da sam pomogao barem u ideji.
EDIT: ok, imao ja grešku u računu na papiru... dakle... Iz ove dvije jednadžbe gore dobijemo 2 tangente: 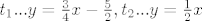 . Neka vas ne buni ova druga tangenta, tj. to što smo dobili da je druga tangenta ustvari jedna od asimptota hiperbole. Naime, tu asimptotu možemo promatrati kao tangentu na hiperbolu, a tangira hiperbolu u nekoj beskonačno dalekoj točki. . Neka vas ne buni ova druga tangenta, tj. to što smo dobili da je druga tangenta ustvari jedna od asimptota hiperbole. Naime, tu asimptotu možemo promatrati kao tangentu na hiperbolu, a tangira hiperbolu u nekoj beskonačno dalekoj točki.
Added after 38 minutes:
Evo još 1. zadatak, a onda stvarno idem u krpe. 
Dakle, veli da tražena kružnica prolazi točkama 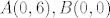 , a tangenta je , a tangenta je 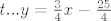 . .
Uvjet dodira kružnice i tangente je 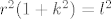 . Kad uvrstimo . Kad uvrstimo 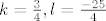 dobijemo da je dobijemo da je 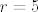 . .
E sad...kružnica je po definiciji skup točaka u ravnini jednako udaljenih od fiksne točke. Ako je  udaljena od središta za udaljena od središta za  , onda je i središte udaljeno od točke , onda je i središte udaljeno od točke  za za  . Isto vrijedi i za točku . Isto vrijedi i za točku  . Ono što hoću reći jest: moramo odrediti središte tražene kružnice, a to ćemo napraviti tako da odredimo sjecište dviju kružnica (kojima su središta . Ono što hoću reći jest: moramo odrediti središte tražene kružnice, a to ćemo napraviti tako da odredimo sjecište dviju kružnica (kojima su središta  , odnosno , odnosno  , a imaju radijus , a imaju radijus  ). ).
U konačnici dobijemo dva moguća središta: 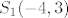 i i 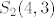 . Nama odgovara samo ova druga kružnica, odnosno ona kojoj je jednadžba . Nama odgovara samo ova druga kružnica, odnosno ona kojoj je jednadžba 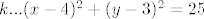 . .
Laku noć 
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
sanja25
Forumaš(ica)

Pridružen/a: 15. 12. 2009. (15:02:00)
Postovi: (1A)16
|
|
| [Vrh] |
|
munjotres
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (14:10:17)
Postovi: (2D)16
|
|
| [Vrh] |
|
|











