| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 21:42 čet, 21. 2. 2008 Naslov: |
    |
|
|
[quote]
x^2 - 4y^2 + 36 = 0
x^2 = 4y^2 - 36
djelovanje korijenom na jednadžbu uz uvjet:
4y^2 - 36 >= 0
za y@<-oo, -3]U[3,+oo>
zbog uvjeta iz zadatka y@[-4,4] vrijedi(presjek):
y@[-4,-3]U[3,4]
[/quote]
Sad sam tek skužila da je zadatak bio x^2-4y^2-36=0
pa je y iz [-4,4], a x iz [-10,-6]U[6,10].
| Citat: |
x^2 - 4y^2 + 36 = 0
x^2 = 4y^2 - 36
djelovanje korijenom na jednadžbu uz uvjet:
4y^2 - 36 >= 0
za y@←oo, -3]U[3,+oo>
zbog uvjeta iz zadatka y@[-4,4] vrijedi(presjek):
y@[-4,-3]U[3,4]
|
Sad sam tek skužila da je zadatak bio x^2-4y^2-36=0
pa je y iz [-4,4], a x iz [-10,-6]U[6,10].
|
|
| [Vrh] |
|
stuey
Forumaš(ica)
Pridružen/a: 03. 11. 2006. (15:52:11)
Postovi: (A2)16
Spol: 
Lokacija: Rijeka, Zg
|
| Postano: 22:05 čet, 21. 2. 2008 Naslov: |
|
|
|
[quote="Anonymous"]Moze li netko,molim vas,napisati kako je rjesio 2. zadatak iz zavrsnog?
hvala![/quote]
ja sam napisao x=(x_1, x_2, ..., x_n), y=(y_1, y_2, ..., y_n), zatim sam raspisao što znači onaj izraz u zagradi , a to je, kad se srede obje norme i sve, suma po i od (4*x_i^2 + 4*x_i*y_i + 2*y_i^2). označit ću tu sumu s (++) jer ću je još koristit ispod.
i onda sam izračunao parcijalne derivacije po x_i i y_i.
kad računam parc.derivaciju po x_i dobijem (8*x_i + 4*y_i) * cos(++), a kad računam parc.derivaciju po y_i dobijem (4*x_i + 4*y_i) * cos(++).
dakle dobio sam sve parcijalne derivacije, one postoje i neprekidne su, dakle funkcija f je u svim točkama domene diferencijabilna, a diferencijal je matrica gdje je parc.derivacija po x_i i y_i i-ti redak te matrice.
| Anonymous (napisa): | Moze li netko,molim vas,napisati kako je rjesio 2. zadatak iz zavrsnog?
hvala! |
ja sam napisao x=(x_1, x_2, ..., x_n), y=(y_1, y_2, ..., y_n), zatim sam raspisao što znači onaj izraz u zagradi , a to je, kad se srede obje norme i sve, suma po i od (4*x_i^2 + 4*x_i*y_i + 2*y_i^2). označit ću tu sumu s (++) jer ću je još koristit ispod.
i onda sam izračunao parcijalne derivacije po x_i i y_i.
kad računam parc.derivaciju po x_i dobijem (8*x_i + 4*y_i) * cos(++), a kad računam parc.derivaciju po y_i dobijem (4*x_i + 4*y_i) * cos(++).
dakle dobio sam sve parcijalne derivacije, one postoje i neprekidne su, dakle funkcija f je u svim točkama domene diferencijabilna, a diferencijal je matrica gdje je parc.derivacija po x_i i y_i i-ti redak te matrice.
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)
Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol:
Lokacija: |R^3
|
| Postano: 22:42 čet, 21. 2. 2008 Naslov: |
|
|
|
[quote="Anonymous"][quote]
x^2 - 4y^2 + 36 = 0
x^2 = 4y^2 - 36
djelovanje korijenom na jednadžbu uz uvjet:
4y^2 - 36 >= 0
za y@<-oo, -3]U[3,+oo>
zbog uvjeta iz zadatka y@[-4,4] vrijedi(presjek):
y@[-4,-3]U[3,4]
[/quote]
Sad sam tek skužila da je zadatak bio x^2-4y^2-36=0
pa je y iz [-4,4], a x iz [-10,-6]U[6,10].[/quote]
Ako je tako zadan zadatak onda ti je rješenje dobro. Bodove si dakle izgubila na nedostatku komentara. :(
| Anonymous (napisa): | | Citat: |
x^2 - 4y^2 + 36 = 0
x^2 = 4y^2 - 36
djelovanje korijenom na jednadžbu uz uvjet:
4y^2 - 36 >= 0
za y@←oo, -3]U[3,+oo>
zbog uvjeta iz zadatka y@[-4,4] vrijedi(presjek):
y@[-4,-3]U[3,4]
|
Sad sam tek skužila da je zadatak bio x^2-4y^2-36=0
pa je y iz [-4,4], a x iz [-10,-6]U[6,10]. |
Ako je tako zadan zadatak onda ti je rješenje dobro. Bodove si dakle izgubila na nedostatku komentara. 
_________________
...He never had looked less like captain of any-thing, even his own soul.
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)
Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)
Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
kika
Forumaš(ica)
Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
|
| [Vrh] |
|
Raz
Forumaš(ica)
Pridružen/a: 07. 02. 2005. (22:40:23)
Postovi: (6F)16
Lokacija: Tamo gdje ribe jedu avanturiste...
|
| Postano: 20:58 pon, 25. 2. 2008 Naslov: |
|
|
|
evo ja bio danas kod prof. tambace...prosao :D
pitanja su bila u globalu,ne samo meni,vec kako su ljudi pricali dok bi izlazili...
primjer neprekidne fje, diferencijabline,neprekidne koja nije
difernencijabilna...dokaz da ja odredjena fja neprekidna,al iz definicije(ne
iz limesa,vec preko delta,epsilon)
B-W.....A otvoren,f neprekidna dal je f(A) otvoren? isto to za
kompaktan,zatvoren
kompaktnost,karakterizacije
povezanost,povezanost putevima...neprekidna fja a povezan f(A)povezan
teorem koji govori fja dfb->f neprekidna(dokaz)
def diferencijabilnosti, jedinstvenost lin operatota(dokaz)
niz konvergira<=> kordinatni nizovi konvergiraju
fja neprekidna<=> kordinatne fje neprekidne
heineova krakt.neprekidnosti
iskaz teorema o inverznoj fji...za manju ocjenu treba znati objasnit, al ne dokazati...
teorem za srednje vrijednosti za realne i vektorske fje...
i tako... :)
uglavnom nije toliko ni vazno sve striktno znati od a do ž, vec je bitno razumjeti i povezivati gradivo...prof. je odlican ...danas su ga cak neki i uspjeli nasmijati svojim odgovorima...
evo ja bio danas kod prof. tambace...prosao 
pitanja su bila u globalu,ne samo meni,vec kako su ljudi pricali dok bi izlazili...
primjer neprekidne fje, diferencijabline,neprekidne koja nije
difernencijabilna...dokaz da ja odredjena fja neprekidna,al iz definicije(ne
iz limesa,vec preko delta,epsilon)
B-W.....A otvoren,f neprekidna dal je f(A) otvoren? isto to za
kompaktan,zatvoren
kompaktnost,karakterizacije
povezanost,povezanost putevima...neprekidna fja a povezan f(A)povezan
teorem koji govori fja dfb->f neprekidna(dokaz)
def diferencijabilnosti, jedinstvenost lin operatota(dokaz)
niz konvergira<=> kordinatni nizovi konvergiraju
fja neprekidna<=> kordinatne fje neprekidne
heineova krakt.neprekidnosti
iskaz teorema o inverznoj fji...za manju ocjenu treba znati objasnit, al ne dokazati...
teorem za srednje vrijednosti za realne i vektorske fje...
i tako... 
uglavnom nije toliko ni vazno sve striktno znati od a do ž, vec je bitno razumjeti i povezivati gradivo...prof. je odlican ...danas su ga cak neki i uspjeli nasmijati svojim odgovorima...
_________________
One good thing about music,when it hits: you feel no pain
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)
Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)
Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)
Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)
Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
| Postano: 10:35 uto, 26. 2. 2008 Naslov: |
|
|
|
[quote="Anonymous"]jel moze netko dati primjer za fju koja je,i neku koja nije neprekidna,te kako bi to dokazali preko delta,epsilon? (ovaj drugi dioodg mi jue bitniji)[/quote]
Ma definiraš fju nekak bezveze recimo:
f(x)=1 , x!=2
f(x)=6 , x=2.
I sad se pitaš dal je limes (x teži 2) f(x) = f(2) i dobiješ da je 1=6 što nije.
Neprekidna, nije difb je aps vrijednost tipičan primjer, ali i bilo koja druga koja ima 'špicu'.
| Anonymous (napisa): | | jel moze netko dati primjer za fju koja je,i neku koja nije neprekidna,te kako bi to dokazali preko delta,epsilon? (ovaj drugi dioodg mi jue bitniji) |
Ma definiraš fju nekak bezveze recimo:
f(x)=1 , x!=2
f(x)=6 , x=2.
I sad se pitaš dal je limes (x teži 2) f(x) = f(2) i dobiješ da je 1=6 što nije.
Neprekidna, nije difb je aps vrijednost tipičan primjer, ali i bilo koja druga koja ima 'špicu'.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy |
|
| [Vrh] |
|
desire
Forumaš(ica)
Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
| Postano: 16:45 uto, 26. 2. 2008 Naslov: |
|
|
|
[quote="desire"]Ima neka dobra dusa da mi malo pojasni dokaze korolara 8.8 i teorema 8.10?
[/quote]
Naravno da ima ;)
Tm 8.8 a pov putevima -> A povezan.
P.s. A pov putevima & nije pov
Pošto nije povezan onda postoje neprazni U i V otv, UuV=A, UpresjekV=0.
Uzmemo u iz U & v iz V. (te točke postoje jer su U,V neprazni). A je pov putevima pa postoji put između u & v : [latex]\alpha:[a,b]->A [/latex]
[latex]\alpha (a) = u , \alpha (b) = v[/latex]
Sada su [latex]\alpha^{-1} (U) , \alpha^{-1} (V)[/latex] (praslike po alfa) neprazni, disj i njihova unija je [a,b] ([latex] \alpha^{-1}(U) u \alpha^{-1}(V) = \alpha^{-1}( UuV) = \alpha^{-1}(A)=[a,b][/latex] ).
Tu dolazimo do kontradikcije jer je segment povezan.
8.10. Tu opet slično. Pretp suprotno i nađeš skupove u kodomeni koja nije povezana i onda opet preko praslika dobiješ kontadikciju sa povezanosti od A.
| desire (napisa): | Ima neka dobra dusa da mi malo pojasni dokaze korolara 8.8 i teorema 8.10?
|
Naravno da ima 
Tm 8.8 a pov putevima → A povezan.
P.s. A pov putevima & nije pov
Pošto nije povezan onda postoje neprazni U i V otv, UuV=A, UpresjekV=0.
Uzmemo u iz U & v iz V. (te točke postoje jer su U,V neprazni). A je pov putevima pa postoji put između u & v :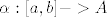 
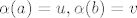
Sada su 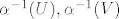 (praslike po alfa) neprazni, disj i njihova unija je [a,b] ( ).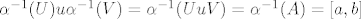
Tu dolazimo do kontradikcije jer je segment povezan.
8.10. Tu opet slično. Pretp suprotno i nađeš skupove u kodomeni koja nije povezana i onda opet preko praslika dobiješ kontadikciju sa povezanosti od A.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy |
|
| [Vrh] |
|
desire
Forumaš(ica)
Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol:
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)
Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol:
Lokacija: |R^3
|
| Postano: 9:13 sri, 27. 2. 2008 Naslov: |
|
|
|
[quote="Anonymous"]imam pitanje i molio bih što priji odgovor ako je moguće jer imam usmeni za 2 sata... :(
bilo je pitanje ako je A otvoren, f neprekidna, da li je f8A) otv?šta tu reći, na što se pozvati?
hvala[/quote]
Pozovi se na, [i]good old[/i], realnu konstantu na IR.
(A=IR otvoren, slika jednočlan skup dakle zatvoren)
| Anonymous (napisa): | imam pitanje i molio bih što priji odgovor ako je moguće jer imam usmeni za 2 sata...
bilo je pitanje ako je A otvoren, f neprekidna, da li je f8A) otv?šta tu reći, na što se pozvati?
hvala |
Pozovi se na, good old, realnu konstantu na IR.
(A=IR otvoren, slika jednočlan skup dakle zatvoren)
_________________
...He never had looked less like captain of any-thing, even his own soul.
|
|
| [Vrh] |
|
|
