|
[quote="eve"]@Grga. Tnx na odgovoru. Zanima me jos kako ja to mogu precizno ("matematicki") napisat, i zanima me zasto isto nisi zakljucio i za r(A),jer retci od AB su ln kombinacija redaka od A?[/quote]
Ako je AB = C, tada vrijedi
[latex]\displaystyle c_{i,k} = \sum_{j = 1}^n a_{i, j}b_{j, k}[/latex]
Sad vidis da koeficijenti elemenata iz matrice A ne ovise o k, a svi koeficijenti elemenata iz matrice b imaju k (dakle raj je element od c linearna kombinacija elemenata od b koji se nalaze u k-tom stupcu). Ako uzmes k =1, ..., r . Onda je i-ti redak od c jednak:
[latex]\displaystyle c_i = \sum_{j = 1}^n a_{i, j}b_j[/latex]
odnosno to sto smo rekli. Stvar je zapravo po definiciji samo si moras malo drukcije posloziti.. A za A vrijedi analogno, ali su ovaj put [b]stupci[/b] od AB linearna kombinacija stupaca od A
| eve (napisa): | | @Grga. Tnx na odgovoru. Zanima me jos kako ja to mogu precizno ("matematicki") napisat, i zanima me zasto isto nisi zakljucio i za r(A),jer retci od AB su ln kombinacija redaka od A? |
Ako je AB = C, tada vrijedi
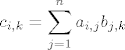
Sad vidis da koeficijenti elemenata iz matrice A ne ovise o k, a svi koeficijenti elemenata iz matrice b imaju k (dakle raj je element od c linearna kombinacija elemenata od b koji se nalaze u k-tom stupcu). Ako uzmes k =1, ..., r . Onda je i-ti redak od c jednak:
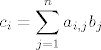
odnosno to sto smo rekli. Stvar je zapravo po definiciji samo si moras malo drukcije posloziti.. A za A vrijedi analogno, ali su ovaj put stupci od AB linearna kombinacija stupaca od A
_________________
Bri
|






