| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
andra
Forumaš(ica)

Pridružen/a: 02. 11. 2009. (19:23:23)
Postovi: (4F)16
|
 Postano: 13:50 čet, 14. 1. 2010 Naslov: Postano: 13:50 čet, 14. 1. 2010 Naslov: |
    |
|
|
[quote="ante c"]ako je f(p/q)=0
f(x)=(x-p/q)(x^(n-1)a(n)+x^(n-2)a(n-1)+..........+a1)
f(x)=x^na(n)+x^(n-1)a(n-1)+..........+xa1-p/q(x^(n-1))a(n)-p/q(x^(n-2))a(n-1)+................+(p/q)a1
sada iz zadatka znamo da je an element Z n{1,2,3...........} i p,q element Z.....................
onda imamo pitanje zapravo da li p|(p*a1)/q...............što je onda očito valjda istina
Je. (p*a1)/q je cijeli broj, a kako su p i q rel. prosti, slijedi da q|a1. Sad je očito (p*a1)/q višekratnik od p, a time p|(p*a1)/q[/quote]
ok vidla sam to rijesenje, ali mene i dalje zanima dali se moze i na onaj nacin ili ne??
| ante c (napisa): | ako je f(p/q)=0
f(x)=(x-p/q)(x^(n-1)a(n)+x^(n-2)a(n-1)+..........+a1)
f(x)=x^na(n)+x^(n-1)a(n-1)+..........+xa1-p/q(x^(n-1))a(n)-p/q(x^(n-2))a(n-1)+................+(p/q)a1
sada iz zadatka znamo da je an element Z n{1,2,3...........} i p,q element Z.....................
onda imamo pitanje zapravo da li p|(p*a1)/q...............što je onda očito valjda istina
Je. (p*a1)/q je cijeli broj, a kako su p i q rel. prosti, slijedi da q|a1. Sad je očito (p*a1)/q višekratnik od p, a time p|(p*a1)/q |
ok vidla sam to rijesenje, ali mene i dalje zanima dali se moze i na onaj nacin ili ne??
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 15:01 čet, 14. 1. 2010 Naslov: Postano: 15:01 čet, 14. 1. 2010 Naslov: |
    |
|
|
[quote]Kako se rjesava 3. i 4. zadatak 1. grupa[/quote]
Evo, za 4. zadatak, je zapravo vrlo jednostavan dokaz, radili smo ga na predavanjima, a i ima u knjizi, ali tko nema ni knjige ni bilježnice:
Znamo kako se definiraju elementarni i Newtonovi polinomi u dvije varijable:
[latex]\sigma_{1}=x+y,\ \sigma_{2}=x\cdot y[/latex]
[latex]S_{k-1}=x^{k-1}+y^{k-1},\ S_{k-2}=x^{k-2}+y^{k-2}[/latex]
Sada uvrstimo u početnu jednandžbu:
[latex]S_{k}=\sigma_{1}S_{k-1}-\sigma_{2}S_{k-2}=(x+y)(x^{k-1}+y^{k-1})-xy(x^{k-2}+y^{k-2})=[/latex]
[latex]=x^{k}+xy^{k-1}+yx^{k-1}+y^{k}-yx^{k-1}-xy^{k-1}=x^{k}+y^{k}[/latex]
To bi bilo to.
| Citat: | | Kako se rjesava 3. i 4. zadatak 1. grupa |
Evo, za 4. zadatak, je zapravo vrlo jednostavan dokaz, radili smo ga na predavanjima, a i ima u knjizi, ali tko nema ni knjige ni bilježnice:
Znamo kako se definiraju elementarni i Newtonovi polinomi u dvije varijable:
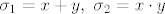
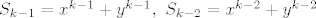
Sada uvrstimo u početnu jednandžbu:
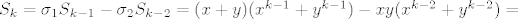
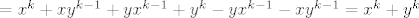
To bi bilo to.
Zadnja promjena: Genaro; 18:47 čet, 14. 1. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
andra
Forumaš(ica)

Pridružen/a: 02. 11. 2009. (19:23:23)
Postovi: (4F)16
|
|
| [Vrh] |
|
mare
Forumaš(ica)

Pridružen/a: 01. 11. 2009. (20:20:21)
Postovi: (11)16
Spol: 
|
|
| [Vrh] |
|
andra
Forumaš(ica)

Pridružen/a: 02. 11. 2009. (19:23:23)
Postovi: (4F)16
|
|
| [Vrh] |
|
gramzon
Forumaš(ica)

Pridružen/a: 09. 07. 2009. (20:11:44)
Postovi: (3B)16
Spol: 
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
ananas
Forumaš(ica)

Pridružen/a: 28. 10. 2009. (17:56:24)
Postovi: (34)16
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 20:57 čet, 14. 1. 2010 Naslov: Postano: 20:57 čet, 14. 1. 2010 Naslov: |
    |
|
|
[quote="patlidzan"]1. Odredite umnožak n-tih korijena broja -3 ( pomoću Vietovih formula)[/quote]
Ti korijeni su nultočke polinoma [latex]x^n+3[/latex]. Po Vieteovim formulama slijedi [latex]x_1\cdot\ldots\cdot x_n=(-1)^{n}3[/latex].
[quote="patlidzan"]2.Neka su m i n neparni prirodni brojevi takvi da je m>n+2. Dokažite a ne postoji polinom p element Z[x] takav da je p(m)-p(n) prost broj[/quote]
Tvrdnja koja puno pomaže kod ovakvih zadataka: [latex](\forall p \in \mathbb{Z}[x])(\forall k, l \in \mathbb{Z})~k-l|p(k)-p(l)[/latex]. Probaj to sam/a dokazat (samo raspišeš sa [latex]p(x)=a_n x^n + \ldots + a_0[/latex], malo grupiraš...). Kad to primjeniš na ovaj zadatak, slijedilo bi da prost broj mora biti dijeljiv s parnim brojem strogo većim od 2.
[quote="patlidzan"]3. Kako bi izračunali mjeru: M(3^4102-3^2113,3^4105-3^2113)[/quote]
Prvo primjenimo jednakost [latex]M(a,b)=M(a,b-a)[/latex]. Dobimo [latex]M(3^{4102}-3^{2113},3^{4105}-3^{4102})=M(3^{4102}-3^{2113},26 \cdot 3^{4102})[/latex]. Zatim se sjetimo da je [latex]M(na,nb)=nM(a,b)[/latex]. Slijedi [latex]M(3^{4102}-3^{2113},26 \cdot 3^{4102})=3^{2113} M(3^{1989}-1,26 \cdot 3^{1989})[/latex]. [latex]3^{1989}-1[/latex] nije djeljivo s [latex]3[/latex], pa se to svodi na [latex]3^{2113} M(3^{1989}-1,26)=3^{2113} M(27^{663}-1,26)=26 \cdot 3^{2113}[/latex].
[quote="andra"]dali se zadatak u kojem je zadano da su p i q relativno prosti cijeli brojevi i treba dokazat da p dijeli a0 dali se to moze ovako pokazati:
f(x)=an x^n+...+a1x+a0, ai e Z
f(p/q)=0 --> an(p/q)^n+...+a1(p/q)+a0=0
a0=-an(p/q)^n-...-a1(p/q)=(-p/q)(an(p/q)^n-1+...+a1) i sad znamo da je an(p/q)^n-1+...+a1 element Z...[/quote]
Možeš li malo argumentirati tu tvrdnju? Moj spori mozak to ne može prihvatiti.
[quote="andra"]...ali znamo i iz ovoga da p/q|a0...[/quote]
Od kad se relacija djeljivosti definira i za racionalne brojeve?
[quote="andra"]...a posto je M(p,q)=1 onda p/a0???
dali se to moze tako??[/quote]
:? :? :? Probaj se malo bolje izjasniti. Na predavanjima smo dokazivali tako da smo pomnožili u drugom retku s q^n.
| patlidzan (napisa): | | 1. Odredite umnožak n-tih korijena broja -3 ( pomoću Vietovih formula) |
Ti korijeni su nultočke polinoma 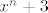 . Po Vieteovim formulama slijedi . Po Vieteovim formulama slijedi 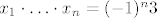 . .
| patlidzan (napisa): | | 2.Neka su m i n neparni prirodni brojevi takvi da je m>n+2. Dokažite a ne postoji polinom p element Z[x] takav da je p(m)-p(n) prost broj |
Tvrdnja koja puno pomaže kod ovakvih zadataka: 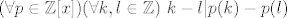 . Probaj to sam/a dokazat (samo raspišeš sa . Probaj to sam/a dokazat (samo raspišeš sa 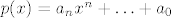 , malo grupiraš...). Kad to primjeniš na ovaj zadatak, slijedilo bi da prost broj mora biti dijeljiv s parnim brojem strogo većim od 2. , malo grupiraš...). Kad to primjeniš na ovaj zadatak, slijedilo bi da prost broj mora biti dijeljiv s parnim brojem strogo većim od 2.
| patlidzan (napisa): | | 3. Kako bi izračunali mjeru: M(3^4102-3^2113,3^4105-3^2113) |
Prvo primjenimo jednakost 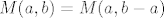 . Dobimo . Dobimo 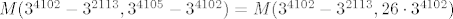 . Zatim se sjetimo da je . Zatim se sjetimo da je 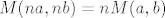 . Slijedi . Slijedi 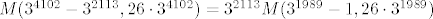 . . 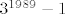 nije djeljivo s nije djeljivo s 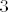 , pa se to svodi na , pa se to svodi na 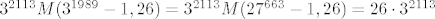 . .
| andra (napisa): | dali se zadatak u kojem je zadano da su p i q relativno prosti cijeli brojevi i treba dokazat da p dijeli a0 dali se to moze ovako pokazati:
f(x)=an x^n+...+a1x+a0, ai e Z
f(p/q)=0 → an(p/q)^n+...+a1(p/q)+a0=0
a0=-an(p/q)^n-...-a1(p/q)=(-p/q)(an(p/q)^n-1+...+a1) i sad znamo da je an(p/q)^n-1+...+a1 element Z... |
Možeš li malo argumentirati tu tvrdnju? Moj spori mozak to ne može prihvatiti.
| andra (napisa): | | ...ali znamo i iz ovoga da p/q|a0... |
Od kad se relacija djeljivosti definira i za racionalne brojeve?
| andra (napisa): | ...a posto je M(p,q)=1 onda p/a0???
dali se to moze tako?? |
   Probaj se malo bolje izjasniti. Na predavanjima smo dokazivali tako da smo pomnožili u drugom retku s q^n. Probaj se malo bolje izjasniti. Na predavanjima smo dokazivali tako da smo pomnožili u drugom retku s q^n.
Zadnja promjena: pmli; 21:34 čet, 14. 1. 2010; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
ananas
Forumaš(ica)

Pridružen/a: 28. 10. 2009. (17:56:24)
Postovi: (34)16
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
ananas
Forumaš(ica)

Pridružen/a: 28. 10. 2009. (17:56:24)
Postovi: (34)16
|
|
| [Vrh] |
|
Bole13
Forumaš(ica)
Pridružen/a: 01. 11. 2008. (00:33:50)
Postovi: (5A)16
Spol: 
|
|
| [Vrh] |
|
patlidzan
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (19:17:28)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
|















