| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ivancica
Forumaš(ica)
Pridružen/a: 10. 09. 2007. (10:18:25)
Postovi: (41)16
|
|
| [Vrh] |
|
ivancica
Forumaš(ica)
Pridružen/a: 10. 09. 2007. (10:18:25)
Postovi: (41)16
|
|
| [Vrh] |
|
teja
Forumaš(ica)
Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
teja
Forumaš(ica)
Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol:
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
kika
Forumaš(ica)
Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
|
| [Vrh] |
|
kika
Forumaš(ica)
Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
 Postano: 22:27 ned, 30. 3. 2008 Naslov: |
    |
|
|
[quote="kika"]1.radis parcijalnu integraciju,stavis da je u=(lnx)^2,a dv=1*dx --->dobijes da je du=2*lnx*x^-1 ,a v=x ....
sad imas I= x*(lnx)^2 - integral(x^-1 *x*2*lnx*dx)
pa opet napravis parcijalnu derivaciju[u=lnx,dv=1*dx --->du=x^-1*dx, v=x ]
i dobiva se I=x*(lnx)^2 -2x*lnx+2*integral(du*v),tj.
I=x*(lnx)^2 -2x*lnx+ 2*integral(1*dx),tj.
I=x*(lnx)^2 -2x*lnx+ 2*x
ps.rezultat je takav i u brojnstajnu :)
nadam se da sam pomogla:)[/quote]
| kika (napisa): | 1.radis parcijalnu integraciju,stavis da je u=(lnx)^2,a dv=1*dx →dobijes da je du=2*lnx*x^-1 ,a v=x ....
sad imas I= x*(lnx)^2 - integral(x^-1 *x*2*lnx*dx)
pa opet napravis parcijalnu derivaciju[u=lnx,dv=1*dx →du=x^-1*dx, v=x ]
i dobiva se I=x*(lnx)^2 -2x*lnx+2*integral(du*v),tj.
I=x*(lnx)^2 -2x*lnx+ 2*integral(1*dx),tj.
I=x*(lnx)^2 -2x*lnx+ 2*x
ps.rezultat je takav i u brojnstajnu 
nadam se da sam pomogla:) |
|
|
| [Vrh] |
|
teja
Forumaš(ica)
Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol:
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
kika
Forumaš(ica)
Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)
Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
| Postano: 20:22 sub, 5. 4. 2008 Naslov: |
|
|
|
U svim točkama osim nule funkcija signum (ta je bila zadana) je neprekidna pa je oscilacija nula. Sad promatramo okoline od nule. Svaka takva okolina sadrži barem jedan negativan i jedan pozitivan broj, tj. funkcija signum postiže vrijednosti -1,0,1 na takvoj okolini, pa je [latex]sup_{x_{1},x_{2} \in U} |f(x_{1})-f(x_{2}| = 2 [/latex]. Budući da je supremum razlike jednak 2 za svaku takvu okolinu oko nule, tada je i infimum po tim okolinama jednak 2, tj. [latex]inf_{ \{U: 0 \in U otv. \} } ( sup_{x_{1},x_{2} \in U} |f(x_{1})-f(x_{2}| )= 2 [/latex], a to je po definiciji oscilacija u nuli.
U svim točkama osim nule funkcija signum (ta je bila zadana) je neprekidna pa je oscilacija nula. Sad promatramo okoline od nule. Svaka takva okolina sadrži barem jedan negativan i jedan pozitivan broj, tj. funkcija signum postiže vrijednosti -1,0,1 na takvoj okolini, pa je 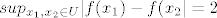 . Budući da je supremum razlike jednak 2 za svaku takvu okolinu oko nule, tada je i infimum po tim okolinama jednak 2, tj. 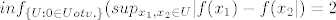 , a to je po definiciji oscilacija u nuli.
_________________
Rafael Mrđen
|
|
| [Vrh] |
|
kika
Forumaš(ica)
Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)
Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol:
Lokacija: Zagreb
|
|
| [Vrh] |
|
kika
Forumaš(ica)
Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
|
| [Vrh] |
|
ma
Forumaš(ica)
Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol:
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
napraviculom
Forumaš(ica)
Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol:
Lokacija: Scranton
|
| Postano: 10:40 sri, 23. 4. 2008 Naslov: |
|
|
|
moze li to malo konkretnije, npr. na primjeru iz poglavlja Fubinijev TM f:[0,1]x[0,2]-->|R, f(x,y)=y
moze li to malo konkretnije, npr. na primjeru iz poglavlja Fubinijev TM f:[0,1]x[0,2]→|R, f(x,y)=y
_________________
"I'm the operator with my pocket calculator"
|
|
| [Vrh] |
|
ma
Forumaš(ica)
Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol:
|
|
| [Vrh] |
|
ma
Forumaš(ica)
Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol:
|
| Postano: 11:41 sri, 23. 4. 2008 Naslov: |
|
|
|
[quote="napraviculom"]moze li to malo konkretnije, npr. na primjeru iz poglavlja Fubinijev TM f:[0,1]x[0,2]-->|R, f(x,y)=y[/quote]
kao što je Luuka rekao, gledaj samo ekvidistantne subdivizije i raspiši definicije gornje/donje darbouxove sume. imaš infimume i supremume na malim pravokutnicima čije površine izrazi pomoću razmaka na subdiviziji x i y osi. samo puno raspisivanja. i onda dobiješ izraze za s(P) i S(P), ovisne o m i/ili n, naravno. zapravo dobiješ dva skupa (skupove donjih i gornjih d-suma) i gladaš njihov supremum, odnosno infimum. trebaju biti jednaki.
| napraviculom (napisa): | | moze li to malo konkretnije, npr. na primjeru iz poglavlja Fubinijev TM f:[0,1]x[0,2]→|R, f(x,y)=y |
kao što je Luuka rekao, gledaj samo ekvidistantne subdivizije i raspiši definicije gornje/donje darbouxove sume. imaš infimume i supremume na malim pravokutnicima čije površine izrazi pomoću razmaka na subdiviziji x i y osi. samo puno raspisivanja. i onda dobiješ izraze za s(P) i S(P), ovisne o m i/ili n, naravno. zapravo dobiješ dva skupa (skupove donjih i gornjih d-suma) i gladaš njihov supremum, odnosno infimum. trebaju biti jednaki.
_________________
ima let u finish
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
ma
Forumaš(ica)
Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol:
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
|
(mislim na to da je supremum donjih (infimum gornjih) d-suma po ekvidistantnim subdivizijama danog pravokutnika zapravo jednak supremumu donjih (infimumu gornjih) d-suma po svim subdivizijama)
