| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
kaj
Forumaš(ica)
Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
 Postano: 13:28 pon, 5. 4. 2010 Naslov: |
    |
|
|
[quote="pajopatak"]Sada kad određujem djelovanje,ove brojeve koje dobijem: 1,1,-1,8,0,-5 kamo to ubacujem,umjesto a,b,c,d,e,f ilil? Neznam kako si ti dobio ovih -825[/quote]
Aha, ovo tvoje je prikaz linearnog funkcionala pomoću elemenata dualne baze. Ja sam dobio ovih -825 tako da sam ubacio matricu B u alfa1, tj,
uvrstio sam a=1, b=-1....to je ovo tzv. djelovanje.
| pajopatak (napisa): | | Sada kad određujem djelovanje,ove brojeve koje dobijem: 1,1,-1,8,0,-5 kamo to ubacujem,umjesto a,b,c,d,e,f ilil? Neznam kako si ti dobio ovih -825 |
Aha, ovo tvoje je prikaz linearnog funkcionala pomoću elemenata dualne baze. Ja sam dobio ovih -825 tako da sam ubacio matricu B u alfa1, tj,
uvrstio sam a=1, b=-1....to je ovo tzv. djelovanje.
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)
Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
kaj
Forumaš(ica)
Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)
Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
| Postano: 14:00 pon, 5. 4. 2010 Naslov: |
|
|
|
Ovako, ja ću pokušati riješiti ovaj zadatak, mislim da je ovako dosta zbunjujuće :D
Znači, označimo elemente baze sa [latex]f_{1},...,f_{6}.[/latex]
Prikažemo sad proizvoljnu matricu A u toj bazi, matrica je naravno u prikazu [latex]A=\begin{bmatrix} a & b \\ c & d \\ e & f \end{bmatrix}[/latex]:
[latex]A=\alpha f_{1}+\beta f_{2} + \gamma f_{3} + \delta f_{4} + \epsilon f_{5} + \omega f_{6}[/latex]
Računanjem ćemo dobiti pripadne koeficijente koji su upravo djelovanje elemenata baze na matricu A:
[latex]\alpha=f_{1}^{*}(A)=a-2b+6c-24d+120e-720f
\\
\\ \beta=f_{2}^{*}(A)=b-3c+12d-60e+360f
\\
\\ \gamma=f_{3}^{*}(A)=c-4d+20e-120f
\\
\\ \delta=f_{4}^{*}(A)=d-5e+30f
\\
\\ \epsilon=f_{5}^{*}(A)=e-6f
\\
\\ \omega=f_{6}^{*}(A)=f
[/latex]
Dualna baza je sada naravno [latex]\{f_{1}^{*},{f_{2}^{*},{f_{3}^{*},{f_{4}^{*},{f_{5}^{*},{f_{6}^{*}\},[/latex]
Kao što smo rekli, djelovanje na B ćemo dobiti ako uvrstimo B umjesto A kod djelovanja elemenata baze, dobije se:
[latex]f_{1}^{*}(B)=-825,\ ...\ f_{6}^{*}(B)=1[/latex]
I napokon, prikaz operatora u dualnoj bazi jest:
[latex]
f^{*}=Af_{1}^{*}+Bf_{2}^{*}+Cf_{3}^{*}+Df_{4}^{*}+Ef_{5}^{*}+Gf_{6}^{*}[/latex]
Djelujemo li sa elementima baze dobivamo upravo koeficijente A,...,F koji nam trebaju:
[latex]f^{*}(f_{1})=1=A, f^{*}(f_{2})=1=B, C=-1, D=8, E=-1, F=-5.[/latex]
pa je prikaz operatora i dualnoj bazi:
[latex]f^{*}=f_{1}^{*}+f_{2}^{*}-f_{3}^{*}+8f_{4}^{*}-f_{5}^{*}-5f_{6}^{*}[/latex]
Nadam se da nisam neku glupost napisao :D
Ovako, ja ću pokušati riješiti ovaj zadatak, mislim da je ovako dosta zbunjujuće 
Znači, označimo elemente baze sa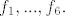 
Prikažemo sad proizvoljnu matricu A u toj bazi, matrica je naravno u prikazu  :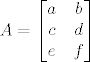
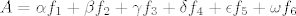
Računanjem ćemo dobiti pripadne koeficijente koji su upravo djelovanje elemenata baze na matricu A:
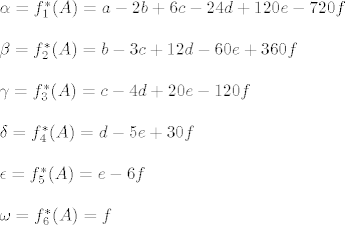
Dualna baza je sada naravno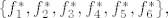 
Kao što smo rekli, djelovanje na B ćemo dobiti ako uvrstimo B umjesto A kod djelovanja elemenata baze, dobije se:
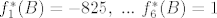
I napokon, prikaz operatora u dualnoj bazi jest:
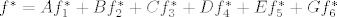
Djelujemo li sa elementima baze dobivamo upravo koeficijente A,...,F koji nam trebaju:
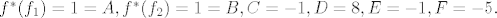
pa je prikaz operatora i dualnoj bazi:
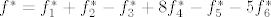
Nadam se da nisam neku glupost napisao
Zadnja promjena: Genaro; 16:11 pon, 5. 4. 2010; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)
Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)
Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol:
Lokacija: Zagreb
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)
Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
| Postano: 14:31 pon, 5. 4. 2010 Naslov: |
|
|
|
[quote="Genaro"]Mislim da je dokaz praktički isti kao onaj u propoziciji 1.4.10 na str 18/19 u prof Bakićevoj skripti, e sad da li ga potpuno razumijem, to je drugo pitanje :D[/quote]
Da,to je odgovor,ali za godinu 2009.ja sam mislila na onaj kolokvij u kojem smo rješavali onaj 4.zd iz 2008.
Pitanje: V kondim.,A je singularan na V.Dokaži da postoji B!=0 na V t.d je BA=0.
| Genaro (napisa): | | Mislim da je dokaz praktički isti kao onaj u propoziciji 1.4.10 na str 18/19 u prof Bakićevoj skripti, e sad da li ga potpuno razumijem, to je drugo pitanje |
Da,to je odgovor,ali za godinu 2009.ja sam mislila na onaj kolokvij u kojem smo rješavali onaj 4.zd iz 2008.
Pitanje: V kondim.,A je singularan na V.Dokaži da postoji B!=0 na V t.d je BA=0.
|
|
| [Vrh] |
|
kaj
Forumaš(ica)
Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
| Postano: 14:46 pon, 5. 4. 2010 Naslov: |
|
|
|
Ako je A singularan tada postoje neki vektori različiti od nule koje A šalje u nulu, odnosno jezgra mu nije trivijalna. Sada B definiramo tako da one vektore koje A ne šalje u nulu, B njihove slike šalje u nulu. Oni vektori koje A šalje u nulu , njih će B ionako slati u nulu jer je linearan.Sada vrijedi BA=0. Eto, tak bi ja riješio, al mislim da smo nešto slično imali u prvoj DZ... :)
Ako je A singularan tada postoje neki vektori različiti od nule koje A šalje u nulu, odnosno jezgra mu nije trivijalna. Sada B definiramo tako da one vektore koje A ne šalje u nulu, B njihove slike šalje u nulu. Oni vektori koje A šalje u nulu , njih će B ionako slati u nulu jer je linearan.Sada vrijedi BA=0. Eto, tak bi ja riješio, al mislim da smo nešto slično imali u prvoj DZ... 
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)
Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
smajl
Forumaš(ica)
Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
| Postano: 15:33 pon, 5. 4. 2010 Naslov: |
|
|
|
[quote="Genaro"]Ovako, ja ću pokušati riješiti ovaj zadatak, mislim da je ovako dosta zbunjujuće :D
Znači, označimo elemente baze sa [latex]f_{1},...,f_{6}.[/latex]
Prikažemo sad proizvoljnu matricu A u toj bazi, matrica je naravno u prikazu [latex]A=\begin{bmatrix} a & b \\ c & d \\ e & f \end{bmatrix}[/latex]:
[latex]A=\alpha f_{1}+\beta f_{2} + \gamma f_{3} + \delta f_{4} + \epsilon f_{5} + \omega f_{6}[/latex]
Računanjem ćemo dobiti pripadne koeficijente koji su upravo djelovanje elemenata baze na matricu A:
[latex]\alpha=f_{1}^{*}(A)=a-2b+6c-24d+120e-720f
\\
\\ \beta=f_{2}^{*}(A)=b-3c+12d-60e+360f
\\
\\ \gamma=f_{3}^{*}(A)=c-4d+20e-120f
\\
\\ \delta=f_{4}^{*}(A)=d-5e+30f
\\
\\ \epsilon=f_{5}^{*}(A)=e-6f
\\
\\ \omega=f_{6}(A)=f
[/latex]
Dualna baza je sada naravno [latex]\{f_{1}^{*},{f_{2}^{*},{f_{3}^{*},{f_{4}^{*},{f_{5}^{*},{f_{6}^{*}\},[/latex]
Kao što smo rekli, djelovanje na B ćemo dobiti ako uvrstimo B umjesto A kod djelovanja elemenata baze, dobije se:
[latex]f_{1}^{*}(B)=-825,\ ...\ f_{6}^{*}(B)=1[/latex]
I napokon, prikaz operatora u dualnoj bazi jest:
[latex]
f^{*}=Af_{1}^{*}+Bf_{2}^{*}+Cf_{3}^{*}+Df_{4}^{*}+Ef_{5}^{*}+Gf_{6}^{*}[/latex]
Djelujemo li sa elementima baze dobivamo upravo koeficijente A,...,F koji nam trebaju:
[latex]f^{*}(f_{1})=1=A, f^{*}(f_{2})=1=B, C=-1, D=8, E=0, F=-5.[/latex]
pa je prikaz operatora i dualnoj bazi:
[latex]f^{*}=f_{1}^{*}+f_{2}^{*}-f_{3}^{*}+8f_{4}^{*}-5f_{6}^{*}[/latex]
Nadam se da nisam neku glupost napisao :D[/quote]
Kako si dobio da je E=0? Ja bi rekla da je -1? Ili sam ja mozda negdje fulala u racunu :?
| Genaro (napisa): | Ovako, ja ću pokušati riješiti ovaj zadatak, mislim da je ovako dosta zbunjujuće
Znači, označimo elemente baze sa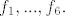
Prikažemo sad proizvoljnu matricu A u toj bazi, matrica je naravno u prikazu :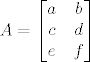
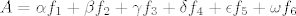
Računanjem ćemo dobiti pripadne koeficijente koji su upravo djelovanje elemenata baze na matricu A:
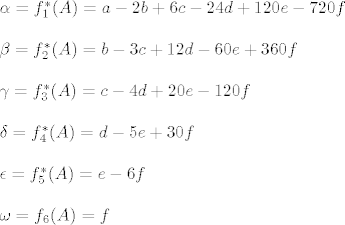
Dualna baza je sada naravno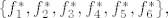
Kao što smo rekli, djelovanje na B ćemo dobiti ako uvrstimo B umjesto A kod djelovanja elemenata baze, dobije se:
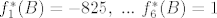
I napokon, prikaz operatora u dualnoj bazi jest:
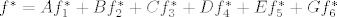
Djelujemo li sa elementima baze dobivamo upravo koeficijente A,...,F koji nam trebaju:
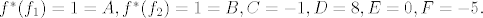
pa je prikaz operatora i dualnoj bazi:
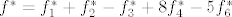
Nadam se da nisam neku glupost napisao |
Kako si dobio da je E=0? Ja bi rekla da je -1? Ili sam ja mozda negdje fulala u racunu 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)
Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol:
Lokacija: Zagreb
|
|
| [Vrh] |
|
smajl
Forumaš(ica)
Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol:
Lokacija: Zagreb
|
|
| [Vrh] |
|
dina12
Forumaš(ica)
Pridružen/a: 21. 11. 2009. (17:20:26)
Postovi: (18)16
|
|
| [Vrh] |
|
smajl
Forumaš(ica)
Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol:
Lokacija: Zagreb
|
|
| [Vrh] |
|
kaj
Forumaš(ica)
Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
kikyca
Forumaš(ica)
Pridružen/a: 13. 10. 2009. (18:45:07)
Postovi: (32)16
Spol:
|
|
| [Vrh] |
|
kaj
Forumaš(ica)
Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)
Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol:
|
|
| [Vrh] |
|
kikyca
Forumaš(ica)
Pridružen/a: 13. 10. 2009. (18:45:07)
Postovi: (32)16
Spol:
|
|
| [Vrh] |
|
minora665
Forumaš(ica)
Pridružen/a: 10. 02. 2010. (22:52:01)
Postovi: (1F)16
|
|
| [Vrh] |
|
|
Znači onaj prikaz mi je isto dobar s tim koeficjentima?
jeste dokazali ovo u 5.zd
