| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 22:39 pon, 10. 1. 2011 Naslov: Postano: 22:39 pon, 10. 1. 2011 Naslov: |
    |
|
|
[quote="kikzmyster"]Moze i 25. zadatak, ako nije problem?[/quote]
Neka je [latex]g(x) = f(x+1)-f(x)[/latex] za [latex]x\in \[0,1\][/latex]. Nadalje neka je [latex]f(0) = a[/latex] i [latex]f(2)=b[/latex]. Treba dakle dokazati da postoji [latex]x\in \[0,1\][/latex] za koji je [latex]g(x)=\frac{b-a}2[/latex]. Neka je dalje [latex]f(1)=c[/latex]. Sada je [latex]g(0) = c-a[/latex] i [latex]g(1)=b-c[/latex]. Prosjek od [latex]g(0)[/latex] i [latex]g(1)[/latex] iznosi [latex]\frac{b-a}2[/latex]. Dakle slika od [latex]g[/latex], budući da je to neprekidna funkcija, je segment koji uključuje [latex]g(0)[/latex] i [latex]g(1)[/latex], pa onda uključuje i njihov prosjek, i time smo gotovi.
| kikzmyster (napisa): | | Moze i 25. zadatak, ako nije problem? |
Neka je 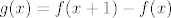 za za  . Nadalje neka je . Nadalje neka je 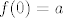 i i 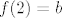 . Treba dakle dokazati da postoji . Treba dakle dokazati da postoji  za koji je za koji je 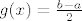 . Neka je dalje . Neka je dalje 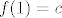 . Sada je . Sada je 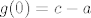 i i 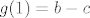 . Prosjek od . Prosjek od 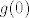 i i 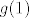 iznosi iznosi 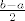 . Dakle slika od . Dakle slika od  , budući da je to neprekidna funkcija, je segment koji uključuje , budući da je to neprekidna funkcija, je segment koji uključuje 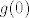 i i 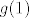 , pa onda uključuje i njihov prosjek, i time smo gotovi. , pa onda uključuje i njihov prosjek, i time smo gotovi.
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
 Postano: 23:04 pon, 10. 1. 2011 Naslov: Postano: 23:04 pon, 10. 1. 2011 Naslov: |
    |
|
|
E hvala...
I jos samo ovo.. zanima me kod zadataka kao 28., kako se dokazuje da smo nasli bas sve takve funkcije? Npr. bas u 28., f(x) = ax+b prvo pada na pamet, ali kako bi (konkretno u ovom zadatku) trazio daljnja rjesenja, ako ih ima, i (opcenito) kako bi dokazao da su to jedina rjesenja?
E hvala...
I jos samo ovo.. zanima me kod zadataka kao 28., kako se dokazuje da smo nasli bas sve takve funkcije? Npr. bas u 28., f(x) = ax+b prvo pada na pamet, ali kako bi (konkretno u ovom zadatku) trazio daljnja rjesenja, ako ih ima, i (opcenito) kako bi dokazao da su to jedina rjesenja?
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 23:21 pon, 10. 1. 2011 Naslov: Postano: 23:21 pon, 10. 1. 2011 Naslov: |
    |
|
|
Pa isto kao kad rješavaš jednadžbu: kad pogodiš rješenje, ti si našao jedno, ali nemaš pojma kako bi dokazao da nema drugih osim ako baš ne ideš rješavati jednadžbu. Isto je i s funkcijama: ako ja nizom implikacija pokažem da ako funkcija zadovoljava jednadžbu, onda je to linearna funkcija - time sam gotov, jer onda nema drugih. Dakle, treba krenuti od jednadžbe, a ne od rješenja.
Što se tiče 28., ja sam ovako razmišljao. Neka je [latex]f(0) = a[/latex] i [latex]f(1) = b[/latex]. Slutim da će cijeli graf biti pravac koji određuju te točke [latex](0,a)[/latex] i [latex](1,b)[/latex]. Sada koristeći jednadžbu izračunavam [latex]f(0.5)[/latex], [latex]f(0.25)[/latex], a također i [latex]f(2), f(4), f(3), f(0.75)[/latex]... Dokle to ide? Do svih realnih brojeva koji imaju konačan binarni zapis - jer krećem od vrijednosti za [latex]0[/latex] i [latex]1[/latex], te ako znam vrijednosti za [latex]x[/latex] i [latex]y[/latex], mogu saznati vrijednost za [latex]\frac{x+y}2[/latex] i slično, formalni dokaz toga ostavljam za vježbu a i napisat ću ako bude potrebno. Imamo dakle da za sve konačno zapisane binarne brojeve njihove funkcijske vrijednosti "leže na našem pravcu". Sad za neki broj [latex]x[/latex] s beskonačnim binarnim zapisom uzmemo niz brojeva s konačnim binarnim zapisom koji teži u [latex]x[/latex]. Sad zbog neprekidnosti, [latex]f(x)[/latex] je limes njihovih funkcijskih vrijednosti, i lako se dobije da je i on također na pravcu. Nisam bio formalan, ali mogu dopisati ako treba.
Pa isto kao kad rješavaš jednadžbu: kad pogodiš rješenje, ti si našao jedno, ali nemaš pojma kako bi dokazao da nema drugih osim ako baš ne ideš rješavati jednadžbu. Isto je i s funkcijama: ako ja nizom implikacija pokažem da ako funkcija zadovoljava jednadžbu, onda je to linearna funkcija - time sam gotov, jer onda nema drugih. Dakle, treba krenuti od jednadžbe, a ne od rješenja.
Što se tiče 28., ja sam ovako razmišljao. Neka je 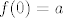 i i 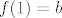 . Slutim da će cijeli graf biti pravac koji određuju te točke . Slutim da će cijeli graf biti pravac koji određuju te točke 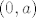 i i 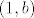 . Sada koristeći jednadžbu izračunavam . Sada koristeći jednadžbu izračunavam 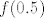 , , 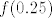 , a također i , a također i 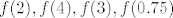 ... Dokle to ide? Do svih realnih brojeva koji imaju konačan binarni zapis - jer krećem od vrijednosti za ... Dokle to ide? Do svih realnih brojeva koji imaju konačan binarni zapis - jer krećem od vrijednosti za  i i  , te ako znam vrijednosti za , te ako znam vrijednosti za  i i  , mogu saznati vrijednost za , mogu saznati vrijednost za 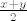 i slično, formalni dokaz toga ostavljam za vježbu a i napisat ću ako bude potrebno. Imamo dakle da za sve konačno zapisane binarne brojeve njihove funkcijske vrijednosti "leže na našem pravcu". Sad za neki broj i slično, formalni dokaz toga ostavljam za vježbu a i napisat ću ako bude potrebno. Imamo dakle da za sve konačno zapisane binarne brojeve njihove funkcijske vrijednosti "leže na našem pravcu". Sad za neki broj  s beskonačnim binarnim zapisom uzmemo niz brojeva s konačnim binarnim zapisom koji teži u s beskonačnim binarnim zapisom uzmemo niz brojeva s konačnim binarnim zapisom koji teži u  . Sad zbog neprekidnosti, . Sad zbog neprekidnosti, 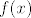 je limes njihovih funkcijskih vrijednosti, i lako se dobije da je i on također na pravcu. Nisam bio formalan, ali mogu dopisati ako treba. je limes njihovih funkcijskih vrijednosti, i lako se dobije da je i on također na pravcu. Nisam bio formalan, ali mogu dopisati ako treba.
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 10:25 uto, 11. 1. 2011 Naslov: Postano: 10:25 uto, 11. 1. 2011 Naslov: |
    |
|
|
Neka je [latex]kx+l[/latex] pravac koji prolazi tim točkama. U startu onda imamo da je [latex]f(0) = k\cdot 0 + l[/latex] kao i [latex]f(1) = k\cdot 1 + l[/latex].
Prvo indukcijom dokazujemo da funkcijske vrijednosti svih prirodnih brojeva "leže na tom pravcu", tj. da vrijedi [latex]f(n) = kn+l[/latex] za svaki [latex]n[/latex]. Baza nam je za [latex]0[/latex] i [latex]1[/latex]. Korak: neka je [latex]f(n) = kn+l[/latex] i [latex]f(n+1) = k(n+1)+l[/latex] za neki [latex]n[/latex]. Uvrstimo u jednadžbu [latex]x=n, y=n+2[/latex], pa dobijemo[latex] f(n+1) = \frac{f(n) + f(n+2)}2[/latex], i iz toga slijedi [latex]f(n+2) = 2f(n+1)-f(n) = k(n+2)+l[/latex], dakle ako tvrdnja vrijedi za [latex]n[/latex] i [latex]n+1[/latex], onda vrijedi i za [latex]n+2[/latex], indukcija gotova.
Dalje dokazujemo istu stvar za negativne cijele brojeve. Uvrštavanjem [latex]x=-n, y=n[/latex] dobivamo [latex]f(0) = \frac{f(-n)+f(n)}2[/latex] pa onda [latex]f(-n) = 2f(0)-f(n) =
k(-n)+l[/latex].
Sad tvrdim da je [latex]f(x) = kx+l[/latex] za svaki realni broj [latex]x[/latex] s konačnim binarnim zapisom. To dokazujem indukcijom po broju njegovih binarnih znamenaka iza decimalne točke. Baza: ako ima [latex]0[/latex] znamenaka iza točke onda je to cijeli broj, a za njih smo već dokazali. Korak: neka tvrdnja vrijedi za binarne brojeve s [latex]n[/latex] binarnih znamenaka iza točke. Uzmimo broj [latex]p[/latex] koji ima [latex]n+1[/latex] binarnih znamenaka iza točke. Uvrstimo [latex]x=0, y=2p[/latex]. Dobijemo [latex]f(p) = \frac{f(0)+f(2p)}2 = \frac{k\cdot 0 + l + k\cdot(2p) + l}2 = kp+l[/latex]. Pritom sam koristio [latex]f(2p) =k\cdot(2p)+l[/latex] jer to znam po pretpostavci indukcije (množenjem s 2 se smanjuje broj binarnih znamenaka iza točke). Gotovo!
Neka je 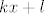 pravac koji prolazi tim točkama. U startu onda imamo da je pravac koji prolazi tim točkama. U startu onda imamo da je 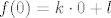 kao i kao i 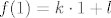 . .
Prvo indukcijom dokazujemo da funkcijske vrijednosti svih prirodnih brojeva "leže na tom pravcu", tj. da vrijedi 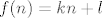 za svaki za svaki  . Baza nam je za . Baza nam je za  i i  . Korak: neka je . Korak: neka je 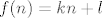 i i 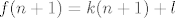 za neki za neki  . Uvrstimo u jednadžbu . Uvrstimo u jednadžbu 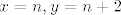 , pa dobijemo , pa dobijemo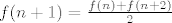 , i iz toga slijedi , i iz toga slijedi 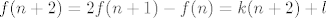 , dakle ako tvrdnja vrijedi za , dakle ako tvrdnja vrijedi za  i i 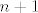 , onda vrijedi i za , onda vrijedi i za  , indukcija gotova. , indukcija gotova.
Dalje dokazujemo istu stvar za negativne cijele brojeve. Uvrštavanjem 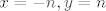 dobivamo dobivamo 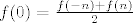 pa onda pa onda 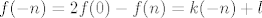 . .
Sad tvrdim da je 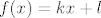 za svaki realni broj za svaki realni broj  s konačnim binarnim zapisom. To dokazujem indukcijom po broju njegovih binarnih znamenaka iza decimalne točke. Baza: ako ima s konačnim binarnim zapisom. To dokazujem indukcijom po broju njegovih binarnih znamenaka iza decimalne točke. Baza: ako ima  znamenaka iza točke onda je to cijeli broj, a za njih smo već dokazali. Korak: neka tvrdnja vrijedi za binarne brojeve s znamenaka iza točke onda je to cijeli broj, a za njih smo već dokazali. Korak: neka tvrdnja vrijedi za binarne brojeve s  binarnih znamenaka iza točke. Uzmimo broj binarnih znamenaka iza točke. Uzmimo broj  koji ima koji ima 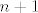 binarnih znamenaka iza točke. Uvrstimo binarnih znamenaka iza točke. Uvrstimo 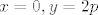 . Dobijemo . Dobijemo 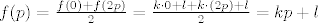 . Pritom sam koristio . Pritom sam koristio 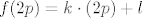 jer to znam po pretpostavci indukcije (množenjem s 2 se smanjuje broj binarnih znamenaka iza točke). Gotovo! jer to znam po pretpostavci indukcije (množenjem s 2 se smanjuje broj binarnih znamenaka iza točke). Gotovo!
|
|
| [Vrh] |
|
tiborr
Forumaš(ica)
Pridružen/a: 23. 12. 2012. (18:54:28)
Postovi: (E)16
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
|
| [Vrh] |
|
hendrix
Forumaš(ica)

Pridružen/a: 03. 09. 2012. (15:59:06)
Postovi: (92)16
|
 Postano: 1:48 ned, 6. 1. 2013 Naslov: Postano: 1:48 ned, 6. 1. 2013 Naslov: |
    |
|
|
Nisam uspio naci negdje na forumu pa molim neki hint za 14. a), zadatak se nalazi [url=http://web.math.pmf.unizg.hr/nastava/analiza/files/ma1-zadaca4.pdf]ovdje[/url].
edit: Uspio sam, mozda :D, izgurati nesto preko Teorema o sendvicu. Ako netko ima kakvu stvarno pametnu ideju, pitanje je i dalje otvoreno. :D
Nisam uspio naci negdje na forumu pa molim neki hint za 14. a), zadatak se nalazi ovdje.
edit: Uspio sam, mozda  , izgurati nesto preko Teorema o sendvicu. Ako netko ima kakvu stvarno pametnu ideju, pitanje je i dalje otvoreno. , izgurati nesto preko Teorema o sendvicu. Ako netko ima kakvu stvarno pametnu ideju, pitanje je i dalje otvoreno. 
Zadnja promjena: hendrix; 11:24 ned, 6. 1. 2013; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
|
| [Vrh] |
|
hendrix
Forumaš(ica)

Pridružen/a: 03. 09. 2012. (15:59:06)
Postovi: (92)16
|
|
| [Vrh] |
|
Shirohige
Forumaš(ica)

Pridružen/a: 16. 11. 2012. (20:19:56)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
hendrix
Forumaš(ica)

Pridružen/a: 03. 09. 2012. (15:59:06)
Postovi: (92)16
|
 Postano: 19:42 ned, 6. 1. 2013 Naslov: Postano: 19:42 ned, 6. 1. 2013 Naslov: |
    |
|
|
Pod a) raspisi sve po binomnom poucku, [tex]x-1[/tex] ce ti se skratiti, u brojniku ce ti ostati [tex]m[/tex], a u nazivniku [tex]n[/tex] pribrojnika koji ce svi ici u [tex]1[/tex] jer ce, osim prvog clana, koji je [tex]1[/tex], svi biti oblika [tex]1[/tex] "na nesto".
Pod b) trebas napraviti dvostruku racionalizaciju, pomnozi s jednim razlomkom (s jednakim brojnikom i nazivnikom, naravno) tako da nazivnik nastimas na razliku kubova, te potpuno istu stvar za brojnik (trebas mnoziti s [tex]\frac{1 - x^{1/5} + x^{2/5} - x^{3/5} + x^{4/5}}{1 - x^{1/5} + x^{2/5} - x^{3/5} + x^{4/5}}[/tex]), vjerujem da za kub znas nastimati, uostalom, analogno je. Do kraja je stvar cisto tehnicke prirode, skratis sto se da skratiti i odmah pustis limes.
Pod a) raspisi sve po binomnom poucku, [tex]x-1[/tex] ce ti se skratiti, u brojniku ce ti ostati [tex]m[/tex], a u nazivniku [tex]n[/tex] pribrojnika koji ce svi ici u [tex]1[/tex] jer ce, osim prvog clana, koji je [tex]1[/tex], svi biti oblika [tex]1[/tex] "na nesto".
Pod b) trebas napraviti dvostruku racionalizaciju, pomnozi s jednim razlomkom (s jednakim brojnikom i nazivnikom, naravno) tako da nazivnik nastimas na razliku kubova, te potpuno istu stvar za brojnik (trebas mnoziti s [tex]\frac{1 - x^{1/5} + x^{2/5} - x^{3/5} + x^{4/5}}{1 - x^{1/5} + x^{2/5} - x^{3/5} + x^{4/5}}[/tex]), vjerujem da za kub znas nastimati, uostalom, analogno je. Do kraja je stvar cisto tehnicke prirode, skratis sto se da skratiti i odmah pustis limes.
|
|
| [Vrh] |
|
Shirohige
Forumaš(ica)

Pridružen/a: 16. 11. 2012. (20:19:56)
Postovi: (ED)16
Spol: 
|
 Postano: 1:18 pon, 7. 1. 2013 Naslov: Postano: 1:18 pon, 7. 1. 2013 Naslov: |
    |
|
|
[quote="hendrix"]Pod a) raspisi sve po binomnom poucku, [tex]x-1[/tex] ce ti se skratiti, u brojniku ce ti ostati [tex]m[/tex], a u nazivniku [tex]n[/tex] pribrojnika koji ce svi ici u [tex]1[/tex] jer ce, osim prvog clana, koji je [tex]1[/tex], svi biti oblika [tex]1[/tex] "na nesto".
...[/quote]
Wolfram Alpha kaže da je dobro.
Evo jedna sarma! :D
| hendrix (napisa): | Pod a) raspisi sve po binomnom poucku, [tex]x-1[/tex] ce ti se skratiti, u brojniku ce ti ostati [tex]m[/tex], a u nazivniku [tex]n[/tex] pribrojnika koji ce svi ici u [tex]1[/tex] jer ce, osim prvog clana, koji je [tex]1[/tex], svi biti oblika [tex]1[/tex] "na nesto".
... |
Wolfram Alpha kaže da je dobro.
Evo jedna sarma! 
|
|
| [Vrh] |
|
|










