| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vinko
Forumaš(ica)

Pridružen/a: 26. 08. 2006. (23:08:00)
Postovi: (1A8)16
Spol: 
Lokacija: PMF-MO 214
|
|
| [Vrh] |
|
Meri
Forumaš(ica)

Pridružen/a: 11. 11. 2004. (14:48:32)
Postovi: (155)16
Spol: 
Lokacija: Zagreb, Zaaaaagreb...tararam...
|
|
| [Vrh] |
|
vinko
Forumaš(ica)

Pridružen/a: 26. 08. 2006. (23:08:00)
Postovi: (1A8)16
Spol: 
Lokacija: PMF-MO 214
|
 Postano: 1:33 uto, 10. 7. 2007 Naslov: Postano: 1:33 uto, 10. 7. 2007 Naslov: |
    |
|
|
[quote="Meri"]ahm....pitanje :)
59.strana, tm koji govori o rekurzijama za p' i q';
otkuda se vidi da je
p'(n-1) = a(n-1)*p'(n-2) + p'(n-3) i
q'(n-1) = a(n-1)*q'(n-2) + q'(n-3)?
hvala:)[/quote]
Dokaz ide indukcijom. Pretpostavili smo da tvrdnja vrijedi za n-1, pa stoga i za ver. razlomak [a1,a2, ..., a_{n-1},a_n]
| Meri (napisa): | ahm....pitanje 
59.strana, tm koji govori o rekurzijama za p' i q';
otkuda se vidi da je
p'(n-1) = a(n-1)*p'(n-2) + p'(n-3) i
q'(n-1) = a(n-1)*q'(n-2) + q'(n-3)?
hvala:) |
Dokaz ide indukcijom. Pretpostavili smo da tvrdnja vrijedi za n-1, pa stoga i za ver. razlomak [a1,a2, ..., a_{n-1},a_n]
|
|
| [Vrh] |
|
Meri
Forumaš(ica)

Pridružen/a: 11. 11. 2004. (14:48:32)
Postovi: (155)16
Spol: 
Lokacija: Zagreb, Zaaaaagreb...tararam...
|
|
| [Vrh] |
|
Glupko_3.14
Forumaš(ica)


Pridružen/a: 27. 09. 2007. (10:32:16)
Postovi: (77)16
|
|
| [Vrh] |
|
vinko
Forumaš(ica)

Pridružen/a: 26. 08. 2006. (23:08:00)
Postovi: (1A8)16
Spol: 
Lokacija: PMF-MO 214
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
|
| [Vrh] |
|
Glupko_3.14
Forumaš(ica)


Pridružen/a: 27. 09. 2007. (10:32:16)
Postovi: (77)16
|
|
| [Vrh] |
|
Glupko_3.14
Forumaš(ica)


Pridružen/a: 27. 09. 2007. (10:32:16)
Postovi: (77)16
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
|
| [Vrh] |
|
Glupko_3.14
Forumaš(ica)


Pridružen/a: 27. 09. 2007. (10:32:16)
Postovi: (77)16
|
|
| [Vrh] |
|
Glupko_3.14
Forumaš(ica)


Pridružen/a: 27. 09. 2007. (10:32:16)
Postovi: (77)16
|
 Postano: 18:59 ned, 30. 9. 2007 Naslov: Postano: 18:59 ned, 30. 9. 2007 Naslov: |
    |
|
|
u Teoremu 6.17. (Liuville) na str.71. u dokazu imamo:
[latex]|\sum_{i=1}^d{(\frac{p}{g}-\alpha)}^i \frac{1}{i!}P^{(i)}(\alpha)| < \frac{1}{c(\alpha)} |\alpha - \frac{p}{q}| [/latex], gdje je [latex]c(\alpha)=\frac{1}{2\sum_{i=1}^d\frac{1}{i!}|P^{(i)}(\alpha)|}[/latex],
kako smo dobili tu ocjenu?
vidim da mozemo izluciti [latex]|\alpha-\frac{p}{q}|[/latex] iz sume, i [latex]|\frac{p}{q}-\alpha| \leq 1[/latex] se valjda upotrijebi, ali ne znam kako tocno.
u Teoremu 6.17. (Liuville) na str.71. u dokazu imamo:
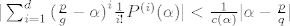 , gdje je , gdje je 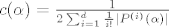 , ,
kako smo dobili tu ocjenu?
vidim da mozemo izluciti  iz sume, i iz sume, i 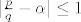 se valjda upotrijebi, ali ne znam kako tocno. se valjda upotrijebi, ali ne znam kako tocno.
_________________
Nov, još gluplji.
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
 Postano: 19:19 ned, 30. 9. 2007 Naslov: Postano: 19:19 ned, 30. 9. 2007 Naslov: |
    |
|
|
[quote="Glupko_3.14"]u Teoremu 6.17. (Liuville) na str.71. u dokazu imamo:
[latex]|\sum_{i=1}^d{(\frac{p}{g}-\alpha)}^i \frac{1}{i!}P^{(i)}(\alpha)| < \frac{1}{c(\alpha)} |\alpha - \frac{p}{q}| [/latex], gdje je [latex]c(\alpha)=\frac{1}{2\sum_{i=1}^d\frac{1}{i!}|P^{(i)}(\alpha)|}[/latex],
kako smo dobili tu ocjenu?
vidim da mozemo izluciti [latex]|\alpha-\frac{p}{q}|[/latex] iz sume, i [latex]|\frac{p}{q}-\alpha| \leq 1[/latex] se valjda upotrijebi, ali ne znam kako tocno.[/quote]
Osim izlucivanja [latex]|\alpha-\frac{p}{q}|[/latex] i pretpostavke [latex]|\frac{p}{q}-\alpha| \leq 1[/latex], koristi se jos nejednakost trokuta (apsolutna vrijednost sume <= suma apsolutnih vrijednosti) i nejednakost [latex]1 < 2[/latex].
| Glupko_3.14 (napisa): | u Teoremu 6.17. (Liuville) na str.71. u dokazu imamo:
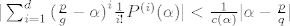 , gdje je , gdje je 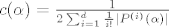 , ,
kako smo dobili tu ocjenu?
vidim da mozemo izluciti  iz sume, i iz sume, i 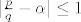 se valjda upotrijebi, ali ne znam kako tocno. se valjda upotrijebi, ali ne znam kako tocno. |
Osim izlucivanja  i pretpostavke i pretpostavke 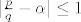 , koristi se jos nejednakost trokuta (apsolutna vrijednost sume ⇐ suma apsolutnih vrijednosti) i nejednakost , koristi se jos nejednakost trokuta (apsolutna vrijednost sume ⇐ suma apsolutnih vrijednosti) i nejednakost 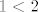 . .
|
|
| [Vrh] |
|
Glupko_3.14
Forumaš(ica)


Pridružen/a: 27. 09. 2007. (10:32:16)
Postovi: (77)16
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
|
| [Vrh] |
|
Glupko_3.14
Forumaš(ica)


Pridružen/a: 27. 09. 2007. (10:32:16)
Postovi: (77)16
|
 Postano: 21:51 ned, 30. 9. 2007 Naslov: Postano: 21:51 ned, 30. 9. 2007 Naslov: |
    |
|
|
hvala jos jednom.
dakle, ovakav je slijed zakljucivanja: iz Tm 6.16.imamo da minimalni polinom sigurno dijeli f, a jedini polinom stupnja manjeg od 2 (sto je onda 1) i ponistava alfa bi bio [latex]g(x)=x-\alpha[/latex], no on nema racionalne koeficijente posto [latex]\alpha[/latex] nije racionalan -> f je minimalni polinom koji ponistava alfa. (?)
[quote="duje"]
Pa vi ste dosli skoro do kraja skripte :shock: :D
[/quote]
mislite li da je to cudno s obzirom na moje intelektualne sposobnosti? :lol:
retoricko je pitanje, naravno :D
hvala jos jednom.
dakle, ovakav je slijed zakljucivanja: iz Tm 6.16.imamo da minimalni polinom sigurno dijeli f, a jedini polinom stupnja manjeg od 2 (sto je onda 1) i ponistava alfa bi bio 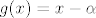 , no on nema racionalne koeficijente posto , no on nema racionalne koeficijente posto  nije racionalan → f je minimalni polinom koji ponistava alfa. (?) nije racionalan → f je minimalni polinom koji ponistava alfa. (?)
| duje (napisa): |
Pa vi ste dosli skoro do kraja skripte  
|
mislite li da je to cudno s obzirom na moje intelektualne sposobnosti? 
retoricko je pitanje, naravno 
_________________
Nov, još gluplji.
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
|
| [Vrh] |
|
|














