| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
blob
Forumaš(ica)


Pridružen/a: 13. 07. 2007. (18:09:52)
Postovi: (23)16
|
 Postano: 20:06 sri, 3. 10. 2007 Naslov: Dokaz da je f(A U B)=f(A) U f(B) Postano: 20:06 sri, 3. 10. 2007 Naslov: Dokaz da je f(A U B)=f(A) U f(B) |
    |
|
|
Znam da je pitanje sigurno trivijalno, ali nekome tko se s time susreće u prvom tjednu prve godine studija, još nenaviklom na matematičku strogoću i preciznost, ipak možda i nije tako bezazleno.
Kontekst je sljedeći: Neka je [latex]f:D\rightarrow K[/latex] funkcija i [latex]A,B\subseteq D[/latex]. Pokažite da vrijedi [latex]f(A \cup B)=f(A) \cup f(B)[/latex]. Srž dokaza mi je jasna; pokazano je da vrijedi [latex]y\in f(A \cup B) \Rightarrow y\in f(A) \cup f(B)[/latex]. Odnosno, riječima, ako je y element slike skupa [latex](A \cup B)[/latex] po funkciji [latex]f[/latex], onda je taj y ujedno i element barem jednog skupa [latex]f(A)[/latex], ili [latex]f(B)[/latex], ili oba.
Evo što me muči: iz navedenog
[latex]y\in f(A \cup B) \Rightarrow y\in f(A) \cup f(B)[/latex] slijedi zaključak
[latex]f(A \cup B) \subseteq f(A) \cup f(B)[/latex]. Iz čega točno proizlazi [latex]\subseteq[/latex]?
Jasno mi je, ako gornju priču ispričamo riječima i uzmemo da su [latex]A[/latex] i [latex]B[/latex] neka druga dva skupa, da ako postavimo implikaciju "Ako je x element skupa A, onda je x također i element skupa B, pri čemu tvrdnja vrijedi za sve x-eve iz A.", da je moguće da A bude podskup od B ili čak da mu bude ekvivalentan (dok B nikako ne može biti podskup od A, jer u tom slučaju bi postojali x-evi iz A koji se ne bi istovremeno nalazili u B). Zanima me kako možemo matematički precizno tvrditi da vrijedi [latex]A \subseteq B[/latex], koliko god da su te dvije mogućnosti ([latex]A=B[/latex] i [latex]A \subset B[/latex]) intuitivno jasne i očigledne?
Da si to razjasnim, krenuo sam crtkarati razna preslikavanja, poput ovog,
[URL=http://imageshack.us][img]http://img124.imageshack.us/img124/7003/skupovi001cropvn7.jpg[/img][/URL]
gdje sam se uvjerio da doista vrijedi [latex]f(A \cup B)=f(A) \cup f(B)[/latex], no nikako nisam došao do slučaja gdje bi vrijedilo [latex]f(A \cup B)\subset f(A) \cup f(B)[/latex]. Možete li mi dati primjer skup(ov)a gdje bi ta jednakost važila? Jer to je ključno za dokaz: treba prvo pokazati npr. [latex]K\subseteq L[/latex] i zatim [latex]L\subseteq K[/latex] i [b][i]tek onda[/i][/b] zaključiti da je [latex]K=L[/latex].
Znam da je pitanje sigurno trivijalno, ali nekome tko se s time susreće u prvom tjednu prve godine studija, još nenaviklom na matematičku strogoću i preciznost, ipak možda i nije tako bezazleno.
Kontekst je sljedeći: Neka je 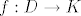 funkcija i funkcija i 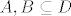 . Pokažite da vrijedi . Pokažite da vrijedi 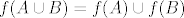 . Srž dokaza mi je jasna; pokazano je da vrijedi . Srž dokaza mi je jasna; pokazano je da vrijedi 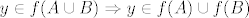 . Odnosno, riječima, ako je y element slike skupa . Odnosno, riječima, ako je y element slike skupa 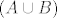 po funkciji po funkciji  , onda je taj y ujedno i element barem jednog skupa , onda je taj y ujedno i element barem jednog skupa 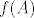 , ili , ili 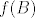 , ili oba. , ili oba.
Evo što me muči: iz navedenog
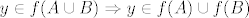 slijedi zaključak slijedi zaključak
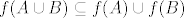 . Iz čega točno proizlazi . Iz čega točno proizlazi  ? ?
Jasno mi je, ako gornju priču ispričamo riječima i uzmemo da su  i i  neka druga dva skupa, da ako postavimo implikaciju "Ako je x element skupa A, onda je x također i element skupa B, pri čemu tvrdnja vrijedi za sve x-eve iz A.", da je moguće da A bude podskup od B ili čak da mu bude ekvivalentan (dok B nikako ne može biti podskup od A, jer u tom slučaju bi postojali x-evi iz A koji se ne bi istovremeno nalazili u B). Zanima me kako možemo matematički precizno tvrditi da vrijedi neka druga dva skupa, da ako postavimo implikaciju "Ako je x element skupa A, onda je x također i element skupa B, pri čemu tvrdnja vrijedi za sve x-eve iz A.", da je moguće da A bude podskup od B ili čak da mu bude ekvivalentan (dok B nikako ne može biti podskup od A, jer u tom slučaju bi postojali x-evi iz A koji se ne bi istovremeno nalazili u B). Zanima me kako možemo matematički precizno tvrditi da vrijedi 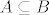 , koliko god da su te dvije mogućnosti ( , koliko god da su te dvije mogućnosti (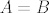 i i 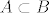 ) intuitivno jasne i očigledne? ) intuitivno jasne i očigledne?
Da si to razjasnim, krenuo sam crtkarati razna preslikavanja, poput ovog,

gdje sam se uvjerio da doista vrijedi 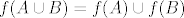 , no nikako nisam došao do slučaja gdje bi vrijedilo , no nikako nisam došao do slučaja gdje bi vrijedilo 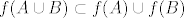 . Možete li mi dati primjer skup(ov)a gdje bi ta jednakost važila? Jer to je ključno za dokaz: treba prvo pokazati npr. . Možete li mi dati primjer skup(ov)a gdje bi ta jednakost važila? Jer to je ključno za dokaz: treba prvo pokazati npr.  i zatim i zatim 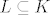 i tek onda zaključiti da je i tek onda zaključiti da je 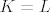 . .
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 20:16 sri, 3. 10. 2007 Naslov: Postano: 20:16 sri, 3. 10. 2007 Naslov: |
    |
|
|
Ako je [latex]y \in f(A) \cup f(B)[/latex], onda je [latex]y \in f(A)[/latex] ili [latex]y \in f(B)[/latex]. :) U prvom slucaju:
[latex]\exists x \in A:\ y = f(x)[/latex].
U drugom, analogno:
[latex]\exists x \in B:\ y = f(x)[/latex]
Ukupno:
[latex]\exists x \in A \cup B:\ y = f(x)[/latex],
tj.
[latex]y \in f(A \cup B)[/latex]
8)
Ako je 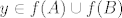 , onda je , onda je 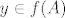 ili ili 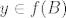 . .  U prvom slucaju: U prvom slucaju:
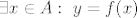 . .
U drugom, analogno:
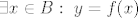
Ukupno:
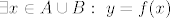 , ,
tj.
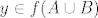

_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
ß
Forumaš(ica)
Pridružen/a: 29. 07. 2006. (15:29:06)
Postovi: (115)16
Spol: 
Lokacija: Graveyard Mountain Home
|
 Postano: 20:28 sri, 3. 10. 2007 Naslov: Re: Dokaz da je f(A U B)=f(A) U f(B) Postano: 20:28 sri, 3. 10. 2007 Naslov: Re: Dokaz da je f(A U B)=f(A) U f(B) |
    |
|
|
[quote="blob"]Evo što me muči: iz navedenog
[latex]y\in f(A \cup B) \Rightarrow y\in f(A) \cup f(B)[/latex] slijedi zaključak
[latex]f(A \cup B) \subseteq f(A) \cup f(B)[/latex]. Iz čega točno proizlazi [latex]\subseteq[/latex]?[/quote]
Sorry ako sam te krivo shvatio, ali evo:
Ukoliko iz činjenice da je recimo [latex]y\in A[/latex] slijedi [latex]y\in B[/latex] (i ovo vrijedi za proizvoljni y), iz toga očito slijedi da je A podskup od B ( [latex]A\subseteq B[/latex]).
Zašto je to očito? Pa, iz same definicije podskupa (ukoliko je tako nešto uopće potrebno definirati) -> A je podskup od B ako je svaki član od A ujedno i član od B, i to je to.
U tvom gornjem primjeru samo zamijeni moje A i B sa odgovarajućim izrazima (za sliku unije odnosno uniju slika), i to je upravo ono što si napisao.
E, sad:
[quote="blob"] no nikako nisam došao do slučaja gdje bi vrijedilo [latex]f(A \cup B)\subset f(A) \cup f(B)[/latex]. Možete li mi dati primjer skup(ov)a gdje bi ta jednakost važila? Jer to je ključno za dokaz: treba prvo pokazati npr. [latex]K\subseteq L[/latex] i zatim [latex]L\subseteq K[/latex] i [b][i]tek onda[/i][/b] zaključiti da je [latex]K=L[/latex].[/quote]
Mislim da bi problem mogao biti u krivom shvaćanju simbola [latex]\subset[/latex].
Ovaj simbol, koliko ja znam, znači [b]pravi podskup[/b], odnosno podskup koji nije jednak "originalnom" skupu. [i]To je poseban slučaj podskupa, a ne obrnuto[/i], da se tako izrazim. :)
Dakle, vrijedi [latex]A \subseteq A[/latex], ali ne može vrijediti [latex]A \subset A[/latex].
Za ovu jednakost: [latex]f(A \cup B)\subset f(A) \cup f(B)[/latex] ne mogu ti dati primjer, jer primjer ne postoji. Ukoliko su dva skupa jednaka, među njima ne može postojati odnos pravog podskupa, nego samo podskupa.
Ako nisi pogrešno shvatio odnos simbola [latex]\subset[/latex] i [latex]\subseteq[/latex] (odnosno onog što oni predstavljaju), onda se ispričavam, i u tom slučaju ti je vjerojatno ovaj post beskoristan. :?
| blob (napisa): | Evo što me muči: iz navedenog
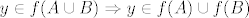 slijedi zaključak slijedi zaključak
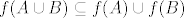 . Iz čega točno proizlazi . Iz čega točno proizlazi  ? ? |
Sorry ako sam te krivo shvatio, ali evo:
Ukoliko iz činjenice da je recimo 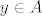 slijedi slijedi 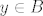 (i ovo vrijedi za proizvoljni y), iz toga očito slijedi da je A podskup od B ( (i ovo vrijedi za proizvoljni y), iz toga očito slijedi da je A podskup od B ( 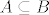 ). ).
Zašto je to očito? Pa, iz same definicije podskupa (ukoliko je tako nešto uopće potrebno definirati) → A je podskup od B ako je svaki član od A ujedno i član od B, i to je to.
U tvom gornjem primjeru samo zamijeni moje A i B sa odgovarajućim izrazima (za sliku unije odnosno uniju slika), i to je upravo ono što si napisao.
E, sad:
| blob (napisa): | no nikako nisam došao do slučaja gdje bi vrijedilo 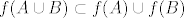 . Možete li mi dati primjer skup(ov)a gdje bi ta jednakost važila? Jer to je ključno za dokaz: treba prvo pokazati npr. . Možete li mi dati primjer skup(ov)a gdje bi ta jednakost važila? Jer to je ključno za dokaz: treba prvo pokazati npr.  i zatim i zatim 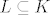 i tek onda zaključiti da je i tek onda zaključiti da je 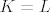 . . |
Mislim da bi problem mogao biti u krivom shvaćanju simbola 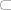 . .
Ovaj simbol, koliko ja znam, znači pravi podskup, odnosno podskup koji nije jednak "originalnom" skupu. To je poseban slučaj podskupa, a ne obrnuto, da se tako izrazim. 
Dakle, vrijedi 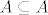 , ali ne može vrijediti , ali ne može vrijediti 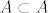 . .
Za ovu jednakost: 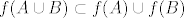 ne mogu ti dati primjer, jer primjer ne postoji. Ukoliko su dva skupa jednaka, među njima ne može postojati odnos pravog podskupa, nego samo podskupa. ne mogu ti dati primjer, jer primjer ne postoji. Ukoliko su dva skupa jednaka, među njima ne može postojati odnos pravog podskupa, nego samo podskupa.
Ako nisi pogrešno shvatio odnos simbola 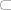 i i  (odnosno onog što oni predstavljaju), onda se ispričavam, i u tom slučaju ti je vjerojatno ovaj post beskoristan. (odnosno onog što oni predstavljaju), onda se ispričavam, i u tom slučaju ti je vjerojatno ovaj post beskoristan. 
_________________
Devious movements in your eyes moved me from relief
Breath comes out white clouds with your lies
and filters through me
|
|
| [Vrh] |
|
ß
Forumaš(ica)

Pridružen/a: 29. 07. 2006. (15:29:06)
Postovi: (115)16
Spol: 
Lokacija: Graveyard Mountain Home
|
 Postano: 20:43 sri, 3. 10. 2007 Naslov: Re: Dokaz da je f(A U B)=f(A) U f(B) Postano: 20:43 sri, 3. 10. 2007 Naslov: Re: Dokaz da je f(A U B)=f(A) U f(B) |
    |
|
|
[quote="blob"] Zanima me kako možemo matematički precizno tvrditi da vrijedi [latex]A \subseteq B[/latex], koliko god da su te dvije mogućnosti ([latex]A=B[/latex] i [latex]A \subset B[/latex]) intuitivno jasne i očigledne?[/quote]
Da, ovo nisam citirao u gornjem postu a cini mi se da je upravo tu odgovor:
[latex]A \subseteq B[/latex] [b]ne znaci[/b] isto sto i
[latex]A=B[/latex] [b]i[/b] [latex]A \subset B[/latex].
Ove oznake [latex]\subseteq[/latex] i [latex]\subset[/latex] mozes shvatiti kao "manje ili jednako" i "manje".
Da bismo dokazali da su dva realna broja jednaka, mozemo prvo dokazati da je jedan manji ili jednak drugome i obrnuto, ali ocito, ako vrijedi jednakost onda strogo manje ne moze vrijediti.
hth.
| blob (napisa): | Zanima me kako možemo matematički precizno tvrditi da vrijedi 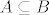 , koliko god da su te dvije mogućnosti ( , koliko god da su te dvije mogućnosti (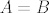 i i 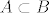 ) intuitivno jasne i očigledne? ) intuitivno jasne i očigledne? |
Da, ovo nisam citirao u gornjem postu a cini mi se da je upravo tu odgovor:
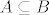 ne znaci isto sto i ne znaci isto sto i
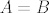 i i 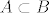 . .
Ove oznake  i i 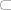 mozes shvatiti kao "manje ili jednako" i "manje". mozes shvatiti kao "manje ili jednako" i "manje".
Da bismo dokazali da su dva realna broja jednaka, mozemo prvo dokazati da je jedan manji ili jednak drugome i obrnuto, ali ocito, ako vrijedi jednakost onda strogo manje ne moze vrijediti.
hth.
_________________
Devious movements in your eyes moved me from relief
Breath comes out white clouds with your lies
and filters through me
|
|
| [Vrh] |
|
blob
Forumaš(ica)


Pridružen/a: 13. 07. 2007. (18:09:52)
Postovi: (23)16
|
 Postano: 21:02 sri, 3. 10. 2007 Naslov: Re: Dokaz da je f(A U B)=f(A) U f(B) Postano: 21:02 sri, 3. 10. 2007 Naslov: Re: Dokaz da je f(A U B)=f(A) U f(B) |
    |
|
|
Ah, sad mi je jasno. :idea:
Krivo sam shvatio što točno znači [latex]f(A \cup B) \subseteq f(A) \cup f(B)[/latex] i precizno značenje oznaka za podskupove pa sam se "malo" izgubio, činilo mi se da je riječ o nečem sasvim trećem.
ß i vsego, puno vam hvala na pomoći ([size=5]i volji da svoje dragocjeno vrijeme trošite na trivijalna brucoška pitanja. hvala, hvala, hvala.[/size])!
:D
edit:
[quote="ß"][quote="blob"] ...koliko god da su te dvije mogućnosti ([latex]A=B[/latex] i [latex]A \subset B[/latex]) [/quote]
[latex]A \subseteq B[/latex] [b]ne znaci[/b] isto sto i
[latex]A=B[/latex] [b]i[/b] [latex]A \subset B[/latex].[/quote]
Ustvari, kad sam gore napisao "dvije mogućnosti", htio sam reći da istovremeno vrijedi samo jedna, dakle ili je A pravi podskup od B ili je A=B. Ali naravno da se ovako kako sam napisao može i drugačije shvatiti.
Ali nije bitno, sad je sve sjelo na svoje mjesto, bar do idućih vježbi iz Analize 8)
Ah, sad mi je jasno. 
Krivo sam shvatio što točno znači 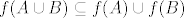 i precizno značenje oznaka za podskupove pa sam se "malo" izgubio, činilo mi se da je riječ o nečem sasvim trećem. i precizno značenje oznaka za podskupove pa sam se "malo" izgubio, činilo mi se da je riječ o nečem sasvim trećem.
ß i vsego, puno vam hvala na pomoći (i volji da svoje dragocjeno vrijeme trošite na trivijalna brucoška pitanja. hvala, hvala, hvala.)!

edit:
| ß (napisa): | | blob (napisa): | ...koliko god da su te dvije mogućnosti (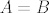 i i 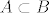 ) ) |
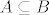 ne znaci isto sto i ne znaci isto sto i
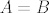 i i 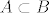 . . |
Ustvari, kad sam gore napisao "dvije mogućnosti", htio sam reći da istovremeno vrijedi samo jedna, dakle ili je A pravi podskup od B ili je A=B. Ali naravno da se ovako kako sam napisao može i drugačije shvatiti.
Ali nije bitno, sad je sve sjelo na svoje mjesto, bar do idućih vježbi iz Analize 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 21:34 sri, 3. 10. 2007 Naslov: Postano: 21:34 sri, 3. 10. 2007 Naslov: |
    |
|
|
Sto se znakovlja tice, ono je malo neprecizno. :(
[latex]\subset[/latex] znaci "podskup", bez jasne specifikacije je l' pravi ili ne; obicno se hvata iz konteksta ili jednostavno nije bitno
[latex]\subseteq[/latex] znaci "podskup", uz mogucnost da su usporedjeni skupovi jednaki
[latex]\subsetneq[/latex] znaci "[b]pravi[/b] podskup"
Ja se trudim koristiti zadnja dva, bas zato da se izbjegne konfuzija. :)
Sto se znakovlja tice, ono je malo neprecizno. 
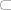 znaci "podskup", bez jasne specifikacije je l' pravi ili ne; obicno se hvata iz konteksta ili jednostavno nije bitno znaci "podskup", bez jasne specifikacije je l' pravi ili ne; obicno se hvata iz konteksta ili jednostavno nije bitno
 znaci "podskup", uz mogucnost da su usporedjeni skupovi jednaki znaci "podskup", uz mogucnost da su usporedjeni skupovi jednaki
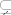 znaci "pravi podskup" znaci "pravi podskup"
Ja se trudim koristiti zadnja dva, bas zato da se izbjegne konfuzija. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
blob
Forumaš(ica)


Pridružen/a: 13. 07. 2007. (18:09:52)
Postovi: (23)16
|
 Postano: 22:25 sri, 3. 10. 2007 Naslov: Postano: 22:25 sri, 3. 10. 2007 Naslov: |
    |
|
|
[quote="vsego"]Sto se znakovlja tice, ono je malo neprecizno. :(
[latex]\subset[/latex] znaci "podskup", bez jasne specifikacije je l' pravi ili ne; obicno se hvata iz konteksta ili jednostavno nije bitno
[latex]\subseteq[/latex] znaci "podskup", uz mogucnost da su usporedjeni skupovi jednaki
[latex]\subsetneq[/latex] znaci "[b]pravi[/b] podskup"
Ja se trudim koristiti zadnja dva, bas zato da se izbjegne konfuzija. :)[/quote]
Jao, baš sad čitam Bronštejna i on pak veli sljedeće:
[quote="I. N. Bronštejn i suradnici"]Neka su A i B skupovi i ako vrijedi [latex]\forall x(x \in A \Rightarrow x \in B)[/latex], onda se A zove [i]podskup[/i] od B. Drugim riječima, A je podskup od B, ako je svaki element iz A ujedno i element od B. [b]Tada pišemo A [/b][latex]\subseteq[/latex] [b]B[/b]. Očito je A [latex]\subseteq[/latex] A. Ako je A [latex]\subseteq[/latex] B i ako u B ima elemenata koji nisu elementi od A, onda se A naziva [i]pravi podskup[/i] od B i [b]piše se A[/b] [latex]\subset[/latex] [b]B[/b].[/quote]
Iako i meni ima više smisla da se pravi podskup označava sa [latex]\subsetneq[/latex] ili, slično, da se kao prava inkluzija označava s [latex]\subsetneqq[/latex] (primjer s vježbi je [latex]\mathbb{N} \subsetneqq \mathbb{Z}\subsetneqq\mathbb{Q}\subsetneqq\mathbb{R}[/latex]), možda je ipak zgodno imati pomutnju simbola (jedni u knjizi, drugi na predavanju, treći na vježbama - primjer za to je redovito korištenje [latex]\wedge[/latex] za konjunkciju na vježbama, a "&" na predavanjima iz EM), jer je to izvrsna vježba za treniranje fleksibilnosti (koja je, u današnjem brzo mijenjajućem svijetu, od itekakve važnosti) :D
| vsego (napisa): | Sto se znakovlja tice, ono je malo neprecizno. 
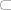 znaci "podskup", bez jasne specifikacije je l' pravi ili ne; obicno se hvata iz konteksta ili jednostavno nije bitno znaci "podskup", bez jasne specifikacije je l' pravi ili ne; obicno se hvata iz konteksta ili jednostavno nije bitno
 znaci "podskup", uz mogucnost da su usporedjeni skupovi jednaki znaci "podskup", uz mogucnost da su usporedjeni skupovi jednaki
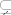 znaci "pravi podskup" znaci "pravi podskup"
Ja se trudim koristiti zadnja dva, bas zato da se izbjegne konfuzija.  |
Jao, baš sad čitam Bronštejna i on pak veli sljedeće:
| I. N. Bronštejn i suradnici (napisa): | Neka su A i B skupovi i ako vrijedi 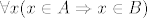 , onda se A zove podskup od B. Drugim riječima, A je podskup od B, ako je svaki element iz A ujedno i element od B. Tada pišemo A , onda se A zove podskup od B. Drugim riječima, A je podskup od B, ako je svaki element iz A ujedno i element od B. Tada pišemo A  B. Očito je A B. Očito je A  A. Ako je A A. Ako je A  B i ako u B ima elemenata koji nisu elementi od A, onda se A naziva pravi podskup od B i piše se A B i ako u B ima elemenata koji nisu elementi od A, onda se A naziva pravi podskup od B i piše se A 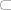 B. B. |
Iako i meni ima više smisla da se pravi podskup označava sa 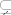 ili, slično, da se kao prava inkluzija označava s ili, slično, da se kao prava inkluzija označava s  (primjer s vježbi je (primjer s vježbi je 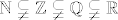 ), možda je ipak zgodno imati pomutnju simbola (jedni u knjizi, drugi na predavanju, treći na vježbama - primjer za to je redovito korištenje ), možda je ipak zgodno imati pomutnju simbola (jedni u knjizi, drugi na predavanju, treći na vježbama - primjer za to je redovito korištenje  za konjunkciju na vježbama, a "&" na predavanjima iz EM), jer je to izvrsna vježba za treniranje fleksibilnosti (koja je, u današnjem brzo mijenjajućem svijetu, od itekakve važnosti) za konjunkciju na vježbama, a "&" na predavanjima iz EM), jer je to izvrsna vježba za treniranje fleksibilnosti (koja je, u današnjem brzo mijenjajućem svijetu, od itekakve važnosti) 
|
|
| [Vrh] |
|
|








