| Prethodna tema :: Sljedeća tema |
| Tko je više cool? |
| Euklid |
|
50% |
[ 6 ] |
| Arhimed |
|
50% |
[ 6 ] |
|
| Ukupno glasova : 12 |
|
| Autor/ica |
Poruka |
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 3:41 ned, 7. 10. 2007 Naslov: Bestijarij kruznica Postano: 3:41 ned, 7. 10. 2007 Naslov: Bestijarij kruznica |
    |
|
|
Slično kao i kod [url=http://degiorgi.math.hr/forum/viewtopic.php?t=10092]bestijarija cetverokuta[/url], definirajte neke vama zanimljive kružnice. Kružnicu ne treba definirati.
Ja ću početi s Arhimedovim kružnicama.
Konstruirajmo tri kružnice sa kolinearnim središtima tako da se dvije diraju izvana u nekoj točki C, a neka treća dira te dvije u točkama A i B.
[img]http://degiorgi.math.hr/forum/files/sl1_118.png[/img]
Kružnicu, koja dira okomicu na pravac AB u točki C i po dvije od prethodno spomenutih kružnica (jednu izvana i jednu iznutra), zovemo [b]Arhimedova kružnica[/b].
Ukratko neka svojstva:
Slika sugerira da "iznad" pravca AB ("ispod" pravca AB je sve simetrično) postoje dvije Arhimedove kružnice i lako se dokaže da [u]obje imaju jednak radijus[/u].
Ako označimo s [latex]2r_1=AC[/latex] i [latex]2r_2=CB[/latex], onda je radijus Arhimedovih kružnica jednak [latex]\frac{r_1 r_2}{r_1 + r_2}[/latex].
Te dvije kružnice se često nazivaju Arhimedovim blizancima (the twin circles of Archimedes).
Slično kao i kod bestijarija cetverokuta, definirajte neke vama zanimljive kružnice. Kružnicu ne treba definirati.
Ja ću početi s Arhimedovim kružnicama.
Konstruirajmo tri kružnice sa kolinearnim središtima tako da se dvije diraju izvana u nekoj točki C, a neka treća dira te dvije u točkama A i B.
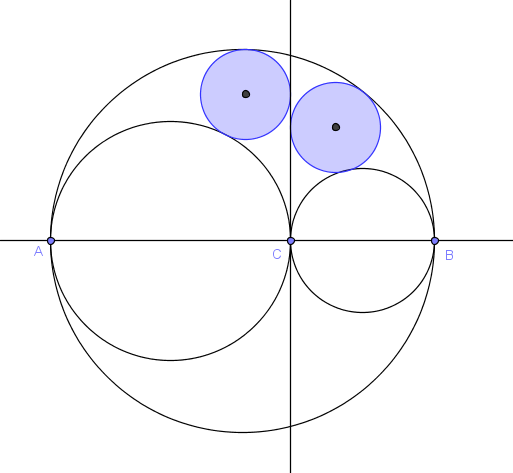
Kružnicu, koja dira okomicu na pravac AB u točki C i po dvije od prethodno spomenutih kružnica (jednu izvana i jednu iznutra), zovemo Arhimedova kružnica.
Ukratko neka svojstva:
Slika sugerira da "iznad" pravca AB ("ispod" pravca AB je sve simetrično) postoje dvije Arhimedove kružnice i lako se dokaže da obje imaju jednak radijus.
Ako označimo s 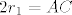 i i 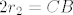 , onda je radijus Arhimedovih kružnica jednak , onda je radijus Arhimedovih kružnica jednak 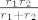 . .
Te dvije kružnice se često nazivaju Arhimedovim blizancima (the twin circles of Archimedes).
_________________
The Dude Abides
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 19:19 ned, 7. 10. 2007 Naslov: Postano: 19:19 ned, 7. 10. 2007 Naslov: |
    |
|
|
[b]Pappusova[/b] kružnica.
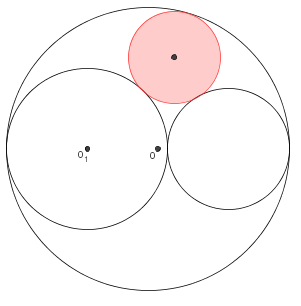
Ako, na isti način kao i kod Arhimedovih kružnica, konstruiramo tri međusobno tangentne kružnice, onda kružnicu koja dira sve tri kružnice (dvije izvana i jednu iznutra) zovemo Pappusova kružnica.
[img]http://degiorgi.math.hr/forum/files/sl2_113.png[/img]
Može se pokazati da središte Pappusove kružnice leži na elipsi sa žarištima u točkama O i O1, gdje je točka O središte "velike" kružnice, a O1 središte jedne od manjih kružnica.
Pappusova kružnica je jedno rješenje specijalnog slučaja [url=http://www.cut-the-knot.org/Curriculum/Geometry/Apollonius.shtml]Apolonijevog problema[/url].
Pappusova kružnica.
Ako, na isti način kao i kod Arhimedovih kružnica, konstruiramo tri međusobno tangentne kružnice, onda kružnicu koja dira sve tri kružnice (dvije izvana i jednu iznutra) zovemo Pappusova kružnica.
Može se pokazati da središte Pappusove kružnice leži na elipsi sa žarištima u točkama O i O1, gdje je točka O središte "velike" kružnice, a O1 središte jedne od manjih kružnica.
Pappusova kružnica je jedno rješenje specijalnog slučaja Apolonijevog problema.
_________________
The Dude Abides
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 2:26 pon, 8. 10. 2007 Naslov: Postano: 2:26 pon, 8. 10. 2007 Naslov: |
    |
|
|
[b]Feuerbachova[/b] kružnica ili [b]kružnica devet točaka[/b].
Neka su točke G, H, I nožišta visina iz vrhova A, B, C, točke D, E, F polovišta stranica BC, AC, AB, a točke J, K, L polovišta dužina AS, BS, CS gdje je točka S ortocentar.
[img]http://upload.wikimedia.org/wikipedia/commons/thumb/7/71/Nine-point_circle.svg/364px-Nine-point_circle.svg.png[/img]
Tih devet točaka trokuta ABC leže na kružnici koju zovemo Feuerbachova kružnica.
Feuerbachova kružnica ili kružnica devet točaka.
Neka su točke G, H, I nožišta visina iz vrhova A, B, C, točke D, E, F polovišta stranica BC, AC, AB, a točke J, K, L polovišta dužina AS, BS, CS gdje je točka S ortocentar.

Tih devet točaka trokuta ABC leže na kružnici koju zovemo Feuerbachova kružnica.
_________________
The Dude Abides
|
|
| [Vrh] |
|
|









