| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 9:55 sri, 14. 11. 2007 Naslov: Otvorenost i zatvorenost IN, Z, IQ u IR Postano: 9:55 sri, 14. 11. 2007 Naslov: Otvorenost i zatvorenost IN, Z, IQ u IR |
    |
|
|
Razmisljate li isto :wink: :
[b]IN nije otvoren ali je zatvoren.[/b]
IN nije otvoren jer (otvorena)kugla odnosno interval(u IR kugla je interval) oko proizvoljnog prirodnog broja nije sadrzana u IN.
(proizvoljno malen interval oko prirodnog broja osim njega samog "zahvaca" barem jedan broj koji nije iz IN(racionalan, iracionalan))
IN je zatvoren jer je njegov komplement otvoren.
(Komplement od IN je IR\IN, a on je otvoren jer postoji interval oko proizvoljnog elementa iz IR\IN sadrzan u IR\IN)
[b]Z nije otvoren ali je zatvoren[\b].
Analogno razmisljanje.
[b]IQ nije otvoren, a nije ni zatvoren[\b].
QI nije otvoren jer svaki interval oko proizvoljnog broja sadrzi barem jedan iracionalan broj(bliskost iracionalnih i racionalnih brojeva) pa taj interval nije "uronjen" u IQ.
IQ nije ni zatvoren jer ukoliko bi bio zatvoren tada bi njegov komplement morao biti otvoren, a njegov komplement( IR\IQ) nije otvoren zbog spomenute bliskosti(bliskost je simetricna relacija -> ako si ti blizak samnom onda sam i ja s tobom :mrgreen: ) odnosno proizvoljan interval proizvoljnog iracionalnog broja sadrzi barem jednu racionalnu tocku pa taj interval nije sadrzan u IR\IQ.
Razmisljate li isto  : :
IN nije otvoren ali je zatvoren.
IN nije otvoren jer (otvorena)kugla odnosno interval(u IR kugla je interval) oko proizvoljnog prirodnog broja nije sadrzana u IN.
(proizvoljno malen interval oko prirodnog broja osim njega samog "zahvaca" barem jedan broj koji nije iz IN(racionalan, iracionalan))
IN je zatvoren jer je njegov komplement otvoren.
(Komplement od IN je IR\IN, a on je otvoren jer postoji interval oko proizvoljnog elementa iz IR\IN sadrzan u IR\IN)
[b]Z nije otvoren ali je zatvoren[\b].
Analogno razmisljanje.
[b]IQ nije otvoren, a nije ni zatvoren[\b].
QI nije otvoren jer svaki interval oko proizvoljnog broja sadrzi barem jedan iracionalan broj(bliskost iracionalnih i racionalnih brojeva) pa taj interval nije "uronjen" u IQ.
IQ nije ni zatvoren jer ukoliko bi bio zatvoren tada bi njegov komplement morao biti otvoren, a njegov komplement( IR\IQ) nije otvoren zbog spomenute bliskosti(bliskost je simetricna relacija → ako si ti blizak samnom onda sam i ja s tobom  ) odnosno proizvoljan interval proizvoljnog iracionalnog broja sadrzi barem jednu racionalnu tocku pa taj interval nije sadrzan u IR\IQ. ) odnosno proizvoljan interval proizvoljnog iracionalnog broja sadrzi barem jednu racionalnu tocku pa taj interval nije sadrzan u IR\IQ.
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
 Postano: 11:54 sri, 14. 11. 2007 Naslov: Postano: 11:54 sri, 14. 11. 2007 Naslov: |
    |
|
|
[quote="Luuka"]I ja razmišljam isto...samo ne znam kaj će ti taj I kod svega... :lol: [/quote]
Slovo I nalaze masnocu(boldanost) oznake skupa prirodnih, racionalnih i realnih. Jasno je da IZ ili ZI ne nalaze nista pa nije ni upotrebljen za skup cijelih. :mrgreen:
Vidim dvije vazne cinjenice bitne su za dokazivanje zadataka ovog tipa:
1. Svaki se realan broj proizvoljno dobro aproksimira racionalnim brojem.
2. Postoji prirodan broj takav da koliko god proizvoljno malen pozitivan broj epsilon uzmemo vrijedi 1/n < Epsilon (Eudokso-Arhimedov aksiom(zapravo teorem)).
Zahvaljujuci E-Au potrebno je "samo" nastimavati epsilon.
[b]
Eudokso-Arhimedov aksiom:
a, b > 0
Postoji n takav da je na > b
[/b]
Podijelim nejednakost sa a i uzmem reciprocno:
1/n < b/a
za a = 1 imam 1/n < b za b>0 (b = Epsilon) i time vrijedi da za svaki Epsilon postoji n takav da 1/n < Epsilon.
Evo i razmisljanje zasto je zatvarac od IQ IR:
Q nije otvoren niti zatvoren.
Zatvarac je po definiciji najmanji zatvoren u kojem je Q uronjen.
Intuitivno :mrgreen: zakljucujem da je zatvarac od Q IR.
Idem pretpostavit da je postoji manji zatvoren skup koji sadrzi Q, recimo kada bi iz IR izbacio samo jednu iracionalnu tocku i taj skup(IR\{x}, x irac) proglasio zatvaracem, taj bi skup morao biti zatvoren dakle njegov komplement bi morao biti otvoren. Ali njegov komplement je jednoclan skup {x} koji je zatvoren.
| Luuka (napisa): | I ja razmišljam isto...samo ne znam kaj će ti taj I kod svega...  |
Slovo I nalaze masnocu(boldanost) oznake skupa prirodnih, racionalnih i realnih. Jasno je da IZ ili ZI ne nalaze nista pa nije ni upotrebljen za skup cijelih. 
Vidim dvije vazne cinjenice bitne su za dokazivanje zadataka ovog tipa:
1. Svaki se realan broj proizvoljno dobro aproksimira racionalnim brojem.
2. Postoji prirodan broj takav da koliko god proizvoljno malen pozitivan broj epsilon uzmemo vrijedi 1/n < Epsilon (Eudokso-Arhimedov aksiom(zapravo teorem)).
Zahvaljujuci E-Au potrebno je "samo" nastimavati epsilon.
Eudokso-Arhimedov aksiom:
a, b > 0
Postoji n takav da je na > b
Podijelim nejednakost sa a i uzmem reciprocno:
1/n < b/a
za a = 1 imam 1/n < b za b>0 (b = Epsilon) i time vrijedi da za svaki Epsilon postoji n takav da 1/n < Epsilon.
Evo i razmisljanje zasto je zatvarac od IQ IR:
Q nije otvoren niti zatvoren.
Zatvarac je po definiciji najmanji zatvoren u kojem je Q uronjen.
Intuitivno  zakljucujem da je zatvarac od Q IR. zakljucujem da je zatvarac od Q IR.
Idem pretpostavit da je postoji manji zatvoren skup koji sadrzi Q, recimo kada bi iz IR izbacio samo jednu iracionalnu tocku i taj skup(IR\{x}, x irac) proglasio zatvaracem, taj bi skup morao biti zatvoren dakle njegov komplement bi morao biti otvoren. Ali njegov komplement je jednoclan skup {x} koji je zatvoren.
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 12:35 sri, 14. 11. 2007 Naslov: Postano: 12:35 sri, 14. 11. 2007 Naslov: |
    |
|
|
[quote="RonnieColeman"]Evo i razmisljanje zasto je zatvarac od IQ IR:
Q nije otvoren niti zatvoren.
Zatvarac je po definiciji najmanji zatvoren u kojem je Q uronjen.
Intuitivno :mrgreen: zakljucujem da je zatvarac od Q IR.
Idem pretpostavit da je postoji manji zatvoren skup koji sadrzi Q, recimo kada bi iz IR izbacio samo jednu iracionalnu tocku i taj skup(IR\{x}, x irac) proglasio zatvaracem, taj bi skup morao biti zatvoren dakle njegov komplement bi morao biti otvoren. Ali njegov komplement je jednoclan skup {x} koji je zatvoren.[/quote]
IMO, losa argumentacija, jer ju induktivno mozes prosiriti na "izbacim [b]konacno mnogo[/b] iracionalnih tocaka", ali ne i na "izbacim neke iracionalne tocke (ukljucivo i njih beskonacno mnogo)". :?
Recimo, izbacim skup svih iracionalnih tocaka koje na 17. mjestu iza decimalne tocke imaju znamenku 7. :shock:
Prepustim tebi da dokazes korektno. ;)
| RonnieColeman (napisa): | Evo i razmisljanje zasto je zatvarac od IQ IR:
Q nije otvoren niti zatvoren.
Zatvarac je po definiciji najmanji zatvoren u kojem je Q uronjen.
Intuitivno  zakljucujem da je zatvarac od Q IR. zakljucujem da je zatvarac od Q IR.
Idem pretpostavit da je postoji manji zatvoren skup koji sadrzi Q, recimo kada bi iz IR izbacio samo jednu iracionalnu tocku i taj skup(IR\{x}, x irac) proglasio zatvaracem, taj bi skup morao biti zatvoren dakle njegov komplement bi morao biti otvoren. Ali njegov komplement je jednoclan skup {x} koji je zatvoren. |
IMO, losa argumentacija, jer ju induktivno mozes prosiriti na "izbacim konacno mnogo iracionalnih tocaka", ali ne i na "izbacim neke iracionalne tocke (ukljucivo i njih beskonacno mnogo)". 
Recimo, izbacim skup svih iracionalnih tocaka koje na 17. mjestu iza decimalne tocke imaju znamenku 7. 
Prepustim tebi da dokazes korektno. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
Blatko
Forumaš(ica)

Pridružen/a: 12. 07. 2007. (11:25:44)
Postovi: (5D)16
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 14:24 sri, 14. 11. 2007 Naslov: Postano: 14:24 sri, 14. 11. 2007 Naslov: |
    |
|
|
[quote="RonnieColeman"]
Evo i razmisljanje zasto je zatvarac od IQ IR:
Q nije otvoren niti zatvoren.
Zatvarac je po definiciji najmanji zatvoren u kojem je Q uronjen.
Intuitivno :mrgreen: zakljucujem da je zatvarac od Q IR.
Idem pretpostavit da je postoji manji zatvoren skup koji sadrzi Q, recimo kada bi iz IR izbacio samo jednu iracionalnu tocku i taj skup(IR\{x}, x irac) proglasio zatvaracem, taj bi skup morao biti zatvoren dakle njegov komplement bi morao biti otvoren. Ali njegov komplement je jednoclan skup {x} koji je zatvoren.[/quote]
meni je ljepse ovako:
[latex] x \in \mathbb{R}[/latex] proizvoljan, i svaka [latex] K(x, \epsilon ) [/latex] sadrzi barem jednu racionalnu tocku (jer je [latex] \mathbb{Q} [/latex] gust u [latex] \mathbb{R} [/latex] ), pa je [latex] x \in \mathbb{R}[/latex] gomiliste. kako je [latex] \overline{ \mathbb{Q} } = \mathbb{Q} \cup \{ gomilista \ od \ \mathbb{Q} \} \Rightarrow \mathbb{R} \subseteq \overline{ \mathbb{Q} } [/latex].
obratna inkluzija vrijedi jer smo u jednoj dimenziji.
| RonnieColeman (napisa): |
Evo i razmisljanje zasto je zatvarac od IQ IR:
Q nije otvoren niti zatvoren.
Zatvarac je po definiciji najmanji zatvoren u kojem je Q uronjen.
Intuitivno  zakljucujem da je zatvarac od Q IR. zakljucujem da je zatvarac od Q IR.
Idem pretpostavit da je postoji manji zatvoren skup koji sadrzi Q, recimo kada bi iz IR izbacio samo jednu iracionalnu tocku i taj skup(IR\{x}, x irac) proglasio zatvaracem, taj bi skup morao biti zatvoren dakle njegov komplement bi morao biti otvoren. Ali njegov komplement je jednoclan skup {x} koji je zatvoren. |
meni je ljepse ovako:
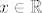 proizvoljan, i svaka proizvoljan, i svaka 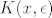 sadrzi barem jednu racionalnu tocku (jer je sadrzi barem jednu racionalnu tocku (jer je 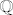 gust u gust u 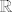 ), pa je ), pa je 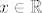 gomiliste. kako je gomiliste. kako je 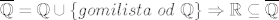 . .
obratna inkluzija vrijedi jer smo u jednoj dimenziji.
_________________
Rafael Mrđen
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
 Postano: 22:41 sri, 14. 11. 2007 Naslov: Postano: 22:41 sri, 14. 11. 2007 Naslov: |
    |
|
|
[quote="vsego"][quote="RonnieColeman"]Evo i razmisljanje zasto je zatvarac od IQ IR:
Q nije otvoren niti zatvoren.
Zatvarac je po definiciji najmanji zatvoren u kojem je Q uronjen.
Intuitivno :mrgreen: zakljucujem da je zatvarac od Q IR.
Idem pretpostavit da je postoji manji zatvoren skup koji sadrzi Q, recimo kada bi iz IR izbacio samo jednu iracionalnu tocku i taj skup(IR\{x}, x irac) proglasio zatvaracem, taj bi skup morao biti zatvoren dakle njegov komplement bi morao biti otvoren. Ali njegov komplement je jednoclan skup {x} koji je zatvoren.[/quote]
IMO, losa argumentacija, jer ju induktivno mozes prosiriti na "izbacim [b]konacno mnogo[/b] iracionalnih tocaka", ali ne i na "izbacim neke iracionalne tocke (ukljucivo i njih beskonacno mnogo)". :?
Recimo, izbacim skup svih iracionalnih tocaka koje na 17. mjestu iza decimalne tocke imaju znamenku 7. :shock:
[/quote]
Ok, izbacim beskonacno mnogo iracionalnih sa gornjim svojstvom(17. mjesto iza decimalne tocke ima znamenku 7).
Okupim(stavim u skup) te iracionalne brojeve pod oznakom X.
Imam IR\X.
Kada bi IR\X bio zatvarac od IQ, dakle zatvoren, tada bi njegov komplement morao biti otvoren.
Komplement od IR\X je X, a on nije otvoren jer svaka kuglica(interval) oko proizvoljne iracionalne tocke iz X se ne moze uroniti u X(jer je "zagadjena" barem jednom racionalnom tockom).
Dakle, izbacivanjem beskonacno brojeva iz IR\IQ nece dati zatvoren skup koji sadrzi IQ.
Sve iracionalne(njih prebrojivo mnogo) ne smijem izbaciti jer mi ostaje samo IQ koji nije zatvoren.
Dakle, svi iracionalni su mi potrebiti jer izbacim li jedan, konacno, beskonacno ili prebrojivo beskonacno njih, ne dobivam zatvoren skup koji sadrzi IQ pa je najmanji zatvoren skup sto sadrzi IQ upravo univerzalni skup za nase razmatranje, dakle IR.
[quote][b]Rafael wrote[/b]
... smo u jednoj dimenziji. [/quote]
Sto ti to znaci?
Znaci li ti to da zatvarac od IQ nema izbora nego biti podskup od IR s obzirom da je IR univerzalan skup?
| vsego (napisa): | | RonnieColeman (napisa): | Evo i razmisljanje zasto je zatvarac od IQ IR:
Q nije otvoren niti zatvoren.
Zatvarac je po definiciji najmanji zatvoren u kojem je Q uronjen.
Intuitivno  zakljucujem da je zatvarac od Q IR. zakljucujem da je zatvarac od Q IR.
Idem pretpostavit da je postoji manji zatvoren skup koji sadrzi Q, recimo kada bi iz IR izbacio samo jednu iracionalnu tocku i taj skup(IR\{x}, x irac) proglasio zatvaracem, taj bi skup morao biti zatvoren dakle njegov komplement bi morao biti otvoren. Ali njegov komplement je jednoclan skup {x} koji je zatvoren. |
IMO, losa argumentacija, jer ju induktivno mozes prosiriti na "izbacim konacno mnogo iracionalnih tocaka", ali ne i na "izbacim neke iracionalne tocke (ukljucivo i njih beskonacno mnogo)". 
Recimo, izbacim skup svih iracionalnih tocaka koje na 17. mjestu iza decimalne tocke imaju znamenku 7. 
|
Ok, izbacim beskonacno mnogo iracionalnih sa gornjim svojstvom(17. mjesto iza decimalne tocke ima znamenku 7).
Okupim(stavim u skup) te iracionalne brojeve pod oznakom X.
Imam IR\X.
Kada bi IR\X bio zatvarac od IQ, dakle zatvoren, tada bi njegov komplement morao biti otvoren.
Komplement od IR\X je X, a on nije otvoren jer svaka kuglica(interval) oko proizvoljne iracionalne tocke iz X se ne moze uroniti u X(jer je "zagadjena" barem jednom racionalnom tockom).
Dakle, izbacivanjem beskonacno brojeva iz IR\IQ nece dati zatvoren skup koji sadrzi IQ.
Sve iracionalne(njih prebrojivo mnogo) ne smijem izbaciti jer mi ostaje samo IQ koji nije zatvoren.
Dakle, svi iracionalni su mi potrebiti jer izbacim li jedan, konacno, beskonacno ili prebrojivo beskonacno njih, ne dobivam zatvoren skup koji sadrzi IQ pa je najmanji zatvoren skup sto sadrzi IQ upravo univerzalni skup za nase razmatranje, dakle IR.
| Citat: | Rafael wrote
... smo u jednoj dimenziji. |
Sto ti to znaci?
Znaci li ti to da zatvarac od IQ nema izbora nego biti podskup od IR s obzirom da je IR univerzalan skup?
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 3:10 čet, 15. 11. 2007 Naslov: Postano: 3:10 čet, 15. 11. 2007 Naslov: |
    |
|
|
[quote="RonnieColeman"]Dakle, izbacivanjem beskonacno brojeva iz IR\IQ nece dati zatvoren skup koji sadrzi IQ.[/quote]
Krivo; tocno je:
"Dakle, izbacivanjem beskonacno brojeva iz IR\IQ [color=red]prema gore navedenom pravilu[/color] nece dati zatvoren skup koji sadrzi IQ."
Imas ovdje dovoljno dobrih dokaza konkretnog problema zatvaraca od [latex]\textstyle\mathbb{Q}[/latex] u [latex]\textstyle\mathbb{R}[/latex]; ja ti samo pokusavam ukazati na to da ne mozes zakljucivati na nacin na koji to radis. :ccc: Kao da zakljucis da parnih brojeva u [latex]\textstyle\mathbb{N}[/latex] ima vise od prebrojivo mnogo jer ih ne mozes pokupiti skupom [latex]\textstyle S:=\{2^n:\ n\in\mathbb{N}\}[/latex]. :) Dokaz mora biti opcenit, a ne "pokopao sam pravilo koje je vsego izcuclao iz malog prsta, pa zato generalno mogu zakljuciti da nesto vrijedi za svaki beskonacni podskup skupa iracionalnih brojeva". :)
Nadam se da je sada jasnije; ako nije - pitaj. ;) Bitno je shvatiti kako se nesto (ne) moze dokazati. :prodike:
| RonnieColeman (napisa): | | Dakle, izbacivanjem beskonacno brojeva iz IR\IQ nece dati zatvoren skup koji sadrzi IQ. |
Krivo; tocno je:
"Dakle, izbacivanjem beskonacno brojeva iz IR\IQ prema gore navedenom pravilu nece dati zatvoren skup koji sadrzi IQ."
Imas ovdje dovoljno dobrih dokaza konkretnog problema zatvaraca od 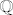 u u 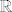 ; ja ti samo pokusavam ukazati na to da ne mozes zakljucivati na nacin na koji to radis. ; ja ti samo pokusavam ukazati na to da ne mozes zakljucivati na nacin na koji to radis.  Kao da zakljucis da parnih brojeva u Kao da zakljucis da parnih brojeva u 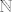 ima vise od prebrojivo mnogo jer ih ne mozes pokupiti skupom ima vise od prebrojivo mnogo jer ih ne mozes pokupiti skupom 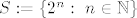 . .  Dokaz mora biti opcenit, a ne "pokopao sam pravilo koje je vsego izcuclao iz malog prsta, pa zato generalno mogu zakljuciti da nesto vrijedi za svaki beskonacni podskup skupa iracionalnih brojeva". Dokaz mora biti opcenit, a ne "pokopao sam pravilo koje je vsego izcuclao iz malog prsta, pa zato generalno mogu zakljuciti da nesto vrijedi za svaki beskonacni podskup skupa iracionalnih brojeva". 
Nadam se da je sada jasnije; ako nije - pitaj.  Bitno je shvatiti kako se nesto (ne) moze dokazati. Bitno je shvatiti kako se nesto (ne) moze dokazati. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
|
| [Vrh] |
|
|














