| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
5ra
Forumaš(ica)


Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 12:03 čet, 8. 11. 2007 Naslov: Postano: 12:03 čet, 8. 11. 2007 Naslov: |
    |
|
|
Eto ja krenuo rješavat...Dokazah 1.,2.,3.,10.
11. zatv,zatv,ništa,zatv,otv
12. x iz [0,1]
x iz [0,1] U {2}
x iz [0,1], y=1
d i e ne znam...zasad... :lol:
Eto ja krenuo rješavat...Dokazah 1.,2.,3.,10.
11. zatv,zatv,ništa,zatv,otv
12. x iz [0,1]
x iz [0,1] U {2}
x iz [0,1], y=1
d i e ne znam...zasad... 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
noa
Forumaš(ica)
Pridružen/a: 14. 04. 2007. (22:28:08)
Postovi: (51)16
|
|
| [Vrh] |
|
noa
Forumaš(ica)
Pridružen/a: 14. 04. 2007. (22:28:08)
Postovi: (51)16
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 19:18 ned, 11. 11. 2007 Naslov: Postano: 19:18 ned, 11. 11. 2007 Naslov: |
    |
|
|
[quote="noa"]kako si dokazao 2 ?? i bi li netko mogao objasniti kako se rjesavaju zadatci kao 5, tj. svi u kojima je zadano da je norma manja veca ili jednaka necemu ne znam kako to dokazati[/quote]
mislim da se peti moze ovako: skup [latex]S[/latex] je ocito jedinicna sfera u [latex]R^{n}[/latex], tj. [latex]S= \partial K(0,1) = Cl( K(0,1) ) \cap Cl ( \mathbb{R} ^{n}} \setminus K(0,1))}[/latex] a to je presjek dva zatvorena skupa, pa je zatvoren, i nije otvoren (jer nije prazan skup)
P.S. Cl mi znaci zatvarac skupa. kako se u latexu povuce crta iznad K(0,1) ?
| noa (napisa): | | kako si dokazao 2 ?? i bi li netko mogao objasniti kako se rjesavaju zadatci kao 5, tj. svi u kojima je zadano da je norma manja veca ili jednaka necemu ne znam kako to dokazati |
mislim da se peti moze ovako: skup  je ocito jedinicna sfera u je ocito jedinicna sfera u 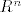 , tj. , tj. 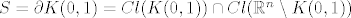 a to je presjek dva zatvorena skupa, pa je zatvoren, i nije otvoren (jer nije prazan skup) a to je presjek dva zatvorena skupa, pa je zatvoren, i nije otvoren (jer nije prazan skup)
P.S. Cl mi znaci zatvarac skupa. kako se u latexu povuce crta iznad K(0,1) ?
_________________
Rafael Mrđen
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Blatko
Forumaš(ica)

Pridružen/a: 12. 07. 2007. (11:25:44)
Postovi: (5D)16
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
 Postano: 0:03 pon, 12. 11. 2007 Naslov: Postano: 0:03 pon, 12. 11. 2007 Naslov: |
    |
|
|
[quote="rafaelm"][quote="noa"]kako si dokazao 2 ?? i bi li netko mogao objasniti kako se rjesavaju zadatci kao 5, tj. svi u kojima je zadano da je norma manja veca ili jednaka necemu ne znam kako to dokazati[/quote]
mislim da se peti moze ovako: skup [latex]S[/latex] je ocito jedinicna sfera u [latex]R^{n}[/latex], tj. [latex]S= \partial K(0,1) = Cl( K(0,1) ) \cap Cl ( \mathbb{R} ^{n}} \setminus K(0,1))}[/latex] a to je presjek dva zatvorena skupa, pa je zatvoren, i nije otvoren (jer nije prazan skup)
P.S. Cl mi znaci zatvarac skupa. kako se u latexu povuce crta iznad K(0,1) ?[/quote]
Dali onda od tuda možemo zaključiti u 6. da je [latex] Cl(S)=\partial K(0,1)\Rightarrow Int(S)=\emptyset \Rightarrow \partial S=Cl(S) [/latex]
Dali tu treba još nešto dodatno dokazivat?
| rafaelm (napisa): | | noa (napisa): | | kako si dokazao 2 ?? i bi li netko mogao objasniti kako se rjesavaju zadatci kao 5, tj. svi u kojima je zadano da je norma manja veca ili jednaka necemu ne znam kako to dokazati |
mislim da se peti moze ovako: skup  je ocito jedinicna sfera u je ocito jedinicna sfera u 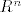 , tj. , tj. 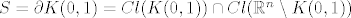 a to je presjek dva zatvorena skupa, pa je zatvoren, i nije otvoren (jer nije prazan skup) a to je presjek dva zatvorena skupa, pa je zatvoren, i nije otvoren (jer nije prazan skup)
P.S. Cl mi znaci zatvarac skupa. kako se u latexu povuce crta iznad K(0,1) ? |
Dali onda od tuda možemo zaključiti u 6. da je 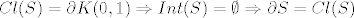
Dali tu treba još nešto dodatno dokazivat?
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
 Postano: 12:52 ned, 18. 11. 2007 Naslov: Re: Neprekidna funkcija Postano: 12:52 ned, 18. 11. 2007 Naslov: Re: Neprekidna funkcija |
    |
|
|
[quote="matmih"]Kada bi imali neprekidnu funkciju [latex] f:\mathbb{R}^2 \rightarrow \mathbb{R}, f(x,y)=x^2+y^2-5<0[/latex] tada je [latex] f(x,y)\in [-5,0> [/latex]
Šta možemo zaključiti o [latex] f^{-1}([-5,0>)[/latex]?[/quote]
Kako si iz ovoga dobio da je -5 ukljuceno? :?
I sta ne bi onda islo da je f(x,y) element <-besk, 0> sto je otvoreno, pa je zbog neprekidnosti od f i f-1(<-besk, 0>) takodjer otvoreno?
| matmih (napisa): | Kada bi imali neprekidnu funkciju 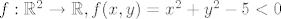 tada je tada je 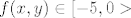
Šta možemo zaključiti o 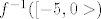 ? ? |
Kako si iz ovoga dobio da je -5 ukljuceno? 
I sta ne bi onda islo da je f(x,y) element ←besk, 0> sto je otvoreno, pa je zbog neprekidnosti od f i f-1(←besk, 0>) takodjer otvoreno?
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
 Postano: 13:05 ned, 18. 11. 2007 Naslov: Postano: 13:05 ned, 18. 11. 2007 Naslov: |
    |
|
|
Nije mi ovo baš sasvim jasno zato i pitam.
Ali najmanja vrijednosti koju f(x,y) može poprimiti je 0 za x=y=0,a to je -5, za ostale kombinacije x i y ćemo dobiti nešto >0, a pošto je zadano da f(x,y)<0, zato mislim da je slika između -5 i 0, dali gledam nešto krivo?
Nije mi ovo baš sasvim jasno zato i pitam.
Ali najmanja vrijednosti koju f(x,y) može poprimiti je 0 za x=y=0,a to je -5, za ostale kombinacije x i y ćemo dobiti nešto >0, a pošto je zadano da f(x,y)<0, zato mislim da je slika između -5 i 0, dali gledam nešto krivo?
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
 Postano: 13:10 ned, 18. 11. 2007 Naslov: Postano: 13:10 ned, 18. 11. 2007 Naslov: |
    |
|
|
[quote="matmih"]Nije mi ovo baš sasvim jasno zato i pitam.
Ali najmanja vrijednosti koju f(x,y) može poprimiti je 0 za x=y=0,a to je -5, za ostale kombinacije x i y ćemo dobiti nešto >0, a pošto je zadano da f(x,y)<0, zato mislim da je slika između -5 i 0, dali gledam nešto krivo?[/quote]
Istina da, to nisam niti gledala...
Ako cemo tako, onda bi to valjda bilo da nije ni otvoreno ni zatvoreno...Ali sad vise niti ja nisam sigurna.
| matmih (napisa): | Nije mi ovo baš sasvim jasno zato i pitam.
Ali najmanja vrijednosti koju f(x,y) može poprimiti je 0 za x=y=0,a to je -5, za ostale kombinacije x i y ćemo dobiti nešto >0, a pošto je zadano da f(x,y)<0, zato mislim da je slika između -5 i 0, dali gledam nešto krivo? |
Istina da, to nisam niti gledala...
Ako cemo tako, onda bi to valjda bilo da nije ni otvoreno ni zatvoreno...Ali sad vise niti ja nisam sigurna.
|
|
| [Vrh] |
|
kika
Forumaš(ica)

Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
 Postano: 13:26 ned, 18. 11. 2007 Naslov: Re: Neprekidna funkcija Postano: 13:26 ned, 18. 11. 2007 Naslov: Re: Neprekidna funkcija |
    |
|
|
[quote="matmih"]Kada bi imali neprekidnu funkciju [latex] f:\mathbb{R}^2 \rightarrow \mathbb{R}, f(x,y)=x^2+y^2-5<0[/latex] tada je [latex] f(x,y)\in [-5,0> [/latex]
Šta možemo zaključiti o [latex] f^{-1}([-5,0>)[/latex]?[/quote]
kako glasi tocno zadatak?vjerojatno da li je A={(x,y)e Rn: x^2+yˇ2-5<0} otvoren ili zatvoren.
Ako glasi tako,onda uzmemo f(x,y)=x^2+y^2.i ta f(x,y) je neprekidna.
(i onda je f(x,y)<5).
A f-1(<-besk.,5>).
<-bes.,5>je otvoren interval,pa je i f-1(<-bes.,5>) otvoren.
A f-1(<-bes.,5>)je jednak promatranom skupu A pa je i on otvoren.
| matmih (napisa): | Kada bi imali neprekidnu funkciju 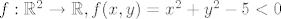 tada je tada je 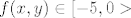
Šta možemo zaključiti o 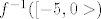 ? ? |
kako glasi tocno zadatak?vjerojatno da li je A={(x,y)e Rn: x^2+yˇ2-5<0} otvoren ili zatvoren.
Ako glasi tako,onda uzmemo f(x,y)=x^2+y^2.i ta f(x,y) je neprekidna.
(i onda je f(x,y)<5).
A f-1(←besk.,5>).
←bes.,5>je otvoren interval,pa je i f-1(←bes.,5>) otvoren.
A f-1(←bes.,5>)je jednak promatranom skupu A pa je i on otvoren.
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
Blatko
Forumaš(ica)

Pridružen/a: 12. 07. 2007. (11:25:44)
Postovi: (5D)16
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
|



















