| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
sestrabracegrim
Forumaš(ica)

Pridružen/a: 14. 04. 2007. (16:45:31)
Postovi: (6)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:07 pon, 26. 11. 2007 Naslov: Postano: 18:07 pon, 26. 11. 2007 Naslov: |
    |
|
|
Rađeno je na vježbama ;)
Primjer iz glave (rađen baš na predavanju):
[latex]\sum_{k=0}^{n}{{n \choose k}^{2}}={2n \choose n}[/latex]
Desna strana: odabir n ljudi iz grupe od 2n ljudi.
Lijeva strana: prvo zanemariš sumu i gledaš kaj imaš. Pa se sjetiš simetrije binomnog koeficijenta pa imaš [latex]{n \choose k}{n \choose n-k}[/latex]
A to je odabir k ljudi (recimo dječaka) od njih n, i odabir n-k ljudi (recimo djevojčica) od njih n...kad sumiraš po svim k, dobije se baš broj odabira n ljudi iz grupe od 2n.
Trivijalan primjer:
[latex]{n \choose k}={n \choose n-k}[/latex]
lijeva strana: odabir k ljudi od njih n.
desna strana: odabir n-k ljudi od njih n, a to je komplement od ovog prvog, pa je broj načina isti.
A dosta ih ide na foru nekakvog istaknutog člana...kad imaš na jednoj strani nešto, a na drugoj neka 2 člana pa između +.
Pa kažeš da je ovo lijevo (recimo) odabir k ljudi od n, a desno istaknemo neki član pa ako on je među odabranima, onda trebamo još k-1 od n-1, a ako nije onda trebamo još k od n-1. To je dokaz ovog:
[latex]{n \choose k}={n-1 \choose k-1}+{n-1 \choose k}[/latex]
edit: sad tek vidim da sam pomiješao lijevo-desno...
Rađeno je na vježbama 
Primjer iz glave (rađen baš na predavanju):
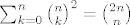
Desna strana: odabir n ljudi iz grupe od 2n ljudi.
Lijeva strana: prvo zanemariš sumu i gledaš kaj imaš. Pa se sjetiš simetrije binomnog koeficijenta pa imaš 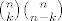
A to je odabir k ljudi (recimo dječaka) od njih n, i odabir n-k ljudi (recimo djevojčica) od njih n...kad sumiraš po svim k, dobije se baš broj odabira n ljudi iz grupe od 2n.
Trivijalan primjer:
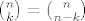
lijeva strana: odabir k ljudi od njih n.
desna strana: odabir n-k ljudi od njih n, a to je komplement od ovog prvog, pa je broj načina isti.
A dosta ih ide na foru nekakvog istaknutog člana...kad imaš na jednoj strani nešto, a na drugoj neka 2 člana pa između +.
Pa kažeš da je ovo lijevo (recimo) odabir k ljudi od n, a desno istaknemo neki član pa ako on je među odabranima, onda trebamo još k-1 od n-1, a ako nije onda trebamo još k od n-1. To je dokaz ovog:
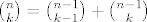
edit: sad tek vidim da sam pomiješao lijevo-desno...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy 
Zadnja promjena: Luuka; 11:50 uto, 27. 11. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
 Postano: 11:23 uto, 27. 11. 2007 Naslov: Postano: 11:23 uto, 27. 11. 2007 Naslov: |
    |
|
|
[quote="matmih"]Evo imam i ja pitanje, kako kombinatorno dokazat:
[latex] \sum_{i=0}^{r} {{n+i} \choose n}={{n+1+r} \choose n+1} [/latex][/quote]
s desne strane ti je izbor n+1 elemenata od njih n+r+1, i sad promatraj koji je najveći izabrani element... on može biti minimalno n+1, a maksimalno n+r+1... ak je on n+i+1 ( i ide od 0 do r), onda se preostalih n elemenata bira od njih n+i... i sad to sve sumiraš po i od 0 do r, i to ti je lijeva strana, i jednaka je desnoj :)
@luuka: imaš to na predavanjima... je da nije dokaz baš kombinatorni, al što ćeš :)
| matmih (napisa): | Evo imam i ja pitanje, kako kombinatorno dokazat:
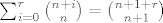 |
s desne strane ti je izbor n+1 elemenata od njih n+r+1, i sad promatraj koji je najveći izabrani element... on može biti minimalno n+1, a maksimalno n+r+1... ak je on n+i+1 ( i ide od 0 do r), onda se preostalih n elemenata bira od njih n+i... i sad to sve sumiraš po i od 0 do r, i to ti je lijeva strana, i jednaka je desnoj 
@luuka: imaš to na predavanjima... je da nije dokaz baš kombinatorni, al što ćeš 
_________________ kalendar 
  |
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 14:51 uto, 27. 11. 2007 Naslov: Postano: 14:51 uto, 27. 11. 2007 Naslov: |
    |
|
|
Prvo podijeliš sve sa 3^n pa dobiješ obične polinome i s jedne i s druge strane...pa možeš ili uvrštavat razne n-ove (mora vrijedit za svaki n pa si ti upikneš neke) , ili gledat članove uz potencije (2 polinoma su jednaka ako su pripadni koeficijenti jednaki)...
Prvo podijeliš sve sa 3^n pa dobiješ obične polinome i s jedne i s druge strane...pa možeš ili uvrštavat razne n-ove (mora vrijedit za svaki n pa si ti upikneš neke) , ili gledat članove uz potencije (2 polinoma su jednaka ako su pripadni koeficijenti jednaki)...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
amorphis
Forumaš(ica)


Pridružen/a: 10. 02. 2007. (23:15:13)
Postovi: (101)16
Lokacija: zg
|
 Postano: 15:15 uto, 27. 11. 2007 Naslov: Postano: 15:15 uto, 27. 11. 2007 Naslov: |
    |
|
|
tehnika rješavanja koju si napisala je ispravna, nakon uvrštavanja partikularnih rješenja u početnu rekurziju trebao bi se dobit izraz iz kojeg se preko istih potencija s lijeve i desne strane odrede konstante C&D, nakon toga se napiše konačno rješenja kao suma partikularnog i homogenog rješenja i onda se uvrste a0 i a1 da se odrede konstante A&B,
kad raspišem tvoju jednadžbu svi članovi koji imaju 'n' u sebi mi se pokrate i jedino što preživi je 18D-18, možda si krivo prepisala s ploče jer ako je rješenja cijelog izraza 3^n (a ne n*3^n) onda lako dobivaš da je D=1, kako je C i tako konstanta i pokrati se u izrazu mislim da ga se može uzet kao 0, dobiva se an=(A+Bn)3^n+n3^n, u to se uvrste početni uvjeti i dobiješ A=-B=2 odnosno an=(2-2n)3^n+n3^n
mislim da bi to trebalo bit u redu
tehnika rješavanja koju si napisala je ispravna, nakon uvrštavanja partikularnih rješenja u početnu rekurziju trebao bi se dobit izraz iz kojeg se preko istih potencija s lijeve i desne strane odrede konstante C&D, nakon toga se napiše konačno rješenja kao suma partikularnog i homogenog rješenja i onda se uvrste a0 i a1 da se odrede konstante A&B,
kad raspišem tvoju jednadžbu svi članovi koji imaju 'n' u sebi mi se pokrate i jedino što preživi je 18D-18, možda si krivo prepisala s ploče jer ako je rješenja cijelog izraza 3^n (a ne n*3^n) onda lako dobivaš da je D=1, kako je C i tako konstanta i pokrati se u izrazu mislim da ga se može uzet kao 0, dobiva se an=(A+Bn)3^n+n3^n, u to se uvrste početni uvjeti i dobiješ A=-B=2 odnosno an=(2-2n)3^n+n3^n
mislim da bi to trebalo bit u redu
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
j.b.i.n.s.h.
Forumaš(ica)

Pridružen/a: 24. 06. 2007. (10:28:11)
Postovi: (1B)16
|
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
|
















