| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 11:37 sub, 14. 1. 2006 Naslov: Molim vas, pomagajte Postano: 11:37 sub, 14. 1. 2006 Naslov: Molim vas, pomagajte |
    |
|
|
Da li mi netko može riješiti ove zadatke ili reći gdje mogu pronaći rješenja?
Zadaci su:
1. Ispitati da li je ([i]w[/i]+1)[i]w[/i]=[i]w[/i]^2 . (Ako nije obrazložiti, ako je pronaći odgovarajuću funkciju.)
2. Dokažite da je ([i]w[/i]+1)^2=[i]w[/i]^2+[i]w[/i]+1 .
3. Navedite primjer beskonačno potpuno uređenog skupa [i]A[/i] koji nije sličan skupu [b]N[/b], a ima ova svojstva:
a) [i]A[/i] ima najmaniji element, i
b) svaki element ima neposrednog sljedbenika, a svaki osim prvog ima i neposrednog prethodnika.
[size=18][/size][size=24][/size]
Da li mi netko može riješiti ove zadatke ili reći gdje mogu pronaći rješenja?
Zadaci su:
1. Ispitati da li je (w+1)w=w^2 . (Ako nije obrazložiti, ako je pronaći odgovarajuću funkciju.)
2. Dokažite da je (w+1)^2=w^2+w+1 .
3. Navedite primjer beskonačno potpuno uređenog skupa A koji nije sličan skupu N, a ima ova svojstva:
a) A ima najmaniji element, i
b) svaki element ima neposrednog sljedbenika, a svaki osim prvog ima i neposrednog prethodnika.
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 16:15 sub, 14. 1. 2006 Naslov: Re: Molim vas, pomagajte Postano: 16:15 sub, 14. 1. 2006 Naslov: Re: Molim vas, pomagajte |
    |
|
|
[quote]1. Ispitati da li je ([i]w[/i]+1)[i]w[/i]=[i]w[/i]^2 .[/quote]
Da.
Koristit ćemo [latex]1+\omega=\omega[/latex]
[latex](\omega+1)\omega=\sup_{n<\omega}(\omega+1)n=\\=\sup_{n<\omega}(\omega+1+\omega+1+\ldots+\omega+1)=\\=\sup_{n<\omega}(\omega+\omega+...+\omega+1)=\\=\sup_{n<\omega}(\omega\cdot n+1)=\omega^2[/latex]
jer je [latex]\omega\cdot n\leq\omega\cdot n+1\leq\omega\cdot(n+1)[/latex]
te [latex]\sup_{n<\omega}\omega\cdot n=\omega^2[/latex]
[quote]ako jest pronaći odgovarajuću funkciju[/quote]
Kakvu funkciju? Izomorfizam dvaju predstavnika tih rednih tipova?
Naprimjer
[latex](\omega+1)\times\omega\to\omega\times\omega[/latex]
je definirana ovako ([latex]n,k<\omega[/latex] proizvoljni):
[latex](n,0)\mapsto (n,0)\\
(\omega,k)\mapsto (1,k+1)\\
(n,k+1)\mapsto (n+1,k+1)[/latex]
[quote]2. Dokažite da je ([i]w[/i]+1)^2=[i]w[/i]^2+[i]w[/i]+1 .[/quote]
Zbog lijeve distributivnosti i prethodnog zadatka imamo:
[latex](\omega+1)(\omega+1)=(\omega+1)\omega+\omega+1=\omega^2+\omega+1[/latex]
[quote]3. Navedite primjer beskonačnog potpuno uređenog skupa [i]A[/i] koji nije sličan skupu [b]N[/b], a ima ova svojstva:
a) [i]A[/i] ima najmaniji element, i
b) svaki element ima neposrednog sljedbenika, a svaki osim prvog ima i neposrednog prethodnika.[/quote]
Na skupu [latex]\mathbb{N}\cup\mathbb{Z}[/latex] (disjunktna unija) definiramo uređaj tako da svaki element od [latex]\mathbb{N}[/latex] bude manji od svakog elementa od [latex]\mathbb{Z}[/latex], a uređaji na [latex]\mathbb{N}[/latex] i [latex]\mathbb{Z}[/latex] su uobičajeni.
Da pokušam predočiti grafički:
1 < 2 < 3 < ... < -3 < -2 < -1 < 0 < 1 < 2 < 3 < ...
| Citat: | | 1. Ispitati da li je (w+1)w=w^2 . |
Da.
Koristit ćemo 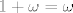
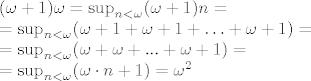
jer je 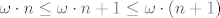
te 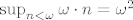
| Citat: | | ako jest pronaći odgovarajuću funkciju |
Kakvu funkciju? Izomorfizam dvaju predstavnika tih rednih tipova?
Naprimjer
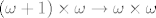
je definirana ovako (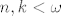 proizvoljni): proizvoljni):
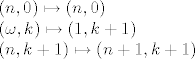
| Citat: | | 2. Dokažite da je (w+1)^2=w^2+w+1 . |
Zbog lijeve distributivnosti i prethodnog zadatka imamo:
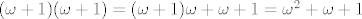
| Citat: | 3. Navedite primjer beskonačnog potpuno uređenog skupa A koji nije sličan skupu N, a ima ova svojstva:
a) A ima najmaniji element, i
b) svaki element ima neposrednog sljedbenika, a svaki osim prvog ima i neposrednog prethodnika. |
Na skupu 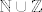 (disjunktna unija) definiramo uređaj tako da svaki element od (disjunktna unija) definiramo uređaj tako da svaki element od 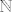 bude manji od svakog elementa od bude manji od svakog elementa od 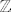 , a uređaji na , a uređaji na 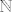 i i 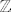 su uobičajeni. su uobičajeni.
Da pokušam predočiti grafički:
1 < 2 < 3 < ... < -3 < -2 < -1 < 0 < 1 < 2 < 3 < ...
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Boris Davidovič
Forumaš(ica)
Pridružen/a: 08. 01. 2004. (23:05:18)
Postovi: (3C)16
|
|
| [Vrh] |
|
|





