| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
 Postano: 23:47 uto, 15. 1. 2008 Naslov: Par zadataka o linearnoj nezavisnosti nekih skupova Postano: 23:47 uto, 15. 1. 2008 Naslov: Par zadataka o linearnoj nezavisnosti nekih skupova |
    |
|
|
Zadatak glasi:
Trigonometrijskim polinomom zovemo linearnu kombinaciju funkcija [latex]e^{ikt} (k\in\mathbb{Z}, t\in\mathbb{R})[/latex].
Dokažite da je svaki skup linearno nezavisnih trigonometrijskih polinoma konačan ili prebrojiv.
E pa sad, ja sam to probao ovako, uzmem neki neprebrojivi skup linearno nezavisnih trigonometrijskih polinoma (nemam pojma kako da to zapišem) i uzmem njihovu linearnu kombinaciju. I sad grupiram koeficijente po funkcijama [latex]e^{ikt} (k\in\mathbb{Z}, t\in\mathbb{R})[/latex] i pošto su one nezavisne, ono što je uz njih izjednačim s 0. E sad imam prebrojivo mnogo jednadžbi s neprebrojivo mnogo nepoznanica i kažem da to nema jedinstveno rješenje (naravno ne znam to dokazat) i da ti polinomi ne mogu biti linearno nezavisni. Jel se može to tako?
Drugo moje pitanje glasi kako dokazati da su funkcije [latex]e^{ikt} (k\in\mathbb{Z}, t\in\mathbb{R})[/latex] nezavisne?
Ja sam uzeo n tih funkcija i izjednačio njihovu linearnu kombinaciju s 0 i sad dobijem da vrijedi [latex]a_0+a_1cost+...+a_ncos(nt)=0[/latex] i [latex]a_1sint+...+a_nsin(nt)=0[/latex]. Sad pošto to vrijedi za svaki t, moj argument je opet imam neprebrojivo mnogo jednadžbi s prebrojivo mnogo nepoznanica i to ima jedinstveno rješenje (opet ne znam zašto), a to je da su svi koeficijenti 0. Jel to išto valja?
Svima koji se upuste u rasvjetljavanje ovog slučaja, unaprijed se zahvaljujem.
Zadatak glasi:
Trigonometrijskim polinomom zovemo linearnu kombinaciju funkcija 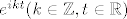 . .
Dokažite da je svaki skup linearno nezavisnih trigonometrijskih polinoma konačan ili prebrojiv.
E pa sad, ja sam to probao ovako, uzmem neki neprebrojivi skup linearno nezavisnih trigonometrijskih polinoma (nemam pojma kako da to zapišem) i uzmem njihovu linearnu kombinaciju. I sad grupiram koeficijente po funkcijama 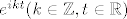 i pošto su one nezavisne, ono što je uz njih izjednačim s 0. E sad imam prebrojivo mnogo jednadžbi s neprebrojivo mnogo nepoznanica i kažem da to nema jedinstveno rješenje (naravno ne znam to dokazat) i da ti polinomi ne mogu biti linearno nezavisni. Jel se može to tako? i pošto su one nezavisne, ono što je uz njih izjednačim s 0. E sad imam prebrojivo mnogo jednadžbi s neprebrojivo mnogo nepoznanica i kažem da to nema jedinstveno rješenje (naravno ne znam to dokazat) i da ti polinomi ne mogu biti linearno nezavisni. Jel se može to tako?
Drugo moje pitanje glasi kako dokazati da su funkcije 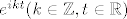 nezavisne? nezavisne?
Ja sam uzeo n tih funkcija i izjednačio njihovu linearnu kombinaciju s 0 i sad dobijem da vrijedi 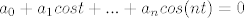 i i 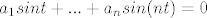 . Sad pošto to vrijedi za svaki t, moj argument je opet imam neprebrojivo mnogo jednadžbi s prebrojivo mnogo nepoznanica i to ima jedinstveno rješenje (opet ne znam zašto), a to je da su svi koeficijenti 0. Jel to išto valja? . Sad pošto to vrijedi za svaki t, moj argument je opet imam neprebrojivo mnogo jednadžbi s prebrojivo mnogo nepoznanica i to ima jedinstveno rješenje (opet ne znam zašto), a to je da su svi koeficijenti 0. Jel to išto valja?
Svima koji se upuste u rasvjetljavanje ovog slučaja, unaprijed se zahvaljujem.
|
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 10:03 sri, 16. 1. 2008 Naslov: Re: Par zadataka o linearnoj nezavisnosti nekih skupova Postano: 10:03 sri, 16. 1. 2008 Naslov: Re: Par zadataka o linearnoj nezavisnosti nekih skupova |
    |
|
|
[quote="Silver Surfer"]
Drugo moje pitanje glasi kako dokazati da su funkcije [latex]e^{ikt} (k\in\mathbb{Z}, t\in\mathbb{R})[/latex] nezavisne?
[/quote]
Evo ja cu samo jedno... , uzmi linearnu kombinaciju [latex]\sum_{k=1}^{n}\alpha_k e^{ikt}[/latex]. Pomnoži sa [latex]e^{imt},1\leq m\leq n[/latex], te integriraj po nekom pogodnom intervalu, npr [latex] [-\pi,\pi][/latex]. Dakle, [latex](e^{ikt})_{k\in\mathbb{N}}[/latex] je ortogonalna baza u prostoru [latex]C([-\pi,\pi])[/latex]. Cak jos vise, ako normiras svaku od tih fija ( u odnosu na [latex]\|\cdot\|_2[/latex] normu) taj skup je ortonormirana baza.
| Silver Surfer (napisa): |
Drugo moje pitanje glasi kako dokazati da su funkcije 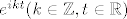 nezavisne? nezavisne?
|
Evo ja cu samo jedno... , uzmi linearnu kombinaciju 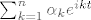 . Pomnoži sa . Pomnoži sa 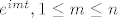 , te integriraj po nekom pogodnom intervalu, npr , te integriraj po nekom pogodnom intervalu, npr 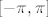 . Dakle, . Dakle, 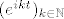 je ortogonalna baza u prostoru je ortogonalna baza u prostoru 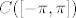 . Cak jos vise, ako normiras svaku od tih fija ( u odnosu na . Cak jos vise, ako normiras svaku od tih fija ( u odnosu na  normu) taj skup je ortonormirana baza. normu) taj skup je ortonormirana baza.
|
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
 Postano: 1:39 sub, 19. 1. 2008 Naslov: Re: Par zadataka o linearnoj nezavisnosti nekih skupova Postano: 1:39 sub, 19. 1. 2008 Naslov: Re: Par zadataka o linearnoj nezavisnosti nekih skupova |
    |
|
|
[quote="Mr.Doe"][quote="Silver Surfer"]
Drugo moje pitanje glasi kako dokazati da su funkcije [latex]e^{ikt} (k\in\mathbb{Z}, t\in\mathbb{R})[/latex] nezavisne?
[/quote]
Evo ja cu samo jedno... , uzmi linearnu kombinaciju [latex]\sum_{k=1}^{n}\alpha_k e^{ikt}[/latex]. Pomnoži sa [latex]e^{imt},1\leq m\leq n[/latex], te integriraj po nekom pogodnom intervalu, npr [latex] [-\pi,\pi][/latex]. Dakle, [latex](e^{ikt})_{k\in\mathbb{N}}[/latex] je ortogonalna baza u prostoru [latex]C([-\pi,\pi])[/latex]. Cak jos vise, ako normiras svaku od tih fija ( u odnosu na [latex]\|\cdot\|_2[/latex] normu) taj skup je ortonormirana baza.[/quote]
Prvo, ja to bas ne znam integrirat (jel mozes raspisat malo?), pa ne vidim sto se time dobije. :oops: A drugo, kako je to moguce? Sto se to ne kosi s ovim drugim zadatkom sto sam napisao? Ako je [latex](e^{ikt})_{k\in\mathbb{N}}[/latex] baza za [latex]C([-\pi,\pi])[/latex] onda po tom zadatku mora biti neprebrojiva, a ona je ocito prebrojiva! :o
| Mr.Doe (napisa): | | Silver Surfer (napisa): |
Drugo moje pitanje glasi kako dokazati da su funkcije 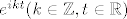 nezavisne? nezavisne?
|
Evo ja cu samo jedno... , uzmi linearnu kombinaciju 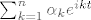 . Pomnoži sa . Pomnoži sa 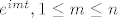 , te integriraj po nekom pogodnom intervalu, npr , te integriraj po nekom pogodnom intervalu, npr 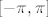 . Dakle, . Dakle, 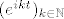 je ortogonalna baza u prostoru je ortogonalna baza u prostoru 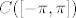 . Cak jos vise, ako normiras svaku od tih fija ( u odnosu na . Cak jos vise, ako normiras svaku od tih fija ( u odnosu na  normu) taj skup je ortonormirana baza. normu) taj skup je ortonormirana baza. |
Prvo, ja to bas ne znam integrirat (jel mozes raspisat malo?), pa ne vidim sto se time dobije.  A drugo, kako je to moguce? Sto se to ne kosi s ovim drugim zadatkom sto sam napisao? Ako je A drugo, kako je to moguce? Sto se to ne kosi s ovim drugim zadatkom sto sam napisao? Ako je 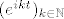 baza za baza za 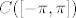 onda po tom zadatku mora biti neprebrojiva, a ona je ocito prebrojiva! onda po tom zadatku mora biti neprebrojiva, a ona je ocito prebrojiva! 
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 13:50 sub, 19. 1. 2008 Naslov: Re: Par zadataka o linearnoj nezavisnosti nekih skupova Postano: 13:50 sub, 19. 1. 2008 Naslov: Re: Par zadataka o linearnoj nezavisnosti nekih skupova |
    |
|
|
[quote="Silver Surfer"]
Prvo, ja to bas ne znam integrirat (jel mozes raspisat malo?), pa ne vidim sto se time dobije. :oops: [/quote]
Upucujem te na skriptu prof. Guljas Matematicka analiza 1 & 2. http://web.math.hr/nastava/analiza/files/MATANALuR.pdf , stranica 171.
[quote="Silver Surfer"]
A drugo, kako je to moguce? Sto se to ne kosi s ovim drugim zadatkom sto sam napisao? Ako je [latex](e^{ikt})_{\underline{k\in\mathbb{N}}}[/latex] baza za [latex]C([-\pi,\pi])[/latex] onda po tom zadatku mora biti neprebrojiva, a ona je ocito prebrojiva! :o[/quote]
Prvo, imas prebrojivo mnogo elemenata (koji su kandidati za bazu), stoga ne razumijem kako si dosao do toga da je neprebrojiva. Takoder mislim da si se zaletio sa zadatkom, tj. da nisi imao na umu prostor za koji nalazis bazu ( u ovom slucaj je to [latex]C([-\pi,\pi])[/latex] ), pa cak ni ("prirodnu") normu za taj prostor.
Takoder, kada govoris o lin. kombinaciji, onda se misli na konacnu sumu elemenata, ukoliko imas neprebrojivu sumu onda bi to bilo [latex]\displaystyle\sup_{\mathcal{K}\subseteq\mathcal{F},\mathcal{K}\textrm{konacan}}\{\sum_{k\in\mathcal{K},}\alpha_{k}x_k\}[/latex] , gdje je [latex]\mathcal{F}[/latex] indeksni skup.
No, mislim da dalje od toga neces doci.
| Silver Surfer (napisa): |
Prvo, ja to bas ne znam integrirat (jel mozes raspisat malo?), pa ne vidim sto se time dobije.  |
Upucujem te na skriptu prof. Guljas Matematicka analiza 1 & 2. http://web.math.hr/nastava/analiza/files/MATANALuR.pdf , stranica 171.
| Silver Surfer (napisa): |
A drugo, kako je to moguce? Sto se to ne kosi s ovim drugim zadatkom sto sam napisao? Ako je 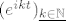 baza za baza za 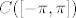 onda po tom zadatku mora biti neprebrojiva, a ona je ocito prebrojiva! onda po tom zadatku mora biti neprebrojiva, a ona je ocito prebrojiva!  |
Prvo, imas prebrojivo mnogo elemenata (koji su kandidati za bazu), stoga ne razumijem kako si dosao do toga da je neprebrojiva. Takoder mislim da si se zaletio sa zadatkom, tj. da nisi imao na umu prostor za koji nalazis bazu ( u ovom slucaj je to 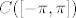 ), pa cak ni ("prirodnu") normu za taj prostor. ), pa cak ni ("prirodnu") normu za taj prostor.
Takoder, kada govoris o lin. kombinaciji, onda se misli na konacnu sumu elemenata, ukoliko imas neprebrojivu sumu onda bi to bilo 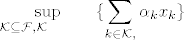 , gdje je , gdje je 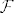 indeksni skup. indeksni skup.
No, mislim da dalje od toga neces doci.
|
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 15:11 pon, 21. 1. 2008 Naslov: Postano: 15:11 pon, 21. 1. 2008 Naslov: |
    |
|
|
Dobro je zadan zadatak, ono sto kolega nije imao na umu jest da, na beskonacno dim. prostoru [latex]X[/latex], [latex]span(\{x_n\}_{n\in\mathbb{N}})\neq X[/latex], nego [latex]\overline{span(\{x_n\}_{n\in\mathbb{N}})}= X[/latex] .
Takoder kolega ne razlikuje/razumije pojmove baze i skupa koji razapinje beskonacno dim. vekt. prostor. Svi zadaci koje je kolega naveo su, iz knjige prof. Kurepe: konacno dim. vek. prostori i primjene.
Dobro je zadan zadatak, ono sto kolega nije imao na umu jest da, na beskonacno dim. prostoru  , , 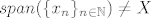 , nego , nego 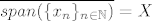 . .
Takoder kolega ne razlikuje/razumije pojmove baze i skupa koji razapinje beskonacno dim. vekt. prostor. Svi zadaci koje je kolega naveo su, iz knjige prof. Kurepe: konacno dim. vek. prostori i primjene.
|
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
|
| [Vrh] |
|
|





