| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
k8yvis
Forumaš(ica)

Pridružen/a: 13. 10. 2006. (14:32:30)
Postovi: (79)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 15:06 sri, 6. 2. 2008 Naslov: Postano: 15:06 sri, 6. 2. 2008 Naslov: |
    |
|
|
Ta točka (nazovimo je x0) je nultočka i zadanog polinoma, i njegove derivacije. A pošto je cjelobrojna onda x0|a (nultočka dijeli slobodan član) dakle x0=ka za neki k. Sad to ubaciš u polinom, i u njegovu derivaciju, malo sredi i to je to. (moguće da neće ni trebat x0=ka) a se javlja samo u slobodnom članu pa će nestat kad deriviraš. A polinomu 3.stupnja znaš pogodit nultočku (opet gledaš slobodan član)
Ta točka (nazovimo je x0) je nultočka i zadanog polinoma, i njegove derivacije. A pošto je cjelobrojna onda x0|a (nultočka dijeli slobodan član) dakle x0=ka za neki k. Sad to ubaciš u polinom, i u njegovu derivaciju, malo sredi i to je to. (moguće da neće ni trebat x0=ka) a se javlja samo u slobodnom članu pa će nestat kad deriviraš. A polinomu 3.stupnja znaš pogodit nultočku (opet gledaš slobodan član)
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 16:18 sri, 6. 2. 2008 Naslov: Postano: 16:18 sri, 6. 2. 2008 Naslov: |
    |
|
|
Hm, kad mi je bio zadan [latex]p(x)=x^3+ax+b[/latex], a zna se da je jedna nultočka -2, a druga je dvostruka, te se traže a i b, sam zapisao ovako:
[latex]p(x)=(x-\alpha)^2(x-2)[/latex]
Na istom principu sam riješio (skoro pa :roll: ) 9. zadatak, gdje se traži 2 dvostruke od polinoma četvrtog stupnja:
[latex]p(x)=(x-\alpha)^2(x-\beta)^2[/latex]
E sad se ovdje traži jedna dvostruka od polinoma stupnja 4.
Da li je to onda:
[latex]p(x)=(x-\alpha)^2(x-0)^2[/latex]?
Hm, kad mi je bio zadan 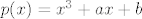 , a zna se da je jedna nultočka -2, a druga je dvostruka, te se traže a i b, sam zapisao ovako: , a zna se da je jedna nultočka -2, a druga je dvostruka, te se traže a i b, sam zapisao ovako:

Na istom principu sam riješio (skoro pa  ) 9. zadatak, gdje se traži 2 dvostruke od polinoma četvrtog stupnja: ) 9. zadatak, gdje se traži 2 dvostruke od polinoma četvrtog stupnja:
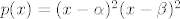
E sad se ovdje traži jedna dvostruka od polinoma stupnja 4.
Da li je to onda:
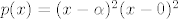 ? ?
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 16:27 sri, 6. 2. 2008 Naslov: Postano: 16:27 sri, 6. 2. 2008 Naslov: |
    |
|
|
[quote="punio4"]Hm, kad mi je bio zadan [latex]p(x)=x^3+ax+b[/latex], a zna se da je jedna nultočka -2, a druga je dvostruka, te se traže a i b, sam zapisao ovako:
[latex]p(x)=(x-\alpha)^2(x-2)[/latex][/quote]
ako je -2 nultočka onda mora biti: [latex]p(x)=(x-\alpha)^2(x+2)[/latex]
[quote="punio4"]Na istom principu sam riješio (skoro pa :roll: ) 9. zadatak, gdje se traži 2 dvostruke od polinoma četvrtog stupnja:
[latex]p(x)=(x-\alpha)^2(x-\beta)^2[/latex]
E sad se ovdje traži jedna dvostruka od polinoma stupnja 4.
Da li je to onda:
[latex]p(x)=(x-\alpha)^2(x-0)^2[/latex]?[/quote]
pa ne. tu su ti [latex]\alpha[/latex] i 0 dvostruke, kao što si i napisao. :?
ovako: [latex]p(x)=(x-\alpha)^2(x-\beta)(x-\gamma)[/latex], općenito, naravno :)
| punio4 (napisa): | Hm, kad mi je bio zadan 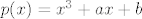 , a zna se da je jedna nultočka -2, a druga je dvostruka, te se traže a i b, sam zapisao ovako: , a zna se da je jedna nultočka -2, a druga je dvostruka, te se traže a i b, sam zapisao ovako:
 |
ako je -2 nultočka onda mora biti: 
| punio4 (napisa): | Na istom principu sam riješio (skoro pa  ) 9. zadatak, gdje se traži 2 dvostruke od polinoma četvrtog stupnja: ) 9. zadatak, gdje se traži 2 dvostruke od polinoma četvrtog stupnja:
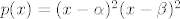
E sad se ovdje traži jedna dvostruka od polinoma stupnja 4.
Da li je to onda:
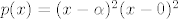 ? ? |
pa ne. tu su ti  i 0 dvostruke, kao što si i napisao. i 0 dvostruke, kao što si i napisao. 
ovako: 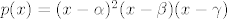 , općenito, naravno , općenito, naravno 
_________________
ima let u finish
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 16:31 sri, 6. 2. 2008 Naslov: Postano: 16:31 sri, 6. 2. 2008 Naslov: |
    |
|
|
[quote="ma"][quote="punio4"]Hm, kad mi je bio zadan [latex]p(x)=x^3+ax+b[/latex], a zna se da je jedna nultočka -2, a druga je dvostruka, te se traže a i b, sam zapisao ovako:
[latex]p(x)=(x-\alpha)^2(x-2)[/latex][/quote]
ako je -2 nultočka onda mora biti: [latex]p(x)=(x-\alpha)^2(x+2)[/latex]
[quote="punio4"]Na istom principu sam riješio (skoro pa :roll: ) 9. zadatak, gdje se traži 2 dvostruke od polinoma četvrtog stupnja:
[latex]p(x)=(x-\alpha)^2(x-\beta)^2[/latex]
E sad se ovdje traži jedna dvostruka od polinoma stupnja 4.
Da li je to onda:
[latex]p(x)=(x-\alpha)^2(x-0)^2[/latex]?[/quote]
pa ne. tu su ti [latex]\alpha[/latex] i 0 dvostruke, kao što si i napisao. :?
ovako: [latex]p(x)=(x-\alpha)^2(x-\beta)(x-\gamma)[/latex], općenito, naravno :)[/quote]
Ono prvo sam krivo prepisao... Jedna nultočka je 2.
Ovo drugo... Glupa logika :P Kao, ako je nula onda znači da nema.
Pokušavam si nekako lakše zapamtiti, vizualno. mrzim polinome.
Ako ima jednu dvostruku nultočku, onda samo negdje mora biti [latex]\alpha^2[/latex]... Po nekoj mojoj logici.. Kako to zapisati faktorizirano? Ili se ne može ta jedna nultočka izraziti samo pomoću [latex]\alpha[/latex]
| ma (napisa): | | punio4 (napisa): | Hm, kad mi je bio zadan 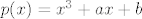 , a zna se da je jedna nultočka -2, a druga je dvostruka, te se traže a i b, sam zapisao ovako: , a zna se da je jedna nultočka -2, a druga je dvostruka, te se traže a i b, sam zapisao ovako:
 |
ako je -2 nultočka onda mora biti: 
| punio4 (napisa): | Na istom principu sam riješio (skoro pa  ) 9. zadatak, gdje se traži 2 dvostruke od polinoma četvrtog stupnja: ) 9. zadatak, gdje se traži 2 dvostruke od polinoma četvrtog stupnja:
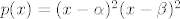
E sad se ovdje traži jedna dvostruka od polinoma stupnja 4.
Da li je to onda:
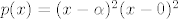 ? ? |
pa ne. tu su ti  i 0 dvostruke, kao što si i napisao. i 0 dvostruke, kao što si i napisao. 
ovako: 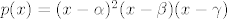 , općenito, naravno , općenito, naravno  |
Ono prvo sam krivo prepisao... Jedna nultočka je 2.
Ovo drugo... Glupa logika  Kao, ako je nula onda znači da nema. Kao, ako je nula onda znači da nema.
Pokušavam si nekako lakše zapamtiti, vizualno. mrzim polinome.
Ako ima jednu dvostruku nultočku, onda samo negdje mora biti 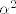 ... Po nekoj mojoj logici.. Kako to zapisati faktorizirano? Ili se ne može ta jedna nultočka izraziti samo pomoću ... Po nekoj mojoj logici.. Kako to zapisati faktorizirano? Ili se ne može ta jedna nultočka izraziti samo pomoću 
Zadnja promjena: punio4; 16:35 sri, 6. 2. 2008; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
yimpa
Forumaš(ica)
Pridružen/a: 18. 01. 2008. (23:56:37)
Postovi: (26)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 21:01 sri, 6. 2. 2008 Naslov: Postano: 21:01 sri, 6. 2. 2008 Naslov: |
    |
|
|
Pretpostavi suprotno ;)
Postoji racionalna nultočka, x0=m/k , M(m,n)=1 (dakle potpuno skraćen razlomak)
p(x0)=m^n/k^n - 7 =0
(m/k)^n = 7
m/k = nti korijen iz 7 ,
m = k * nti korijen (7) a to nije iz Z za nijedne k,m iz Z
Valjda tako
Pretpostavi suprotno 
Postoji racionalna nultočka, x0=m/k , M(m,n)=1 (dakle potpuno skraćen razlomak)
p(x0)=m^n/k^n - 7 =0
(m/k)^n = 7
m/k = nti korijen iz 7 ,
m = k * nti korijen (7) a to nije iz Z za nijedne k,m iz Z
Valjda tako
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
k8yvis
Forumaš(ica)

Pridružen/a: 13. 10. 2006. (14:32:30)
Postovi: (79)16
Spol: 
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
|





















