Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

Zna li neko rješiti
WWW:

Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 2. godine -> Vjerojatnost
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
Dino
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 12. 02. 2008. (21:27:34)
Postovi: (2)16
Sarma = la pohva - posuda
0 = 0 - 0
PostPostano: 21:37 uto, 12. 2. 2008    Naslov: Zna li neko rješiti Citirajte i odgovorite
Pretpostavimo da u kutiji imamo 6 novčića: 1 pravedan (pismo-glava), 2 nova sa 2 glave i 3 novčića sa 2 pisma. Izvadimo nasumice novčić iz kutije i bacamo ga 3 puta. Ako dobijemo glavu sva 3 puta koja je vjerovatnoća da je novčić bio pravedan?
Pretpostavimo da u kutiji imamo 6 novčića: 1 pravedan (pismo-glava), 2 nova sa 2 glave i 3 novčića sa 2 pisma. Izvadimo nasumice novčić iz kutije i bacamo ga 3 puta. Ako dobijemo glavu sva 3 puta koja je vjerovatnoća da je novčić bio pravedan?


[Vrh]
Korisnički profil Pošaljite privatnu poruku
ma
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: muško
Sarma = la pohva - posuda
58 = 89 - 31
PostPostano: 22:00 uto, 12. 2. 2008    Naslov: Re: Zna li neko rješiti Citirajte i odgovorite
[quote="Dino"]Pretpostavimo da u kutiji imamo 6 novčića: 1 pravedan (pismo-glava), 2 nova sa 2 glave i 3 novčića sa 2 pisma. Izvadimo nasumice novčić iz kutije i bacamo ga 3 puta. Ako dobijemo glavu sva 3 puta koja je vjerovatnoća da je novčić bio pravedan?[/quote]

definiraš potpun sistem događaja:
H1:={izvukli smo pravedni novčić},
H2:={izvukli smo novčić s 2 glave},
H3:={izvukli smo novčić s 2 pisma}.

znamo:
[latex]P(H_1)=\frac{1}{6},
P(H_2)=\frac{1}{3},
P(H_3)=\frac{1}{2}.[/latex]

ako je A={pri bacanju smo dobili tri glave}, tada nas zanima [latex]P(H_1|A)[/latex].

vrijedi: [latex]P(H_1|A)=\frac{P(A|H_1) \cdot P(H_1)}{P(A|H_1) \cdot P(H_1) + P(A|H_2) \cdot P(H_2) + P(A|H_3) \cdot P(H_3)}[/latex]

znamo:
[latex]P(A|H_1)=(\frac{1}{2})^3,
P(A|H_2)=1,
P(A|H_3)=0.[/latex]

uvrstimo:
[latex]P(H_1|A)=\frac{\frac{1}{8} \cdot \frac{1}{6}}{\frac{1}{8} \cdot \frac{1}{6} + 1 \cdot \frac{1}{3} + 0 \cdot \frac{1}{2}} \approx 0.0588235294117[/latex]

iskreno se nadam da je točno - nakon ovoliko muke s latexom. :rakun:
Dino (napisa):
Pretpostavimo da u kutiji imamo 6 novčića: 1 pravedan (pismo-glava), 2 nova sa 2 glave i 3 novčića sa 2 pisma. Izvadimo nasumice novčić iz kutije i bacamo ga 3 puta. Ako dobijemo glavu sva 3 puta koja je vjerovatnoća da je novčić bio pravedan?


definiraš potpun sistem događaja:
H1:={izvukli smo pravedni novčić},
H2:={izvukli smo novčić s 2 glave},
H3:={izvukli smo novčić s 2 pisma}.

znamo:


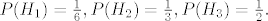
ako je A={pri bacanju smo dobili tri glave}, tada nas zanima .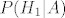

vrijedi: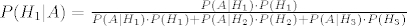

znamo:


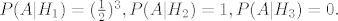
uvrstimo:


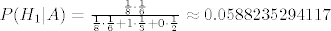
iskreno se nadam da je točno - nakon ovoliko muke s latexom. Rakun Koji Pleshe



_________________
ima let u finish
[Vrh]
Korisnički profil Pošaljite privatnu poruku
matmih
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: muško
Sarma = la pohva - posuda
36 = 51 - 15
Lokacija: {Zg, De , Ri}
PostPostano: 22:05 uto, 12. 2. 2008    Naslov: Citirajte i odgovorite
Ja bi reko da je točno jer je tolko i meni došlo, al opet to je vjerojatnost. :lol:
Ja bi reko da je točno jer je tolko i meni došlo, al opet to je vjerojatnost. Laughing


[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
ma
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: muško
Sarma = la pohva - posuda
58 = 89 - 31
PostPostano: 22:08 uto, 12. 2. 2008    Naslov: Citirajte i odgovorite
[quote="matmih"]Ja bi reko da je točno jer je tolko i meni došlo, al opet to je vjerojatnost. :lol:[/quote]

da. valja izračunati vjerojatnost da ti je rješenje točno. :?


:swing:
matmih (napisa):
Ja bi reko da je točno jer je tolko i meni došlo, al opet to je vjerojatnost. Laughing


da. valja izračunati vjerojatnost da ti je rješenje točno. Confused


Ljuljacka



_________________
ima let u finish
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Dino
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 12. 02. 2008. (21:27:34)
Postovi: (2)16
Sarma = la pohva - posuda
0 = 0 - 0
PostPostano: 22:09 uto, 12. 2. 2008    Naslov: Citirajte i odgovorite
Hvala najljepša :lol:
Hvala najljepša Laughing


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 2. godine -> Vjerojatnost Vremenska zona: GMT + 01:00.
Stranica 1 / 1.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan