| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
ivica13
Forumaš(ica)

Pridružen/a: 03. 10. 2007. (14:01:02)
Postovi: (102)16
Spol: 
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
BitterSweet
Forumaš(ica)


Pridružen/a: 10. 10. 2007. (21:09:28)
Postovi: (174)16
Spol: 
Lokacija: sjeverno od raja
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
BitterSweet
Forumaš(ica)


Pridružen/a: 10. 10. 2007. (21:09:28)
Postovi: (174)16
Spol: 
Lokacija: sjeverno od raja
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 17:51 sri, 28. 11. 2007 Naslov: Postano: 17:51 sri, 28. 11. 2007 Naslov: |
    |
|
|
Imam jedan problem.
Jasno mi je rješavat, reducirat, tražit sume i presjeke kad imam neke konkretne vektore, recimo [latex]M=\{(1,0),(0,1)\}[/latex].
Evo, recimo 1. zadatak iz dz:
Dokažite da je [latex]M=\{(x_1, x_2, x_3, x_4) \in \mathbb{R}^4 : 2x_1+x_2+x_3-x_4=0, x_1-x_2=0\}[/latex] potprostor od [latex]\mathbb{R}^4[/latex] te mu odredite jednu bazu i dimenziju.
Nije mi jasno što je taj [latex](x_1, x_2, x_3, x_4)[/latex].
Je li to skup od 4 vektora? Jedan vektor sa 4 elementa? Ako su 4 vektora, koliko svaki ima elemenata?
Ako itko može malo pojasnit, nek pliz pomogne.
Imam jedan problem.
Jasno mi je rješavat, reducirat, tražit sume i presjeke kad imam neke konkretne vektore, recimo 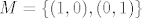 . .
Evo, recimo 1. zadatak iz dz:
Dokažite da je 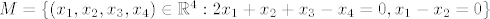 potprostor od potprostor od 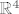 te mu odredite jednu bazu i dimenziju. te mu odredite jednu bazu i dimenziju.
Nije mi jasno što je taj 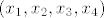 . .
Je li to skup od 4 vektora? Jedan vektor sa 4 elementa? Ako su 4 vektora, koliko svaki ima elemenata?
Ako itko može malo pojasnit, nek pliz pomogne.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
 Postano: 18:05 sri, 28. 11. 2007 Naslov: Postano: 18:05 sri, 28. 11. 2007 Naslov: |
    |
|
|
Eh, vidi se da nema asistentice Valent!
Dakle M ti je skup svih vektora iz [latex] \mathbb{R}^4 [/latex] sa svojstvom koje si naveo.
Svaki vektor iz [latex] \mathbb{R}^4 [/latex] se sastoji od 4 komponente, dakle [latex] v\in \mathbb{R}^4[/latex] tada je v oblika [latex] v=(x_1,x_2,x_3,x_4) [/latex].
Kada bi recimo bilo [latex] v\in \mathbb{R}^2, v=(x_1,x_2) [/latex].
Nadam se da je jasnije.
Općenito [latex] (x_1,x_2,x_3,x_4) [/latex] je [b]uređena[/b] četvorka, različito od skupa [latex] \left\{x_1,x_2,x_3,x_4\right\} [/latex]
Eh, vidi se da nema asistentice Valent!
Dakle M ti je skup svih vektora iz 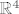 sa svojstvom koje si naveo. sa svojstvom koje si naveo.
Svaki vektor iz 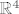 se sastoji od 4 komponente, dakle se sastoji od 4 komponente, dakle  tada je v oblika tada je v oblika 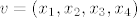 . .
Kada bi recimo bilo 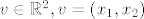 . .
Nadam se da je jasnije.
Općenito 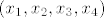 je uređena četvorka, različito od skupa je uređena četvorka, različito od skupa 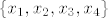
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:26 sri, 28. 11. 2007 Naslov: Postano: 18:26 sri, 28. 11. 2007 Naslov: |
    |
|
|
Da, parametarsko rješenje...dobije se:
[latex]x_{2}=x_{1}
x_{3}=-3x_{1}+x_{4}[/latex]
pa je [latex]x=(x_{1},x_{2},x_{3},x_{4})= (x_{1},x_{1},-3x_{1}+x_{4},x_{4}) = x_{1} (1,1,-3,0) + x_{4} (0,0,1,1) [/latex].
Sad je [latex][\{ (1,1,-3,0),(0,0,1,1)\}][/latex] skup izvodnica za M (svaki vektor iz M se može prikazat kao lin komb ta 2), to je lin nezavisno (očito se vidi- zadnja koordinata) pa je to i baza za M.
Naravno, baza nije jedinstveno određena, ovo je samo jedna od opcija :wink:
A da je M potprostor pokažeš da je ax+by iz M za sve a,b iz R i x,y iz M.
edit: zaboravih napisat malu sitnicu: x1,x4 iz R proizvoljni... :oops:
Da, parametarsko rješenje...dobije se:
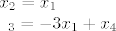
pa je 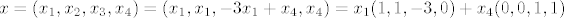 . .
Sad je 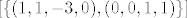 skup izvodnica za M (svaki vektor iz M se može prikazat kao lin komb ta 2), to je lin nezavisno (očito se vidi- zadnja koordinata) pa je to i baza za M. skup izvodnica za M (svaki vektor iz M se može prikazat kao lin komb ta 2), to je lin nezavisno (očito se vidi- zadnja koordinata) pa je to i baza za M.
Naravno, baza nije jedinstveno određena, ovo je samo jedna od opcija 
A da je M potprostor pokažeš da je ax+by iz M za sve a,b iz R i x,y iz M.
edit: zaboravih napisat malu sitnicu: x1,x4 iz R proizvoljni... 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy 
Zadnja promjena: Luuka; 18:46 sri, 28. 11. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
 Postano: 18:31 sri, 28. 11. 2007 Naslov: Postano: 18:31 sri, 28. 11. 2007 Naslov: |
    |
|
|
Ovo si dobro napisao sada još izrazi recimo: [latex] x_3=-3x_1+x_4, x_1,x_4\in \mathbb{R} [/latex] proizvoljni.
Šta to sada znači?
To znači: ako nam je vektor v [latex] v=(x_1,x_2,x_3,x_4) [/latex] iz M onda je on oblika:
[latex] (x_1,x_1,-3x_1+x_4,x_4) [/latex].
Sada imamo:
[latex]x_1(1,1,-3,0)+x_4(0,0,1,1) [/latex] i vektori
[latex] (1,1,-3,0),(0,0,1,1,) [/latex] čine s.i za M.
Očito su linearno nezavisni i čine bazu za M, dim M=2.
Prije toga moraš dokazat da je M potprostor, a to je standard, uzmemo dva vektora iz M i pokažemo da je njihova lin. kombinacija opet u M. To je već riješeno na više mjesta.
Ovo si dobro napisao sada još izrazi recimo: 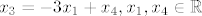 proizvoljni. proizvoljni.
Šta to sada znači?
To znači: ako nam je vektor v 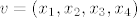 iz M onda je on oblika: iz M onda je on oblika:
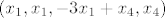 . .
Sada imamo:
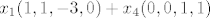 i vektori i vektori
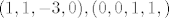 čine s.i za M. čine s.i za M.
Očito su linearno nezavisni i čine bazu za M, dim M=2.
Prije toga moraš dokazat da je M potprostor, a to je standard, uzmemo dva vektora iz M i pokažemo da je njihova lin. kombinacija opet u M. To je već riješeno na više mjesta.
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 20:08 sri, 28. 11. 2007 Naslov: Postano: 20:08 sri, 28. 11. 2007 Naslov: |
    |
|
|
edit: napiso sam glupost prije...
Matrica ti treba bit iz M2(C) pa su ti njeni elementi komplexni, tebi su realni...
edit: napiso sam glupost prije...
Matrica ti treba bit iz M2(C) pa su ti njeni elementi komplexni, tebi su realni...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
|




















