[quote="punio4"]Ako pokazujemo da je unutar intervala epsilon, kako i zašto se pojavilo ovo M + |b| ?[/quote]
Zbog naštimavanja za provjeravanje konvergencije od [latex](a_n \cdot b_n)_{n \in \mathbb{N}}.[/latex]
Niz [latex](a_n)[/latex] (analogno za niz [latex](b_n)[/latex]) je konvergentan pa za svaki pozitivan [latex]\varepsilon[/latex] postoji [latex]n_{\varepsilon} \in \mathbb{N}[/latex] tako da vrijedi [latex]|a_{n} - a|<{\varepsilon}[/latex], to jest nakon nekog člana niza, svi su strpani u interval [latex]\left\langle a-\varepsilon,a+\varepsilon\right\rangle[/latex]. Kako je [latex]a[/latex] limes, tada koliko god ti suzio interval oko njega, uvijek će u tom intervalu biti beskonačno mnogo članova niza, to jest postojati će prirodan [latex]n_1[/latex] takav da su nakon člana [latex]a_{n_1}[/latex] niza [latex](a_n)[/latex] svi preostali članovi strpani u interval [latex]\left\langle a-\frac{\varepsilon}{M+|b|},a+\frac{\varepsilon}{M+|b|}\right\rangle [/latex] ili drugačije zapisano [latex]|a_n - a|<\dfrac{\epsilon}{M+|b|}.[/latex]
Iz slijedećega možeš vidjeti zašto je bilo potrebno suziti interval za [latex]\frac{1}{M+|b|}\colon[/latex]
[latex]\displaystyle |a_n b_n -ab|<|a_n||b_n - b |+|b||a_n - a|<|a_n|\frac{\varepsilon}{M + |b|}+|b|\frac{\varepsilon}{M+|b|}=\varepsilon \frac{|a_n|+|b|}{M+|b|}[/latex]
a to je manje od [latex]\varepsilon[/latex] jer je [latex]\frac{|a_n|+|b|}{M+|b|}<1[/latex].
Zbog naštimavanja za provjeravanje konvergencije od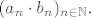 
Niz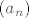 
(analogno za niz 
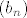) je konvergentan pa za svaki pozitivan 
postoji 
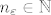tako da vrijedi 
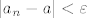, to jest nakon nekog člana niza, svi su strpani u interval 
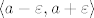. Kako je 
limes, tada koliko god ti suzio interval oko njega, uvijek će u tom intervalu biti beskonačno mnogo članova niza, to jest postojati će prirodan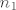 
takav da su nakon člana 
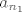niza 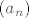svi preostali članovi strpani u interval 
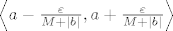ili drugačije zapisano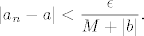 
Iz slijedećega možeš vidjeti zašto je bilo potrebno suziti interval za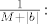 
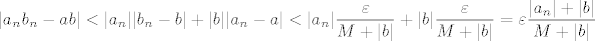
a to je manje od jer je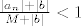 
.
_________________
The Dude Abides
