| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 0:44 ned, 24. 2. 2008 Naslov: Postano: 0:44 ned, 24. 2. 2008 Naslov: |
    |
|
|
a koji dio ti točno nije jasan? :?
pretpostavljam da te muči ovaj dio oko odabira podnizova.
zaključili smo (zbog ekvivalencije normi na R^n) da svi koordinatni nizovi konvergiraju. e sad, mi smo ovdje (jer je tako jednostavno prirodno :) ) krenuli od prvog koordinatnog niza. on je ograničen, pa nam b-w u R kaže da ima konvergentan podniz [latex](a^{p_1(k)}_1)_{k \in \mathbb{N}}[/latex]. kako je i drugi koordinatni niz [latex](a^k_2)_{k \in \mathbb{N}}[/latex] ograničen, i svaki njegov podniz je ograničen. sad uzmemo baš one indekse iz podniza prvog koordinatnog niza, a sve u cilju toga da na kraju za svaki koordinatni podniz imamo iste indekse. :wink:
dakle, [latex](a^{p_1(k)}_2)_{k \in \mathbb{N}}[/latex] je ograničen, pa postoji njegov koordinatni podniz. označimo ga s [latex](a^{p_2(k)}_1)_{k \in \mathbb{N}}[/latex]. to radimo do zadnjeg koordinatnog niza.
na kraju: [latex]p_n(k)[/latex] je podniz od [latex]p_{n-1}(k)[/latex], koji je podniz od [latex]p_{n-2}(k)[/latex], koji je podniz od [latex]p_{n-3}(k)[/latex], ... , koji je podniz od [latex]p_1(k)[/latex].
[latex]p_n(k)[/latex] je, dakle, podniz svih do sada. zato njega uzmemo kao konačnog. možemo zaključiti da je limes početnog niza vektor čije su komponente limesi koordinatnih nizova. :D
ja se sada bojim da je sve nejasnije. meni je. :x
a koji dio ti točno nije jasan? 
pretpostavljam da te muči ovaj dio oko odabira podnizova.
zaključili smo (zbog ekvivalencije normi na R^n) da svi koordinatni nizovi konvergiraju. e sad, mi smo ovdje (jer je tako jednostavno prirodno  ) krenuli od prvog koordinatnog niza. on je ograničen, pa nam b-w u R kaže da ima konvergentan podniz ) krenuli od prvog koordinatnog niza. on je ograničen, pa nam b-w u R kaže da ima konvergentan podniz 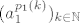 . kako je i drugi koordinatni niz . kako je i drugi koordinatni niz 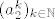 ograničen, i svaki njegov podniz je ograničen. sad uzmemo baš one indekse iz podniza prvog koordinatnog niza, a sve u cilju toga da na kraju za svaki koordinatni podniz imamo iste indekse. ograničen, i svaki njegov podniz je ograničen. sad uzmemo baš one indekse iz podniza prvog koordinatnog niza, a sve u cilju toga da na kraju za svaki koordinatni podniz imamo iste indekse. 
dakle, 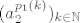 je ograničen, pa postoji njegov koordinatni podniz. označimo ga s je ograničen, pa postoji njegov koordinatni podniz. označimo ga s 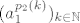 . to radimo do zadnjeg koordinatnog niza. . to radimo do zadnjeg koordinatnog niza.
na kraju: 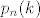 je podniz od je podniz od 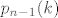 , koji je podniz od , koji je podniz od 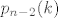 , koji je podniz od , koji je podniz od 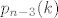 , ... , koji je podniz od , ... , koji je podniz od 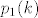 . .
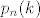 je, dakle, podniz svih do sada. zato njega uzmemo kao konačnog. možemo zaključiti da je limes početnog niza vektor čije su komponente limesi koordinatnih nizova. je, dakle, podniz svih do sada. zato njega uzmemo kao konačnog. možemo zaključiti da je limes početnog niza vektor čije su komponente limesi koordinatnih nizova. 
ja se sada bojim da je sve nejasnije. meni je. 
_________________
ima let u finish
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
 Postano: 21:51 ned, 24. 2. 2008 Naslov: Postano: 21:51 ned, 24. 2. 2008 Naslov: |
    |
|
|
[quote="ivanzub"]hvala puno.
evo imam jos jedno pitanje:
6. zad iz zavrsnog- ako je f neprekinda i K kompaktan:
a) koj je primjer da je i f(K) komp?
[/quote]
f : [0,1] -> IR, f(x) = c.
f([0,1]) = {c}
[quote]
b) je li f^-1 (K) komp. i koji je primjer za to? taj dokaz nismo radili ili..?
ne mogu ga nigdje naci u skripti
[/quote]
Nije. Kontraprimjer:
f : IR -> IR, f(x) = c
f^-1({c}) = IR, IR nije kompaktan jer nije omedjen.
| ivanzub (napisa): | hvala puno.
evo imam jos jedno pitanje:
6. zad iz zavrsnog- ako je f neprekinda i K kompaktan:
a) koj je primjer da je i f(K) komp?
|
f : [0,1] → IR, f(x) = c.
f([0,1]) = {c}
| Citat: |
b) je li f^-1 (K) komp. i koji je primjer za to? taj dokaz nismo radili ili..?
ne mogu ga nigdje naci u skripti
|
Nije. Kontraprimjer:
f : IR → IR, f(x) = c
f^-1({c}) = IR, IR nije kompaktan jer nije omedjen.
_________________
...He never had looked less like captain of any-thing, even his own soul.
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
 Postano: 23:32 ned, 24. 2. 2008 Naslov: Postano: 23:32 ned, 24. 2. 2008 Naslov: |
    |
|
|
[quote="ivanzub"]
6. zad iz zavrsnog- ako je f neprekinda i K kompaktan:
a) koj je primjer da je i f(K) komp?[/quote]
Kaj nije neprekidna slika kompakta uvijek kompakt?
Ako bas zelis vidjeti primjer kojeg mozes nacrtati,
za fju vise varijabli: uzmi identitetu s R^2 u R^2. Ona prebacuje bilo koji kompaktan skup u kompaktan skup.
Ili uzmi neku linearnu funkciju s R^2 u R^2. Na primjer, f(x,y)=(x+1,2y). Onda nacrtaj neki kompaktni skup, na primjer kvadratic s vrhovima (0,0), (0,1), (1,0), (1,1), i vidi gdje ga ta funkcija prebaci (mozes crtati ili napisati 2-3 nejednakosti).
[quote="ivanzub"]
b) je li f^-1 (K) komp. i koji je primjer za to? taj dokaz nismo radili ili..?
ne mogu ga nigdje naci u skripti [/quote]
f^-1(K) nije uvijek kompaktna (to znaci opcenito nije, al se moze deisit da je). Npr, ako ti je funkcija identiteta, onda ce f^-1(K) uvijek biti kompaktan (jer je naprosto jednak K). Inace moras racunati primjer po primjer.
f^-1(Y), za bilo koji skup Y, racunas tako da gledas koje sve tocke iz domene se preskikaju u Y u kodomenu. Napises jednadzbu f(x)\in Y, i pokusavas naci koje uvjete x\in X mora zadovoljavati.
| ivanzub (napisa): |
6. zad iz zavrsnog- ako je f neprekinda i K kompaktan:
a) koj je primjer da je i f(K) komp? |
Kaj nije neprekidna slika kompakta uvijek kompakt?
Ako bas zelis vidjeti primjer kojeg mozes nacrtati,
za fju vise varijabli: uzmi identitetu s R^2 u R^2. Ona prebacuje bilo koji kompaktan skup u kompaktan skup.
Ili uzmi neku linearnu funkciju s R^2 u R^2. Na primjer, f(x,y)=(x+1,2y). Onda nacrtaj neki kompaktni skup, na primjer kvadratic s vrhovima (0,0), (0,1), (1,0), (1,1), i vidi gdje ga ta funkcija prebaci (mozes crtati ili napisati 2-3 nejednakosti).
| ivanzub (napisa): |
b) je li f^-1 (K) komp. i koji je primjer za to? taj dokaz nismo radili ili..?
ne mogu ga nigdje naci u skripti |
f^-1(K) nije uvijek kompaktna (to znaci opcenito nije, al se moze deisit da je). Npr, ako ti je funkcija identiteta, onda ce f^-1(K) uvijek biti kompaktan (jer je naprosto jednak K). Inace moras racunati primjer po primjer.
f^-1(Y), za bilo koji skup Y, racunas tako da gledas koje sve tocke iz domene se preskikaju u Y u kodomenu. Napises jednadzbu f(x)\in Y, i pokusavas naci koje uvjete x\in X mora zadovoljavati.
_________________
A comathematician is a device for turning cotheorems into ffee. A cotheorem is, naturally, an easy nsequence of a rollary.
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|









