| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
andy32
Forumaš(ica)

Pridružen/a: 24. 04. 2008. (14:35:24)
Postovi: (4)16
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
andy32
Forumaš(ica)

Pridružen/a: 24. 04. 2008. (14:35:24)
Postovi: (4)16
|
|
| [Vrh] |
|
andy32
Forumaš(ica)

Pridružen/a: 24. 04. 2008. (14:35:24)
Postovi: (4)16
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
 Postano: 17:09 čet, 24. 4. 2008 Naslov: Postano: 17:09 čet, 24. 4. 2008 Naslov: |
    |
|
|
[quote="andy32"]imam jos jedno pitanje, primjer 2.10, kako odmah na pocetku iz ove kongruencije s kvadratnom jednadžbom dobije ova dva rjesenja, u objasnjenju je to preskoceno...[/quote]
ako sam dobro shvatila što te muči, uvrštavaj brojeve 0, 1, 2, ..., 6 u x2 + x + 47 ≡ 0 (mod 7) pa vidiš koja ti pašu (znaš da treba imati 2 rješenja jer je to drugog stupnja)
pa su rješenja 1 i 5
| andy32 (napisa): | | imam jos jedno pitanje, primjer 2.10, kako odmah na pocetku iz ove kongruencije s kvadratnom jednadžbom dobije ova dva rjesenja, u objasnjenju je to preskoceno... |
ako sam dobro shvatila što te muči, uvrštavaj brojeve 0, 1, 2, ..., 6 u x2 + x + 47 ≡ 0 (mod 7) pa vidiš koja ti pašu (znaš da treba imati 2 rješenja jer je to drugog stupnja)
pa su rješenja 1 i 5
_________________
I aim to misbehave
|
|
| [Vrh] |
|
andy32
Forumaš(ica)

Pridružen/a: 24. 04. 2008. (14:35:24)
Postovi: (4)16
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pina
Gost
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
 Postano: 19:13 čet, 24. 4. 2008 Naslov: Postano: 19:13 čet, 24. 4. 2008 Naslov: |
    |
|
|
[quote="tihana"]
"(2/p)=1 za p=1, 7 (mod8)
[/quote]
To je po Teoremu 3.5 iz skripte.
[quote="tihana"]
(3/p)=-1 za p=5, 7 (mod12)
[/quote]
Gledamo dva slucaja: p==1 (mod 4) i p==3 (mod 4).
1) ako je p==1 (mod 4), onda je (3/p)=(p/3)=-1, pa je p kvadratni neostatak modulo 3, sto znaci da je p==2 (mod 3). Iz sustava p==1 (mod 4), p==2 (mod 3) dobivamo (po Kineskom teoremu o ostacima ili uvrstavanjem brojeva od 0 do 11) da je p==5 (mod 12).
2) ako je p==3 (mod 4), onda je (3/p)=-(p/3), tj. (p/3)=1,
pa je p==1 (mod 3). Iz sustava p==3 (mod 4), p==1 (mod 3) dobivamo p==7 (mod 12).
| tihana (napisa): |
"(2/p)=1 za p=1, 7 (mod8)
|
To je po Teoremu 3.5 iz skripte.
| tihana (napisa): |
(3/p)=-1 za p=5, 7 (mod12)
|
Gledamo dva slucaja: p==1 (mod 4) i p==3 (mod 4).
1) ako je p==1 (mod 4), onda je (3/p)=(p/3)=-1, pa je p kvadratni neostatak modulo 3, sto znaci da je p==2 (mod 3). Iz sustava p==1 (mod 4), p==2 (mod 3) dobivamo (po Kineskom teoremu o ostacima ili uvrstavanjem brojeva od 0 do 11) da je p==5 (mod 12).
2) ako je p==3 (mod 4), onda je (3/p)=-(p/3), tj. (p/3)=1,
pa je p==1 (mod 3). Iz sustava p==3 (mod 4), p==1 (mod 3) dobivamo p==7 (mod 12).
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
 Postano: 19:17 čet, 24. 4. 2008 Naslov: Postano: 19:17 čet, 24. 4. 2008 Naslov: |
    |
|
|
[quote="pina"]a mene zanima kako smo u primjeru 2.2 iz skripte, iz ovoga 6x2≡3(mod 7) dobili x2=4 jer ja fakat ne kuzim
pa ako ima koja dobra dusa da me razveseli[/quote]
Uvrstiti redom x2=0,1,2,3,4,5,6 dok se ne nadje rjesenje,
ili rjesavati kao sto smo rekli da se rjesava linearna kongruencija ax==b (mod m) (Euklidov algoritam, ... - vidjeti Primjer 2.1 u skripti).
| pina (napisa): | a mene zanima kako smo u primjeru 2.2 iz skripte, iz ovoga 6x2≡3(mod 7) dobili x2=4 jer ja fakat ne kuzim
pa ako ima koja dobra dusa da me razveseli |
Uvrstiti redom x2=0,1,2,3,4,5,6 dok se ne nadje rjesenje,
ili rjesavati kao sto smo rekli da se rjesava linearna kongruencija ax==b (mod m) (Euklidov algoritam, ... - vidjeti Primjer 2.1 u skripti).
|
|
| [Vrh] |
|
Sasuke
Forumaš(ica)

Pridružen/a: 27. 06. 2005. (19:22:00)
Postovi: (47)16
Spol: 
Lokacija: zemlja
|
|
| [Vrh] |
|
lunjo
Forumaš(ica)


Pridružen/a: 08. 07. 2006. (19:41:05)
Postovi: (1D)16
Spol: 
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
 Postano: 1:10 pet, 25. 4. 2008 Naslov: Postano: 1:10 pet, 25. 4. 2008 Naslov: |
    |
|
|
Algoritam:
trazimo najmanji primitivni korijen modulo n (za sve ostale, postupak se provede do kraja) za npr n prost, znamo da ih ima tocno [latex]\varphi(p-1)[/latex]
uzmemo [latex]\varphi(n)[/latex] (izracunamo, ili ocitamo od nekamo, votevr :) )
rastavimo ga na proste faktore, znaci imamo
[latex]\varphi(n) = p_1^{\alpha_1} \cdot p_2^{\alpha_2} \cdots p_r^{\alpha_r} [/latex]
definiramo si pomocnu oznaku
[latex]k_i = \frac{\varphi(n)}{p_i}), \foreach i \in \{i, \ldots, r\}[/latex]
sad provjeravamo da li je neki broj prim. korijen
trazimo najmanji, pa krenemo redom od najmanjeg prema najvecem
dakle, uzimamo a redom [latex]a = 2, 3, 4, \ldots[/latex] sa dodatnim svojstvom [latex](a,n)=1[/latex] tj. rel prosti sa modulom
i provjeravamo, ZA SVAKI [b]i[/b] :!:
da li cemo dobiti [latex]a^{k_i} \not \equiv 1 \pmod {n}[/latex]
ukoliko za neki a to vrijedi, znaci da izraz 'padne' za svaki eksponent, taj je primitivni korijen
tj. ukoliko nam vrijedi kongruencija, taj a nije p.k. :) i idemo gledati za iduci a
Algoritam:
trazimo najmanji primitivni korijen modulo n (za sve ostale, postupak se provede do kraja) za npr n prost, znamo da ih ima tocno 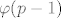
uzmemo 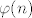 (izracunamo, ili ocitamo od nekamo, votevr (izracunamo, ili ocitamo od nekamo, votevr  ) )
rastavimo ga na proste faktore, znaci imamo
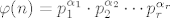
definiramo si pomocnu oznaku
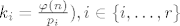
sad provjeravamo da li je neki broj prim. korijen
trazimo najmanji, pa krenemo redom od najmanjeg prema najvecem
dakle, uzimamo a redom 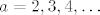 sa dodatnim svojstvom sa dodatnim svojstvom 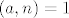 tj. rel prosti sa modulom tj. rel prosti sa modulom
i provjeravamo, ZA SVAKI i 
da li cemo dobiti 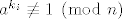
ukoliko za neki a to vrijedi, znaci da izraz 'padne' za svaki eksponent, taj je primitivni korijen
tj. ukoliko nam vrijedi kongruencija, taj a nije p.k.  i idemo gledati za iduci a i idemo gledati za iduci a
|
|
| [Vrh] |
|
|













