| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
predrag
Gost
|
 Postano: 12:15 uto, 1. 4. 2008 Naslov: Molim provjeru računalom Postano: 12:15 uto, 1. 4. 2008 Naslov: Molim provjeru računalom |
    |
|
|
Pozdrav,
Imam jedan problem koji zahtjeva provjeru računalom.
Imam sustav:
2x1 + 3x2 + x5 + x6 = 84
x6 + x8 + x9 +x12 = 45
x1 + x8 + x14 +x19 =46
x1 + x10 + x11 + x13 +2x14 =58
x1 + x3 + x4 + x8 + x14 =52
x6 + 2x7 + 2x8 + 3x10 + x16=130
x1+ x2 + x13 + 3x14 + x18 = 71
x5 + 2x12 + x13 + x16 + x18 = 70
x7 +x8 + x12 + x13 + x15 + x18 =104
x1 + x4 + x5 +2x12 + x13 + x14 + 2x15 +x17=129
x3 + x10 + x12 + 2x13 + x15 =51¸
x1 + x6 + x8 +x12 + x14 + x18 =92
x5 + x8 +x10 + x11 + x12 + x14 =58
x4 + x5 + x7 + 3x13 + x15 + x17 +x18 =108
x12 + x13 + x14 + 2x16 + x17 =80
Ovo je sustav 15 linearnih jednadžbi sa 19 nepoznanica.
UVIJET na sustav je da su sve nepoznanice prirodni brojevi ,uključujući i 0,iz skupa {0,1,2,...,52}.Znam jedno rješenje ,ali to mi ništa ne pomaže da pronađem druga (ako ona postoje).Prvotna ideja mi je bila da se promatra peta jednadžba sa 5 nepoznanica i biraju sve moguće vrijednosti iz skupa {0,1,2,...,52} ,a onda da računalo ispita metodom Gaussove eliminacije sustave 14 jednadžbi sa 14 nepoznanica.Metodom "grube sile" to se može napraviti da se prolazi kroz 5 petlji ,a onda poziva neka procedura Gauss.Npr
_________________
FOR I:= 0 TO 52 DO
FOR J:= 0 T0 52 DO
.
.
FOR M:=0 TO 52 DO
Gauss
_________________
No "problemčić" je da je to ukupno 53^5= 418 195 493 sustava.
Ne znam koliko dugo moj PC treba za provjeru jednog sustava ovog tipa ,ali imam velike probleme sa ovakvim pristupom.
Drugi pristup je pametniji,ali kako nisam programer (nemam čak ni programski paket kao Mathematica) ne znam ga implementirati.
Naime peta jednadzba x1 + x3 + x4 + x8 + x14 =52
Nema 418 miliona rješenja nego samo
54!/(4!50!) = 316 251 rješenja pod danim uvijetom
Pliz,ako mi neka dobra duša vična korištenju gotovih softverskih paketa i/ili programiranu može ovo riješiti.Ovo mi jako važno.
Ne trebam programski kod kao riješenje ovog zadatka nego samo provjeru i odgovor na pitanje: [b]Ima li problem samo jedno rješenje
ili ako nema koliko ih ima ?[/b]
Predrag
Pozdrav,
Imam jedan problem koji zahtjeva provjeru računalom.
Imam sustav:
2x1 + 3x2 + x5 + x6 = 84
x6 + x8 + x9 +x12 = 45
x1 + x8 + x14 +x19 =46
x1 + x10 + x11 + x13 +2x14 =58
x1 + x3 + x4 + x8 + x14 =52
x6 + 2x7 + 2x8 + 3x10 + x16=130
x1+ x2 + x13 + 3x14 + x18 = 71
x5 + 2x12 + x13 + x16 + x18 = 70
x7 +x8 + x12 + x13 + x15 + x18 =104
x1 + x4 + x5 +2x12 + x13 + x14 + 2x15 +x17=129
x3 + x10 + x12 + 2x13 + x15 =51¸
x1 + x6 + x8 +x12 + x14 + x18 =92
x5 + x8 +x10 + x11 + x12 + x14 =58
x4 + x5 + x7 + 3x13 + x15 + x17 +x18 =108
x12 + x13 + x14 + 2x16 + x17 =80
Ovo je sustav 15 linearnih jednadžbi sa 19 nepoznanica.
UVIJET na sustav je da su sve nepoznanice prirodni brojevi ,uključujući i 0,iz skupa {0,1,2,...,52}.Znam jedno rješenje ,ali to mi ništa ne pomaže da pronađem druga (ako ona postoje).Prvotna ideja mi je bila da se promatra peta jednadžba sa 5 nepoznanica i biraju sve moguće vrijednosti iz skupa {0,1,2,...,52} ,a onda da računalo ispita metodom Gaussove eliminacije sustave 14 jednadžbi sa 14 nepoznanica.Metodom "grube sile" to se može napraviti da se prolazi kroz 5 petlji ,a onda poziva neka procedura Gauss.Npr
_________________
FOR I:= 0 TO 52 DO
FOR J:= 0 T0 52 DO
.
.
FOR M:=0 TO 52 DO
Gauss
_________________
No "problemčić" je da je to ukupno 53^5= 418 195 493 sustava.
Ne znam koliko dugo moj PC treba za provjeru jednog sustava ovog tipa ,ali imam velike probleme sa ovakvim pristupom.
Drugi pristup je pametniji,ali kako nisam programer (nemam čak ni programski paket kao Mathematica) ne znam ga implementirati.
Naime peta jednadzba x1 + x3 + x4 + x8 + x14 =52
Nema 418 miliona rješenja nego samo
54!/(4!50!) = 316 251 rješenja pod danim uvijetom
Pliz,ako mi neka dobra duša vična korištenju gotovih softverskih paketa i/ili programiranu može ovo riješiti.Ovo mi jako važno.
Ne trebam programski kod kao riješenje ovog zadatka nego samo provjeru i odgovor na pitanje: Ima li problem samo jedno rješenje
ili ako nema koliko ih ima ?
Predrag
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 13:09 uto, 1. 4. 2008 Naslov: Postano: 13:09 uto, 1. 4. 2008 Naslov: |
    |
|
|
Ovako, na brzinu, Mathematica daje slijedece:
[code:1]sol = Solve[
{
2x1 + 3x2 + x5 + x6 == 84,
x6 + x8 + x9 + x12 == 45,
x1 + x8 + x14 + x19 == 46,
x1 + x10 + x11 + x13 + 2x14 == 58,
x1 + x3 + x4 + x8 + x14 == 52,
x6 + 2x7 + 2x8 + 3x10 + x16 == 130,
x1 + x2 + x13 + 3x14 + x18 == 71,
x5 + 2x12 + x13 + x16 + x18 == 70,
x7 + x8 + x12 + x13 + x15 + x18 == 104,
x1 + x4 + x5 + 2x12 + x13 + x14 + 2x15 + x17 == 129,
x3 + x10 + x12 + 2x13 + x15 == 51,
x1 + x6 + x8 + x12 + x14 + x18 == 92,
x5 + x8 + x10 + x11 + x12 + x14 == 58,
x4 + x5 + x7 + 3x13 + x15 + x17 + x18 == 108,
x12 + x13 + x14 + 2x16 + x17 == 80
},
{x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12, x13, x14, x15}
]
{
{
x1 -> 1/471 ((876 + 326 x16 + 333 x17 - 156 x18 - 207 x19)),
x2 -> 1/157 ((7617 - 343 x16 - 216 x17 + 220 x18 - 10 x19)),
x3 -> 1/471 (((-39102) + 1957 x16 + 1437 x17 - 1263 x18 + 507 x19)),
x4 -> 1/471 ((41928 - 1957 x16 - 1437 x17 + 1263 x18 - 36 x19)),
x5 -> 1/157 (((-9977) + 558 x16 + 334 x17 - 346 x18 + 30 x19)),
x6 -> 1/471 (((-810) + 761 x16 + 276 x17 - 630 x18 + 414 x19)),
x7 -> 1/471 (((-8841) + 1322 x16 + 1125 x17 - 1329 x18 + 510 x19)),
x8 -> 1/157 ((7845 - 256 x16 - 196 x17 + 188 x18 - 137 x19)),
x9 -> 1/157 (((-8002) + 256 x16 + 196 x17 - 31 x18 - 20 x19)),
x10 -> (-(2/157)) (((-1814) + 130 x16 + 75 x17 - 120 x18 + 34 x19)),
x11 -> 1/471 ((3099 + 193 x16 + 57 x17 + 3 x18 + 321 x19)),
x12 -> 1/471 ((22476 - 761 x16 - 276 x17 + 159 x18 + 57 x19)),
x13 -> 1/471 ((17949 - 623 x16 - 450 x17 + 249 x18 - 204 x19)),
x14 -> 1/471 (((-2745) + 442 x16 + 255 x17 - 408 x18 + 147 x19)),
x15 -> 1/471 (((-6135) + 830 x16 + 189 x17 - 114 x18 + 48 x19))
}
}[/code:1]
Sada bi se trebalo dati zavrtiti cetiri petlje (za varijable [tt]x16[/tt], [tt]x17[/tt], [tt]x18[/tt] i [tt]x19[/tt], vrijednosti od 0 do 52), sto je [latex]53^4 = 7890481[/latex] racunanja gornjih varijabli i provjeravanja jesu li cjelobrojne (ovo treba raditi u cjelobrojnoj aritmetici!). :)
Kod koji bi to trebao raditi u Mathematici bi bio (sorry na nespretnosti; nisam doma s Mathematicom):
[code:1]s[a16_, a17_, a18_, a19_] := sol /. {x16 -> a16, x17 -> a17, x18 -> a18, x19 -> a19}
For[a = 0, a <= 52, a++,
For[b = 0, b <= 52, b++,
For[c = 0, c <= 52, c++,
For[d = 0, d <= 52, d++,
x = s[a, b, c, d][[1]];
ok = True;
For[e = 1, e <= Length[x], e++,
If[Not[IntegerQ[x[[e]][[2]]]], ok = False; Break[]]
];
If[ok, Print[{s, x}]]
]
]
]
][/code:1]
Na zalost, meni za prvih 10 [tt]b[/tt]-ova treba pola minute, sto znaci cca 3 sekunde po jednome, a to je ukupno [latex]52^2\cdot3=8112[/latex] sekundi, tj. oko 2 sata i 15 minuta (uz pretpostavku da nisam fulao u samom kodu). :?
Iskodirano u necem brzem (npr. u C-u) bi trebalo biti znatno brze, no to mozes i sam. ;)
Ovako, na brzinu, Mathematica daje slijedece:
| Kod: | sol = Solve[
{
2x1 + 3x2 + x5 + x6 == 84,
x6 + x8 + x9 + x12 == 45,
x1 + x8 + x14 + x19 == 46,
x1 + x10 + x11 + x13 + 2x14 == 58,
x1 + x3 + x4 + x8 + x14 == 52,
x6 + 2x7 + 2x8 + 3x10 + x16 == 130,
x1 + x2 + x13 + 3x14 + x18 == 71,
x5 + 2x12 + x13 + x16 + x18 == 70,
x7 + x8 + x12 + x13 + x15 + x18 == 104,
x1 + x4 + x5 + 2x12 + x13 + x14 + 2x15 + x17 == 129,
x3 + x10 + x12 + 2x13 + x15 == 51,
x1 + x6 + x8 + x12 + x14 + x18 == 92,
x5 + x8 + x10 + x11 + x12 + x14 == 58,
x4 + x5 + x7 + 3x13 + x15 + x17 + x18 == 108,
x12 + x13 + x14 + 2x16 + x17 == 80
},
{x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12, x13, x14, x15}
]
{
{
x1 -> 1/471 ((876 + 326 x16 + 333 x17 - 156 x18 - 207 x19)),
x2 -> 1/157 ((7617 - 343 x16 - 216 x17 + 220 x18 - 10 x19)),
x3 -> 1/471 (((-39102) + 1957 x16 + 1437 x17 - 1263 x18 + 507 x19)),
x4 -> 1/471 ((41928 - 1957 x16 - 1437 x17 + 1263 x18 - 36 x19)),
x5 -> 1/157 (((-9977) + 558 x16 + 334 x17 - 346 x18 + 30 x19)),
x6 -> 1/471 (((-810) + 761 x16 + 276 x17 - 630 x18 + 414 x19)),
x7 -> 1/471 (((-8841) + 1322 x16 + 1125 x17 - 1329 x18 + 510 x19)),
x8 -> 1/157 ((7845 - 256 x16 - 196 x17 + 188 x18 - 137 x19)),
x9 -> 1/157 (((-8002) + 256 x16 + 196 x17 - 31 x18 - 20 x19)),
x10 -> (-(2/157)) (((-1814) + 130 x16 + 75 x17 - 120 x18 + 34 x19)),
x11 -> 1/471 ((3099 + 193 x16 + 57 x17 + 3 x18 + 321 x19)),
x12 -> 1/471 ((22476 - 761 x16 - 276 x17 + 159 x18 + 57 x19)),
x13 -> 1/471 ((17949 - 623 x16 - 450 x17 + 249 x18 - 204 x19)),
x14 -> 1/471 (((-2745) + 442 x16 + 255 x17 - 408 x18 + 147 x19)),
x15 -> 1/471 (((-6135) + 830 x16 + 189 x17 - 114 x18 + 48 x19))
}
} |
Sada bi se trebalo dati zavrtiti cetiri petlje (za varijable x16, x17, x18 i x19, vrijednosti od 0 do 52), sto je 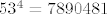 racunanja gornjih varijabli i provjeravanja jesu li cjelobrojne (ovo treba raditi u cjelobrojnoj aritmetici!). racunanja gornjih varijabli i provjeravanja jesu li cjelobrojne (ovo treba raditi u cjelobrojnoj aritmetici!). 
Kod koji bi to trebao raditi u Mathematici bi bio (sorry na nespretnosti; nisam doma s Mathematicom):
| Kod: | s[a16_, a17_, a18_, a19_] := sol /. {x16 -> a16, x17 -> a17, x18 -> a18, x19 -> a19}
For[a = 0, a <= 52, a++,
For[b = 0, b <= 52, b++,
For[c = 0, c <= 52, c++,
For[d = 0, d <= 52, d++,
x = s[a, b, c, d][[1]];
ok = True;
For[e = 1, e <= Length[x], e++,
If[Not[IntegerQ[x[[e]][[2]]]], ok = False; Break[]]
];
If[ok, Print[{s, x}]]
]
]
]
] |
Na zalost, meni za prvih 10 b-ova treba pola minute, sto znaci cca 3 sekunde po jednome, a to je ukupno 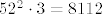 sekundi, tj. oko 2 sata i 15 minuta (uz pretpostavku da nisam fulao u samom kodu). sekundi, tj. oko 2 sata i 15 minuta (uz pretpostavku da nisam fulao u samom kodu). 
Iskodirano u necem brzem (npr. u C-u) bi trebalo biti znatno brze, no to mozes i sam. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 14:14 uto, 1. 4. 2008 Naslov: Postano: 14:14 uto, 1. 4. 2008 Naslov: |
    |
|
|
Meni su 4 for petlje sa vulgaris kodom izbacile 10 rješenja za manje od pola minute. Funkcijom [tt]IntegerQ[][/tt] sam provjeravao da li su x1,...,x15 cijeli i još dodao da za svaki x_i mora vrijediti 0<=x_i<=52. Ako je sve zadovoljeno, tada ispisuje četvorku (x16,x17,x18,x19).
Rješenja bi trebala biti (15,26,20,0), (18,24,22,0), (21,18,22,11), (24,17,26,2), (24,22,31,4), (27,11,26,13), (27,15,28,2), (30,13,30,2), (33,6,27,0),(36,0,27,11).
Meni su 4 for petlje sa vulgaris kodom izbacile 10 rješenja za manje od pola minute. Funkcijom IntegerQ[] sam provjeravao da li su x1,...,x15 cijeli i još dodao da za svaki x_i mora vrijediti 0⇐x_i⇐52. Ako je sve zadovoljeno, tada ispisuje četvorku (x16,x17,x18,x19).
Rješenja bi trebala biti (15,26,20,0), (18,24,22,0), (21,18,22,11), (24,17,26,2), (24,22,31,4), (27,11,26,13), (27,15,28,2), (30,13,30,2), (33,6,27,0),(36,0,27,11).
_________________
The Dude Abides
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
predrag
Forumaš(ica)

Pridružen/a: 02. 04. 2008. (15:35:11)
Postovi: (4)16
Lokacija: Zagreb
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 17:24 sri, 2. 4. 2008 Naslov: Postano: 17:24 sri, 2. 4. 2008 Naslov: |
    |
|
|
Koristenjem Goranovog rjesenja prvog sustava:
[code:1]sol = Solve[{2x1 + 3x2 + x5 + x6 == 84, x6 + x8 + x9 + x12 == 45,
x1 + x8 + x14 + x19 == 46, x1 + x10 + x11 + x13 + 2x14 == 58,
x1 + x3 + x4 + x8 + x14 == 52, x6 + 2x7 + 2x8 + 3x10 + x16 == 130,
x1 + x2 + x13 + 3x14 + x18 == 71, x5 + 2x12 + x13 + x16 + x18 == 70,
x7 + x8 + x12 + x13 + x15 + x18 == 104,
x1 + x4 + x5 + 2x12 + x13 + x14 + 2x15 + x17 == 129,
x3 + x10 + x12 + 2x13 + x15 == 51,
x1 + x6 + x8 + x12 + x14 + x18 == 92,
x5 + x8 + x10 + x11 + x12 + x14 == 58,
x4 + x5 + x7 + 3x13 + x15 + x17 + x18 == 108,
x12 + x13 + x14 + 2x16 + x17 == 80}, {x1, x2, x3, x4, x5, x6, x7, x8,
x9, x10, x11, x12, x13, x14, x15}];
solutions = {{21, 18, 22, 11}, {24, 17, 26, 2}, {24, 22, 31, 4}, {27, 11, 26,
13}, {27, 15, 28, 2}};
s[x_] := sol /. {x16 -> x[[1]], x17 -> x[[2]], x18 -> x[[3]], x19 -> x[[4]]};
For[i = 1, i <= Length[solutions], i++, x = s[solutions[[i]]][[1]];
ok = True;
For[e = 1, e <= Length[x], e++,
xx = x[[e]][[2]];
If[Or[
Not[IntegerQ[xx]],
xx < 1,
xx > 52
],
ok = False; Break[]
]
];
If[ok, Print[{solutions[[i]], x}]]
][/code:1]
dobijem dva rjesenja koja zadovoljavaju uvjet da su svi [i]x[/i]-evi cijeli brojevi strogo veci od 0 i strogo manji od 53:
[code:1]{{24, 17, 26, 2}, {x1 -> 21, x2 -> 9, x3 -> 1, x4 -> 7, x5 -> 1, x6 -> 14,
x7 -> 18, x8 -> 19, x9 -> 4, x10 -> 6, x11 -> 20, x12 -> 8, x13 -> 3,
x14 -> 4, x15 -> 30}}
{{27, 15, 28, 2}, {x1 -> 21, x2 -> 8, x3 -> 2, x4 -> 6, x5 -> 3, x6 -> 15,
x7 -> 16, x8 -> 19, x9 -> 6, x10 -> 6, x11 -> 21, x12 -> 5, x13 -> 2,
x14 -> 4, x15 -> 34}}[/code:1]
Prva cetiri broja su [latex]x_{16}, x_{17}, x_{18}, x_{19}[/latex], a ostatak je jasan. 8)
Koristenjem Goranovog rjesenja prvog sustava:
| Kod: | sol = Solve[{2x1 + 3x2 + x5 + x6 == 84, x6 + x8 + x9 + x12 == 45,
x1 + x8 + x14 + x19 == 46, x1 + x10 + x11 + x13 + 2x14 == 58,
x1 + x3 + x4 + x8 + x14 == 52, x6 + 2x7 + 2x8 + 3x10 + x16 == 130,
x1 + x2 + x13 + 3x14 + x18 == 71, x5 + 2x12 + x13 + x16 + x18 == 70,
x7 + x8 + x12 + x13 + x15 + x18 == 104,
x1 + x4 + x5 + 2x12 + x13 + x14 + 2x15 + x17 == 129,
x3 + x10 + x12 + 2x13 + x15 == 51,
x1 + x6 + x8 + x12 + x14 + x18 == 92,
x5 + x8 + x10 + x11 + x12 + x14 == 58,
x4 + x5 + x7 + 3x13 + x15 + x17 + x18 == 108,
x12 + x13 + x14 + 2x16 + x17 == 80}, {x1, x2, x3, x4, x5, x6, x7, x8,
x9, x10, x11, x12, x13, x14, x15}];
solutions = {{21, 18, 22, 11}, {24, 17, 26, 2}, {24, 22, 31, 4}, {27, 11, 26,
13}, {27, 15, 28, 2}};
s[x_] := sol /. {x16 -> x[[1]], x17 -> x[[2]], x18 -> x[[3]], x19 -> x[[4]]};
For[i = 1, i <= Length[solutions], i++, x = s[solutions[[i]]][[1]];
ok = True;
For[e = 1, e <= Length[x], e++,
xx = x[[e]][[2]];
If[Or[
Not[IntegerQ[xx]],
xx < 1,
xx > 52
],
ok = False; Break[]
]
];
If[ok, Print[{solutions[[i]], x}]]
] |
dobijem dva rjesenja koja zadovoljavaju uvjet da su svi x-evi cijeli brojevi strogo veci od 0 i strogo manji od 53:
| Kod: | {{24, 17, 26, 2}, {x1 -> 21, x2 -> 9, x3 -> 1, x4 -> 7, x5 -> 1, x6 -> 14,
x7 -> 18, x8 -> 19, x9 -> 4, x10 -> 6, x11 -> 20, x12 -> 8, x13 -> 3,
x14 -> 4, x15 -> 30}}
{{27, 15, 28, 2}, {x1 -> 21, x2 -> 8, x3 -> 2, x4 -> 6, x5 -> 3, x6 -> 15,
x7 -> 16, x8 -> 19, x9 -> 6, x10 -> 6, x11 -> 21, x12 -> 5, x13 -> 2,
x14 -> 4, x15 -> 34}} |
Prva cetiri broja su 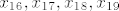 , a ostatak je jasan. , a ostatak je jasan. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
predrag
Forumaš(ica)

Pridružen/a: 02. 04. 2008. (15:35:11)
Postovi: (4)16
Lokacija: Zagreb
|
|
| [Vrh] |
|
|







