Sustav trigonometrijskih jednadžbi (zadatak)

[Zoki114]

Pozdrav. Molio bih za pomoć jednog zadatka za treći razred.
Trebam riješiti ovaj sustav jednadžbi u [0,2Pi]

sin x = cos y
sin y = cos x

Ja sam radio ovako. Prvo sam pomnožio lijeve i desne strane
sin x * sin y = cos y * cos x. Kad se sve prebaci na desnu stranu dobiva se cos(y+x) = 0. To znači y+x = Pi/2 ili y+x = 3Pi/2.
Onda sam pomnožio obrnuto lijevu stranu s desnom i desnu s lijevom pa se dobiva
sin x * cos x = cos y * sin y. Sve na lijevo i dobijemo sin(x-y) = 0 a to je ili x-y = 0 ili x-y = Pi.
Sad kad imamo za svaku jednadžbu po dva slučaja ja sam gledao sve kombinacije pa zapravo ima 4 riješenja

1. y+x = Pi/2 i x-y = 0 daje x = Pi/4, y = Pi/4
2. y+x = Pi/2 i x-y = Pi daje x = 3Pi/4, y = -Pi/4
3. y+x = 3Pi/2 i x-y = 0 daje x = 3Pi/4, y = 3Pi/4
4. y+x = 3Pi/2 i x-y = Pi daje x = 5Pi/4, y = Pi/4

Drugo riješenje izbacujem jer je y manji od 0. I sad bi trebao imati 3 riješenja (makar mi je to čudno ja bi rekao da treba biti 4)ali četvrto riješenje mi uopće ne valja jer je x u trećem kvadrantu a y u prvom. Molim vas gdje sam fulao u riješenju i koliko riješenja taj zadatak uopće ima?? Znam da ima puno načina ali mene muči gdje sam ja tu fulao.

Hvala. Pozdrav

[Gost]

Ovo je pogrešno:

sin x * cos x = cos y * sin y. Sve na lijevo i dobijemo sin(x-y) = 0

[goranm]

Možda je lakše sve zbrojiti.

sinx + siny = cosx + cosy




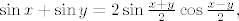
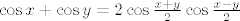
Broj 2 će se pokratiti, a možemo još ubiti jedan kosinus, ali prije toga pogledati da ne dijelimo s nulom:



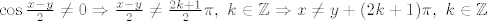
Sada trebamo pogledati da nismo izbacili neka dobra rješenja. Uzmemo npr. sin x = cos y i umjesto x uvrstimo 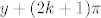. Sada imamo


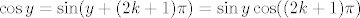
(onaj drugi dio adicione formule je 0 jer je sin((2k+1)pi)=0 za svaki k). Sada može biti cos y = sin y ili cos y = -siny jer 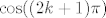će, ovisno o k, biti jednak 1 ili -1. Dalje se lagano provjeri koja su rješenja dobra.

Sada ostaje samo 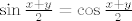, a sin t = cos t za 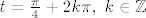i 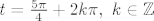. Sada umjesto t uvrstiš (x+y)/2 i dalje bi trebalo biti jasno. Još se treba pogledati da rješenja zadovoljavaju

Sada sam uočio da se radi na [0,2pi] pa se na nekim mjestima umjesto k može pisati 0.

_________________
The Dude Abides