Dodefiniranje funkcije...

[frikmen2]

Evo zadatka, ako netko zna ideju za rješavanje bilo bi korisno...
Dakle,

da li je moguće funkciju dodefinirati tako da bude neprekidna na ?

[Luuka]

L'Hospital mi pada na pamet (imamo 0/0 oblik). treba nam limes ( svi xi-evi teže u nulu) f(x). To treba bit konačan broj, i to proglasimo f(0).
Tu bi trebalo vrijedit da je lim (kad svi teže u 0) = ( lim parc po x1 teži u nulu, ..., lim parc po xn teži u nulu) (zapisano po komponentama). Nek još netko potvrdi ovu slutnju, nazovimo je Luukina slutnja

Pa sad parc deriviramo po xi brojnik i nazivnik i u svakom koraku dobijemo (xi cosxi + sinxi)/(2xi) pa opet deriviramo po xi (ili rastavimo na 2 limesa) i dobijemo 1.
Tako za sve xi pa je odgovor: Da, može se dodefinirati sa f(0)=1.

Molim još potvrdu da se to može tako.

Možda se može i indukcijom po n, al ne vidim neki trik kod raspisivanja u koraku indukcije... ili direktno sređivat pa da se dođe do sinxi/xi oblika, vjerojatno isti trik bi trebao...

EDIT: Luukina slutnja u ovom gore obliku ne vrijedi, jer je naša f sa Rn u R, a ne u Rn, pa ništa od komponentnog zapisa, a i ne bi prošo L'Hospital jer u pojedinoj komponenti ne bi bio 0/0 oblik Al možda postoji nešto slično...

_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy

[ma]

moje rješenje je prilično intuitivno, što u matematici znači da nije dovoljno zadovoljavajuće.
ovako- znači, u nuli imamo problem. e sad, ako se približavamo nuli po svakoj komponenti posebno, tj. sve komponente su nam 0, osim te jedne koja joj je jako blizu (tu ću napisati samo za prvu), vidimo da je pametno dodefinirati f(0)=1.

.

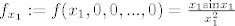
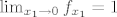tako je za svaki 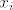, pa se usuđujem reći da smijemo staviti

_________________
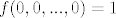
ima let u finish

[goc]

ajmo probat dokazat da dodefiniranje u nuli jednostavno valja
znaci neka je f(0,0,...,0)=1
promatrajmo proizvoljan niz tocaka koje teze u (0,0,...,0),tada je jasno da i duljine tih vektora teze u 0.
funkcija se ne mijenja ako promijenimo predznak bilo koje koordinate pa mozemmo smatrati da su sve pozitivne.
znamo da je sinx<x pa je f(X)=f(x1,x2,...,xn)<1 jer je x1sinx1<x1^2 itd..
ako je tocka (x1,x2,...,xn) proizvoljno blizu nuli(sto znamo da mozemo imati, kasnije cemo tocno vidjeti kolko nam to blizu treba) onda su posebice i njene koordinate proizvoljno blizu nuli.
posto znamo da je limes od sinx/x kad x ide u 0 jednak 1 onda za svaki E>0 postoji D>0 tako da za svaki 0<x<D vrijedi 1-E<sinx/x<1
uzmimo sad proizvoljan E>0 i takav D za koji vrijedi ovo gore.
neka je Xk vektor takav da je za njega i sve vektore poslije njega u tom nizu |x1+|x2|+...+|xn|<D (on postoji)
sad je f(x1,x2,...,xn)=
(x1xinx1+x2sinx2+...+xnsinxn)/(x1^2+x2^2+...+xn^2)>
[x1*x1(1-E)+x2*x2(1-E)+...+xn*xn(1-E)]/(x1^2+x2^2+...+xn^2) =
=1-E
sada je bilo koji niz tocaka koje teze u 0 dokazano da za svaki E>0 postoji neki indeks u nizu tocaka tako da za tu tocku i sve dalje vrijedi
1-E<f(Xk)<1 pa je sad jasno da je limes kad 'k' ide u beskonacno od f(Xi)=1 i funkcija je dobro dodefinirana mrzim se sto sam zaboravio koristiti latex

[Luuka]

Nice goc

Al ja bi tu ipak pitao, jel ima neka verzija L'Hospitala za slične ovakve situacije? Npr ako imamo fju sa Rn->Rn pa tražimo
lim (kad sve koordinate teže nečem) f(x1,...,xn), pa da je to ( lim (x1 teži nekud) f(x1, ?), lim (x2 teži nekud f( ?, x2, ?) ... )= {ako imamo 0/0 ili besk/besk} = sve to sa pripadnim parc derivacijama?

Ak kužite kaj hoću pitat...

_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy