|
za pocetak, jednadzba pravca je u nekom od oblika: (valjda me nazivi dobro sluze :) )
explicitni [latex]y = kx + y_0[/latex]
implicitni [latex]Ax + By + C = 0[/latex]
ono sto ti jos treba, uvijek za znati :) je jednadzba pravca kroz dvije tocke, namely [latex] (x_1, y_1), (x_2, y_2)[/latex]
(edit: ispravljena jdba, pomijesah brojnik i nazivnik :oops: sad je dobro :g:)
[latex] y - y_1 = \frac{y_1 - y_2}{x_1 - x_2}(x - x_1)[/latex]
gdje je ovaj razlomak u stvari koeficijent smjera pravca, znaci onaj k iz prvog oblika :)
y_0 dobijes kad razlomak pomnozis sa x_1 i tome dodas y_1 (no, sredis ovu kobasicu da lijepo pise :) )
takodjer, pravac se moze zadati kao jos pokoje rjesenje sustava jednadzbi
npr, kao presjek dviju ravnina (onda njihovo rjesenje je pravac, ako se ravnine sijeku; je cijela ravnina ako su ravnine jedna te ista, i nema rjesenja ako su ravnine paralelne)
nisi spominjao 3d i ravnine, ali mozda ti zatreba u nekim zadacima kasnije.... :)
anyway, onda u ovoj svojoj teoriji dodajes jos stanje da su 2 pravca mimosmjerna - nemaju zajednickih tocaka i nisu paralelni :)
anyway, ova tvoja teorija bez ovog mog paragrafa je 2D, sa mojim paragrafom je 3D, formule se malo prosire
no, za formule, ako nisi do sada, ajd si odi u knjizaru i kupi tzv 'zute tablice', kartonska zuta harmonika koja ima sve formule srednjoskolske matematike na sebi, i korisna je i pod stare dane :)
cijena bi bila valjda oko 20tak kuna ili tako nesto.... bilo je to davno kad sam to kupovala :)
ajmo sad na tvoje probleme :)
zapravo, ajmo jos jednu konverziju :)
da bi iz implicitnog dobio explicitni (u pravilu cesce baratamo s njime :) ) hitis y da ostane sam i usamljen na svojoj strani, a ostatak sredis kako spada... namely, dobijes
[latex] y = \frac{-Ax - C}{B}[/latex] i to sad lijepo sredis (podijelis sa B sto se dijeliti da - rjesis se razlomaka) - ne zaboraviti UVIJEK paziti na predznake ! :)
ok, sad tvoji problemi
1. sijeku se
znaci, imas ova dva cuda
[latex]y = k_1x + y_1[/latex][latex]y = k_2x + y_2[/latex]
sto znaci rijesiti to? geometrijski, to znaci dobiti onu tocku u kojoj se ta dva pravca sijeku
opcenito, znaci dobiti cemu je jednak x, odn y (ovi sa indexima su nam poznati,, to uvrstis prema zadatku, x i y su zbilja nepoznati :) )
pa onda vidis, da su oba zapisana tako da pise y = nesto
pa super, onda kazes, ta dva nesto su jednaka :)
[latex] k_1x + y_1 = k_2x + y_2[/latex]
viiidiii, sad imas samo jednu nepoznanicu :) (to se jos i zove, u prvoj jedznadzbi izrazi jednu nepoznanicu, npr y, preko svih ostalih i taj y trpni u drugu jedznadzbu na sve mjesta gdje pise y :), fkors, ti si biras koja ti je prva a koja druga jednazdba, ako skuzis da negdje imas manje za pisati or smth)
ok, sad vidimo da imamo samo x, pa onda x na jednu, ostalo na drugu stranu
[latex] (k_1 - k_2)x = y_2 - y_1[/latex]
i konacno
[latex] x = \frac{y_2 - y_1}{k_1 - k_2}[/latex]
sad taj x frkemo nazad u jednadzbu iz koje smo ga uzeli (ili u koju nam je zgodnije tutnut ga, ali u neku od onih sa kojima smo poceli, znaci u nasem slucaju one koje su oblika y = nesto)
[latex] y = k_1\frac{y_2 - y_1}{k_1 - k_2} + y_1[/latex]
i u konkretnom slucaju, sad tu trpnes brojeve umjesto ovih koji imaju indexe :)
ako su okomiti, ti svejedno dobijes tocku presjeka na ovaj nacin, a kao dodatni feature je da ces skuziti da su okomiti (pa time i da se sigurno sijeku) je kad uzmes k_1 i k_2 i pomnozis ih... ako dobijes -1, znaci da su okomiti
2. ako ne skuzis da su koeficijenti isti (test moze biti da jednog podijelis s drugim, pa trebas dobiti 1, ili da od jednog oduzmes drugi pa trebas dobiti 0, obicno se oduzimanje svodi na mnozenje jer imamo razlomke... pa ono :) ), radis kao i do sada
znaci imas
[latex]y = k x + y_1[/latex][latex]y = k x + y_2[/latex]
y = nesto
[latex] k x + y_1 = k x + y_2[/latex]
x na jednu, ostalo na drugu stranu
[latex] (k - k) x = y_2 - y_1[/latex]
i konacno
[latex] 0 = y_2 - y_1[/latex]
gdje ovo desno moze biti neki broj razlicit od nule, ali i jednak nuli
ako JE RAZLICIT od nule to znaci da su pravci paralelni (jer izraz 0 = 5 nije istinit :) )
ako pise 0 = 0, to znaci da se radi o istom pravcu (za kojeg je netko bio mastovit i napisao ga na dva nacina :) )
pa ti je to odmah i 3. pitanje :)
anyway, odi u neku malo vecu knjizaru i trazi zute tablice :)
npr mladost, znanje... neke koje imaju skolski pribor :)
ne znam da li smijete imati tablice na maturi, ali kad nadjes dovoljno presjeka, ostat ce ti formule u glavi, vjeruj mi :)
za pocetak, jednadzba pravca je u nekom od oblika: (valjda me nazivi dobro sluze  )
explicitni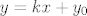 
implicitni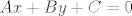 
ono sto ti jos treba, uvijek za znati je jednadzba pravca kroz dvije tocke, namely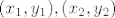 
(edit: ispravljena jdba, pomijesah brojnik i nazivnik  sad je dobro  )
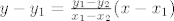
gdje je ovaj razlomak u stvari koeficijent smjera pravca, znaci onaj k iz prvog oblika
y_0 dobijes kad razlomak pomnozis sa x_1 i tome dodas y_1 (no, sredis ovu kobasicu da lijepo pise )
takodjer, pravac se moze zadati kao jos pokoje rjesenje sustava jednadzbi
npr, kao presjek dviju ravnina (onda njihovo rjesenje je pravac, ako se ravnine sijeku; je cijela ravnina ako su ravnine jedna te ista, i nema rjesenja ako su ravnine paralelne)
nisi spominjao 3d i ravnine, ali mozda ti zatreba u nekim zadacima kasnije....
anyway, onda u ovoj svojoj teoriji dodajes jos stanje da su 2 pravca mimosmjerna - nemaju zajednickih tocaka i nisu paralelni
anyway, ova tvoja teorija bez ovog mog paragrafa je 2D, sa mojim paragrafom je 3D, formule se malo prosire
no, za formule, ako nisi do sada, ajd si odi u knjizaru i kupi tzv 'zute tablice', kartonska zuta harmonika koja ima sve formule srednjoskolske matematike na sebi, i korisna je i pod stare dane
cijena bi bila valjda oko 20tak kuna ili tako nesto.... bilo je to davno kad sam to kupovala
ajmo sad na tvoje probleme
zapravo, ajmo jos jednu konverziju
da bi iz implicitnog dobio explicitni (u pravilu cesce baratamo s njime ) hitis y da ostane sam i usamljen na svojoj strani, a ostatak sredis kako spada... namely, dobijes
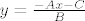 i to sad lijepo sredis (podijelis sa B sto se dijeliti da - rjesis se razlomaka) - ne zaboraviti UVIJEK paziti na predznake !
ok, sad tvoji problemi
1. sijeku se
znaci, imas ova dva cuda
 
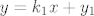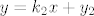
sto znaci rijesiti to? geometrijski, to znaci dobiti onu tocku u kojoj se ta dva pravca sijeku
opcenito, znaci dobiti cemu je jednak x, odn y (ovi sa indexima su nam poznati,, to uvrstis prema zadatku, x i y su zbilja nepoznati )
pa onda vidis, da su oba zapisana tako da pise y = nesto
pa super, onda kazes, ta dva nesto su jednaka
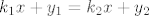
viiidiii, sad imas samo jednu nepoznanicu (to se jos i zove, u prvoj jedznadzbi izrazi jednu nepoznanicu, npr y, preko svih ostalih i taj y trpni u drugu jedznadzbu na sve mjesta gdje pise y , fkors, ti si biras koja ti je prva a koja druga jednazdba, ako skuzis da negdje imas manje za pisati or smth)
ok, sad vidimo da imamo samo x, pa onda x na jednu, ostalo na drugu stranu
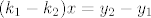
i konacno
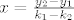
sad taj x frkemo nazad u jednadzbu iz koje smo ga uzeli (ili u koju nam je zgodnije tutnut ga, ali u neku od onih sa kojima smo poceli, znaci u nasem slucaju one koje su oblika y = nesto)
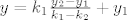
i u konkretnom slucaju, sad tu trpnes brojeve umjesto ovih koji imaju indexe
ako su okomiti, ti svejedno dobijes tocku presjeka na ovaj nacin, a kao dodatni feature je da ces skuziti da su okomiti (pa time i da se sigurno sijeku) je kad uzmes k_1 i k_2 i pomnozis ih... ako dobijes -1, znaci da su okomiti
2. ako ne skuzis da su koeficijenti isti (test moze biti da jednog podijelis s drugim, pa trebas dobiti 1, ili da od jednog oduzmes drugi pa trebas dobiti 0, obicno se oduzimanje svodi na mnozenje jer imamo razlomke... pa ono ), radis kao i do sada
znaci imas
 
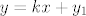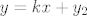
y = nesto
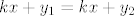
x na jednu, ostalo na drugu stranu
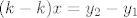
i konacno
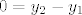
gdje ovo desno moze biti neki broj razlicit od nule, ali i jednak nuli
ako JE RAZLICIT od nule to znaci da su pravci paralelni (jer izraz 0 = 5 nije istinit )
ako pise 0 = 0, to znaci da se radi o istom pravcu (za kojeg je netko bio mastovit i napisao ga na dva nacina )
pa ti je to odmah i 3. pitanje
anyway, odi u neku malo vecu knjizaru i trazi zute tablice
npr mladost, znanje... neke koje imaju skolski pribor
ne znam da li smijete imati tablice na maturi, ali kad nadjes dovoljno presjeka, ostat ce ti formule u glavi, vjeruj mi
Zadnja promjena: Nesi; 20:36 uto, 3. 6. 2008; ukupno mijenjano 1 put.
|
