|
Kako najbrže naći minimalni polinom ako imam zadanu neku kvadratnu matricu?
Naprimjer, recimo da imam 4×4 matricu [latex]\bf{A}[/latex] i da dobijem da je njen karakteristični polinom [latex]k_A (\lambda)=(\lambda-2)^2(\lambda-1)^2[/latex]. E sad, znamo da minimalni polinom može biti nešto od sljedećega:
(i) [latex](\lambda-2)(\lambda-1)[/latex] ili
(ii) [latex](\lambda-2)^2(\lambda-1)[/latex] ili
(iii) [latex](\lambda-2)(\lambda-1)^2[/latex] ili pak
(iv) [latex](\lambda-2)^2(\lambda-1)^2[/latex]
I sad bi krenuli od polinoma najnižeg stupnja i uvrštavali [latex]\bf{A}[/latex] u polinome (i)-(iii) sve dok kao rezultat ne dobijemo nul-matricu (a možemo biti sigurni da ćemo ju dobiti, jer ako ništa drugo, prema Hamilton-Cayleyevom teoremu će matrica sigurno poništiti (iv) pa će minimalni polinom biti jednak karakterističnom, ako nul-matricu ne dobijemo prije).
Mene sad zanima je li to jedini način da dođemo do minimalnog polinoma ili postoji neki brži i elegantniji put? Poput još nekog svojstva koje iskoristimo kako bi došli do rješenja. Jer već u (ii) treba pomnožiti 4×4 matricu [latex]\bf{A}-2\bf{I}[/latex] prvo sa samom sobom a onda i sa [latex]\bf{A-I}[/latex] pa ako se dobije nešto različito od nul-matrice treba ići dalje: oduzimati matrice, potencirati, množiti itd , a da je kojim slučajem karakteristični polinom oblika [latex](\lambda-\lambda_1)^5 \cdots[/latex] onda bi u općenitom slučaju trebali računati petu potenciju matrice [latex]\bf{A}-\lambda_1\bf{I}[/latex] i možda ju još pomnožiti sa 4, 5, 7 drugih matrica, ovisno o tome kako izgleda karakteristični polinom. Dakle: je li opisani način jedini ili do minimalnog polinoma možemo doći i drugačije?
Hvala na pomoći :)
Kako najbrže naći minimalni polinom ako imam zadanu neku kvadratnu matricu?
Naprimjer, recimo da imam 4×4 matricu 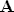 i da dobijem da je njen karakteristični polinom i da dobijem da je njen karakteristični polinom  . E sad, znamo da minimalni polinom može biti nešto od sljedećega: . E sad, znamo da minimalni polinom može biti nešto od sljedećega:
(i) 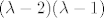 ili ili
(ii) 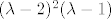 ili ili
(iii) 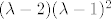 ili pak ili pak
(iv) 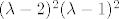
I sad bi krenuli od polinoma najnižeg stupnja i uvrštavali 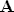 u polinome (i)-(iii) sve dok kao rezultat ne dobijemo nul-matricu (a možemo biti sigurni da ćemo ju dobiti, jer ako ništa drugo, prema Hamilton-Cayleyevom teoremu će matrica sigurno poništiti (iv) pa će minimalni polinom biti jednak karakterističnom, ako nul-matricu ne dobijemo prije). u polinome (i)-(iii) sve dok kao rezultat ne dobijemo nul-matricu (a možemo biti sigurni da ćemo ju dobiti, jer ako ništa drugo, prema Hamilton-Cayleyevom teoremu će matrica sigurno poništiti (iv) pa će minimalni polinom biti jednak karakterističnom, ako nul-matricu ne dobijemo prije).
Mene sad zanima je li to jedini način da dođemo do minimalnog polinoma ili postoji neki brži i elegantniji put? Poput još nekog svojstva koje iskoristimo kako bi došli do rješenja. Jer već u (ii) treba pomnožiti 4×4 matricu 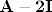 prvo sa samom sobom a onda i sa prvo sa samom sobom a onda i sa 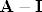 pa ako se dobije nešto različito od nul-matrice treba ići dalje: oduzimati matrice, potencirati, množiti itd , a da je kojim slučajem karakteristični polinom oblika pa ako se dobije nešto različito od nul-matrice treba ići dalje: oduzimati matrice, potencirati, množiti itd , a da je kojim slučajem karakteristični polinom oblika 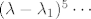 onda bi u općenitom slučaju trebali računati petu potenciju matrice onda bi u općenitom slučaju trebali računati petu potenciju matrice 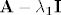 i možda ju još pomnožiti sa 4, 5, 7 drugih matrica, ovisno o tome kako izgleda karakteristični polinom. Dakle: je li opisani način jedini ili do minimalnog polinoma možemo doći i drugačije? i možda ju još pomnožiti sa 4, 5, 7 drugih matrica, ovisno o tome kako izgleda karakteristični polinom. Dakle: je li opisani način jedini ili do minimalnog polinoma možemo doći i drugačije?
Hvala na pomoći 
_________________  |




