| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Lara
Forumaš(ica)


Pridružen/a: 17. 01. 2007. (16:23:54)
Postovi: (53)16
Spol: 
|
 Postano: 17:03 sri, 17. 1. 2007 Naslov: par pitanja u vezi gradiva Postano: 17:03 sri, 17. 1. 2007 Naslov: par pitanja u vezi gradiva |
    |
|
|
Evo prolazim skriptu i kužim da sam malo podcijenila kolegij... pa molim nekog da mi pomogne oko ovih par stvari:
tm.1.79. (Uređajna karakteristika skupa R)
zašto su definirani skupovi L i D nužno oba neprazni?
zašto je P<S?
tm.1.73. (Uređajna karakteristika skupa Q)
kakve veze ima parnost da razmatramo ta dva slučaja kad je n paran i kad je n neparan? jednom iscrpljujemo skup A, jednom skup Q. zašto, kako?
tm.139. Knaster Tarskijev teorem.
dan je primjer skupa čija se egzistencija tvrdi u dokazu.
kako se pokaže da ovaj skup zadovoljava teorem?
str.25.
definirali smo k(A) kao kolekciju svih njemu ekvipotentih skupova. kako se pokaže da to nije skup?
prop.1.14.
nisam baš razumjela zašto je f surjekcija. malo pojašnjenje.
4.str.
kako se pokaže da ovo nisu skupovi, već prave klase. je li to malo teže za pokazati, pa je u tome problem?
nadam se da netko ima volje, znanja i vremena...
Evo prolazim skriptu i kužim da sam malo podcijenila kolegij... pa molim nekog da mi pomogne oko ovih par stvari:
tm.1.79. (Uređajna karakteristika skupa R)
zašto su definirani skupovi L i D nužno oba neprazni?
zašto je P<S?
tm.1.73. (Uređajna karakteristika skupa Q)
kakve veze ima parnost da razmatramo ta dva slučaja kad je n paran i kad je n neparan? jednom iscrpljujemo skup A, jednom skup Q. zašto, kako?
tm.139. Knaster Tarskijev teorem.
dan je primjer skupa čija se egzistencija tvrdi u dokazu.
kako se pokaže da ovaj skup zadovoljava teorem?
str.25.
definirali smo k(A) kao kolekciju svih njemu ekvipotentih skupova. kako se pokaže da to nije skup?
prop.1.14.
nisam baš razumjela zašto je f surjekcija. malo pojašnjenje.
4.str.
kako se pokaže da ovo nisu skupovi, već prave klase. je li to malo teže za pokazati, pa je u tome problem?
nadam se da netko ima volje, znanja i vremena...
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 20:56 sri, 17. 1. 2007 Naslov: Re: par pitanja u vezi gradiva Postano: 20:56 sri, 17. 1. 2007 Naslov: Re: par pitanja u vezi gradiva |
    |
|
|
[quote="Lara"]
tm.1.79. (Uređajna karakteristika skupa R)
zašto su definirani skupovi L i D nužno oba neprazni?
[/quote]
[latex]L=\{y\in M_1 \mid y < x_0\}[/latex].
Kako [latex]S_1[/latex] nema najmanji element, onda postoji neki [latex]s\in S_1[/latex] takav da je [latex]s < x_0[/latex], a kako je [latex]M_1[/latex] gust u [latex]S_1[/latex] mora postojati neki [latex]m\in M_1[/latex] takav da je [latex]s<m<x_0[/latex]. Ocito je [latex]m\in L[/latex].
Analogno se dokazuje da je skup D neprazan.
[quote]
zašto je P<S?
[/quote]
Zato sto u suprotnom ne bi imali neprazan presjek, a pretpostavljeno je da imaju neprazan presjek.
[quote]
tm.1.73. (Uređajna karakteristika skupa Q)
kakve veze ima parnost da razmatramo ta dva slučaja kad je n paran i kad je n neparan? jednom iscrpljujemo skup A, jednom skup Q. zašto, kako?
[/quote]
Taj postupak sluzi da osiguramo da ce konstruirana funkcija cuvati uredjaj i biti bijekcija.
[quote]
tm.139. Knaster Tarskijev teorem.
dan je primjer skupa čija se egzistencija tvrdi u dokazu.
kako se pokaže da ovaj skup zadovoljava teorem?
[/quote]
Vidi teorem 1.65 i korolar 1.66 :wink:
[quote]
str.25.
definirali smo k(A) kao kolekciju svih njemu ekvipotentih skupova. kako se pokaže da to nije skup?
[/quote]
Neka je [latex]A[/latex] proizvoljan neprazan skup.
Neka je [latex]B=\{X \mid X \sim A\}[/latex]
Pretpostavimo da je [latex]B[/latex] skup. Tada je i [latex]\mathcal{P}(B)[/latex] takodjer skup.
Za svaki [latex]x \in \mathcal{P}(B)[/latex] definiramo [latex]A_x=A \times \{x\}[/latex].
Ocito za svaki [latex]x \in \mathcal{P}(B)[/latex] postoji bijekcija izmedju [latex]A[/latex] i [latex]A_x[/latex]. To znaci da je [latex]A_x \in \mathcal{P}(B)[/latex] za sve [latex]x \in \mathcal{P}(B)[/latex].
Tada postoji injekcija sa [latex]\mathcal{P}(B)[/latex] u [latex]B[/latex], a to je kontradikcija s Cantorovim osnovnim teoremom.
Obrati pozornost da to zapravo znaci da nije dobro na taj nacin definirati kardinalne brojeve.
[quote]
prop.1.14.
nisam baš razumjela zašto je f surjekcija. malo pojašnjenje.
[/quote]
Ne znam kako da to na forumu napisem jasnije nego sto pise u skripti. :-k
Uhvati me nakon vjezbi ili kad me vidis na faksu da to rijesimo.
[quote]
4.str.
kako se pokaže da ovo nisu skupovi, već prave klase. je li to malo teže za pokazati, pa je u tome problem?
[/quote]
Redom:
- vidi gore dokaz da to nije klasa za bilo koji neprazan skup, a ne samo za [latex]\mathbb{N}[/latex]
- tada bi i klasa ordinalnih brojeva bila skup
- preko Zornove leme pokaze se da se na svakom skupu moze definirati grupa.
| Lara (napisa): |
tm.1.79. (Uređajna karakteristika skupa R)
zašto su definirani skupovi L i D nužno oba neprazni?
|
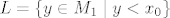 . .
Kako 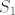 nema najmanji element, onda postoji neki nema najmanji element, onda postoji neki 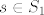 takav da je takav da je 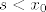 , a kako je , a kako je 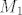 gust u gust u 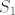 mora postojati neki mora postojati neki 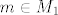 takav da je takav da je 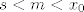 . Ocito je . Ocito je 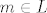 . .
Analogno se dokazuje da je skup D neprazan.
Zato sto u suprotnom ne bi imali neprazan presjek, a pretpostavljeno je da imaju neprazan presjek.
| Citat: |
tm.1.73. (Uređajna karakteristika skupa Q)
kakve veze ima parnost da razmatramo ta dva slučaja kad je n paran i kad je n neparan? jednom iscrpljujemo skup A, jednom skup Q. zašto, kako?
|
Taj postupak sluzi da osiguramo da ce konstruirana funkcija cuvati uredjaj i biti bijekcija.
| Citat: |
tm.139. Knaster Tarskijev teorem.
dan je primjer skupa čija se egzistencija tvrdi u dokazu.
kako se pokaže da ovaj skup zadovoljava teorem?
|
Vidi teorem 1.65 i korolar 1.66 
| Citat: |
str.25.
definirali smo k(A) kao kolekciju svih njemu ekvipotentih skupova. kako se pokaže da to nije skup?
|
Neka je  proizvoljan neprazan skup. proizvoljan neprazan skup.
Neka je 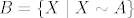
Pretpostavimo da je  skup. Tada je i skup. Tada je i 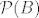 takodjer skup. takodjer skup.
Za svaki 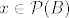 definiramo definiramo 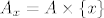 . .
Ocito za svaki 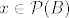 postoji bijekcija izmedju postoji bijekcija izmedju  i i 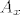 . To znaci da je . To znaci da je 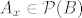 za sve za sve 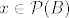 . .
Tada postoji injekcija sa 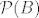 u u  , a to je kontradikcija s Cantorovim osnovnim teoremom. , a to je kontradikcija s Cantorovim osnovnim teoremom.
Obrati pozornost da to zapravo znaci da nije dobro na taj nacin definirati kardinalne brojeve.
| Citat: |
prop.1.14.
nisam baš razumjela zašto je f surjekcija. malo pojašnjenje.
|
Ne znam kako da to na forumu napisem jasnije nego sto pise u skripti. 
Uhvati me nakon vjezbi ili kad me vidis na faksu da to rijesimo.
| Citat: |
4.str.
kako se pokaže da ovo nisu skupovi, već prave klase. je li to malo teže za pokazati, pa je u tome problem?
|
Redom:
- vidi gore dokaz da to nije klasa za bilo koji neprazan skup, a ne samo za 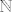
- tada bi i klasa ordinalnih brojeva bila skup
- preko Zornove leme pokaze se da se na svakom skupu moze definirati grupa.
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
Lara
Forumaš(ica)


Pridružen/a: 17. 01. 2007. (16:23:54)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
 Postano: 9:06 pon, 5. 2. 2007 Naslov: Postano: 9:06 pon, 5. 2. 2007 Naslov: |
    |
|
|
Imam jedno pitanje u vezi gradiva. Nisam bio na zadnja 3 predavanja (jedno zbog kolokvija, 2 zbog bolesti :( - tek toliko da se opravdam :D), pa me zanima samo ugrubo šta smo radili. Ne tražim nekakav detaljni izvještaj, samo ako se nekome da navesti što nismo detaljno obradili čisto informativno, jer sumnjam da smo stigli u 3 predavanja napraviti detaljno 30 stranica.
Zadnje predavanje na kojem sam bio je ono na kojem smo počeli ordinalne brojeve i napravili do 62., 63. str.
Unaprijed hvala na odgovoru :wave:
Imam jedno pitanje u vezi gradiva. Nisam bio na zadnja 3 predavanja (jedno zbog kolokvija, 2 zbog bolesti  - tek toliko da se opravdam - tek toliko da se opravdam  ), pa me zanima samo ugrubo šta smo radili. Ne tražim nekakav detaljni izvještaj, samo ako se nekome da navesti što nismo detaljno obradili čisto informativno, jer sumnjam da smo stigli u 3 predavanja napraviti detaljno 30 stranica. ), pa me zanima samo ugrubo šta smo radili. Ne tražim nekakav detaljni izvještaj, samo ako se nekome da navesti što nismo detaljno obradili čisto informativno, jer sumnjam da smo stigli u 3 predavanja napraviti detaljno 30 stranica.
Zadnje predavanje na kojem sam bio je ono na kojem smo počeli ordinalne brojeve i napravili do 62., 63. str.
Unaprijed hvala na odgovoru 
|
|
| [Vrh] |
|
koryanshea
Forumaš(ica)


Pridružen/a: 12. 10. 2003. (23:50:23)
Postovi: (442)16
Spol: 
Lokacija: Bebop (converted interplanetary trawler)
|
 Postano: 11:32 čet, 15. 2. 2007 Naslov: Postano: 11:32 čet, 15. 2. 2007 Naslov: |
    |
|
|
kao da nitko nije bio na sva tri zadnja predavanja 0_o
meni treba netko tko je bio na predzadnjem - kad su se definirale operacije na ordinalnim brojevima. zanima me samo koji su se teoremi dokazivali, jesu li se dokazivale leme o ordinalnom broju uređene sume i produkta dus-ova, treba li ucit dokaz logaritamskog algoritma i tm-a o normalnoj formi?
kao da nitko nije bio na sva tri zadnja predavanja 0_o
meni treba netko tko je bio na predzadnjem - kad su se definirale operacije na ordinalnim brojevima. zanima me samo koji su se teoremi dokazivali, jesu li se dokazivale leme o ordinalnom broju uređene sume i produkta dus-ova, treba li ucit dokaz logaritamskog algoritma i tm-a o normalnoj formi?
_________________  "Download the files to a non-networked, firewalled computer."
- Dr. Elizabeth Weir |
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 12:12 čet, 15. 2. 2007 Naslov: Postano: 12:12 čet, 15. 2. 2007 Naslov: |
    |
|
|
[quote="koryanshea"]kao da nitko nije bio na sva tri zadnja predavanja 0_o
meni treba netko tko je bio na predzadnjem - kad su se definirale operacije na ordinalnim brojevima. zanima me samo koji su se teoremi dokazivali, jesu li se dokazivale leme o ordinalnom broju uređene sume i produkta dus-ova, treba li ucit dokaz logaritamskog algoritma i tm-a o normalnoj formi?[/quote]
Ja sam bio na sva tri zadnja. :)
Ovo koje tebe zanima je bilo 30.1. Evo ukratko što smo radili:
[list]
[*]Dokazali smo teorem rekurzije (svodi se na primjenu općeg teorema rekurzije čija je skica dokaza dana na predavanju od 23.1.).
[*]Primijenili smo teorem rekurzije da definiramo kumulativnu hijerarhiju.
[*]Definirali smo zbrajanje ordinalnih brojeva, iskazali spomenutu lemu o uređenoj sumi bez dokaza i dokazali asocijativnost zbrajanja ordinalnih brojeva transfinitnom indukcijom (ostala svojstva smo izlistali).
[*]Definirali smo množenje ordinalnih brojeva, opet iskazali lemu o uređenom produktu bez dokaza i izlistali svojstva množenja.
[*]Definirali potenciranje, izlistali svojstva...
[*]Iskazali i dokazali (doduše ne baš do najsitnijih detalja) teoreme o oduzimanju, dijeljenju s ostatkom, logaritamski algoritam i teorem o normalnoj formi.
[*]Komentirali, napominjali, prisjećali se kardinalnosti, definirali kardinalan broj.
[/list:u]
Eto, sad usporedi sa skriptom. :)
| koryanshea (napisa): | kao da nitko nije bio na sva tri zadnja predavanja 0_o
meni treba netko tko je bio na predzadnjem - kad su se definirale operacije na ordinalnim brojevima. zanima me samo koji su se teoremi dokazivali, jesu li se dokazivale leme o ordinalnom broju uređene sume i produkta dus-ova, treba li ucit dokaz logaritamskog algoritma i tm-a o normalnoj formi? |
Ja sam bio na sva tri zadnja. 
Ovo koje tebe zanima je bilo 30.1. Evo ukratko što smo radili:
- Dokazali smo teorem rekurzije (svodi se na primjenu općeg teorema rekurzije čija je skica dokaza dana na predavanju od 23.1.).
- Primijenili smo teorem rekurzije da definiramo kumulativnu hijerarhiju.
- Definirali smo zbrajanje ordinalnih brojeva, iskazali spomenutu lemu o uređenoj sumi bez dokaza i dokazali asocijativnost zbrajanja ordinalnih brojeva transfinitnom indukcijom (ostala svojstva smo izlistali).
- Definirali smo množenje ordinalnih brojeva, opet iskazali lemu o uređenom produktu bez dokaza i izlistali svojstva množenja.
- Definirali potenciranje, izlistali svojstva...
- Iskazali i dokazali (doduše ne baš do najsitnijih detalja) teoreme o oduzimanju, dijeljenju s ostatkom, logaritamski algoritam i teorem o normalnoj formi.
- Komentirali, napominjali, prisjećali se kardinalnosti, definirali kardinalan broj.
Eto, sad usporedi sa skriptom. 
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
 Postano: 12:18 pon, 19. 2. 2007 Naslov: Postano: 12:18 pon, 19. 2. 2007 Naslov: |
    |
|
|
Eto, imam jedno pitanje.
Radi se o lemi prije dokaza teorama o rekurziji (zapravo prije iskaza općeg tm-a o rekurziji). Glasi ovako:
Neka je A neka [b]klasa[/b] i < dobar uređaj na A. Ako a iz A nije najveći element tada za a postoji neposredni sljedbenik.
[i][u]Dokaz:[/u][/i]
Pošto a nije najveći element tada je B={y iz A:a<y} neprazan [b]podskup[/b] od A. Tada je najmanji element od B neposredni sljedbenik od a.
E sad, nije mi jasno zašto bi B bio skup (ako je poskup od A onda je očito skup). Ne možemo preko sheme aksioma separacije jer A nije skup a čini mi se i da općenito nemamo garancije da je B skup :-k Zbunjen sam :silly:
I još, kad (ako) to pitanje rasčistimo, neposredni sljedbenik od a (u A) je onaj ordinalni broj b iz A za koji ne postoji c iz A takav da a<c<b, ne? Tako mi se čini logično ali pitam jer zapravo nigdje nismo definirali...
Zahvaljujem unaprijed na odgovoru :D
Eto, imam jedno pitanje.
Radi se o lemi prije dokaza teorama o rekurziji (zapravo prije iskaza općeg tm-a o rekurziji). Glasi ovako:
Neka je A neka klasa i < dobar uređaj na A. Ako a iz A nije najveći element tada za a postoji neposredni sljedbenik.
Dokaz:
Pošto a nije najveći element tada je B={y iz A:a<y} neprazan podskup od A. Tada je najmanji element od B neposredni sljedbenik od a.
E sad, nije mi jasno zašto bi B bio skup (ako je poskup od A onda je očito skup). Ne možemo preko sheme aksioma separacije jer A nije skup a čini mi se i da općenito nemamo garancije da je B skup  Zbunjen sam Zbunjen sam 
I još, kad (ako) to pitanje rasčistimo, neposredni sljedbenik od a (u A) je onaj ordinalni broj b iz A za koji ne postoji c iz A takav da a<c<b, ne? Tako mi se čini logično ali pitam jer zapravo nigdje nismo definirali...
Zahvaljujem unaprijed na odgovoru 
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 13:10 pon, 19. 2. 2007 Naslov: Postano: 13:10 pon, 19. 2. 2007 Naslov: |
    |
|
|
[quote="vili"]Pošto a nije najveći element tada je B={y iz A:a<y} neprazan [b]podskup[/b] od A. Tada je najmanji element od B neposredni sljedbenik od a.[/quote]
Da, to i mene zbunjuje. A slična stvar je na dva mjesta u dokazu općeg teorema rekurzije. Prvo, kod tvrdnje 2. se definira klasa B={a@A : ne postoji g@G td. Dom(g)=p_A(a)} i iz nekog razloga je očito da je to skup. :? A pri kraju dokaza za klasu B={a@A : fi(a)!=ksi(a)} isto kaže da je očito skup. :?
[quote="vili"]I još, kad (ako) to pitanje rasčistimo, neposredni sljedbenik od a (u A) je onaj ordinalni broj b iz A za koji ne postoji c iz A takav da a<c<b, ne? Tako mi se čini logično ali pitam jer zapravo nigdje nismo definirali...[/quote]
To bi bilo to, da. Mislim da se u nekim dokazima upravo takva definicija koristi.
| vili (napisa): | | Pošto a nije najveći element tada je B={y iz A:a<y} neprazan podskup od A. Tada je najmanji element od B neposredni sljedbenik od a. |
Da, to i mene zbunjuje. A slična stvar je na dva mjesta u dokazu općeg teorema rekurzije. Prvo, kod tvrdnje 2. se definira klasa B={a@A : ne postoji g@G td. Dom(g)=p_A(a)} i iz nekog razloga je očito da je to skup.  A pri kraju dokaza za klasu B={a@A : fi(a)!=ksi(a)} isto kaže da je očito skup. A pri kraju dokaza za klasu B={a@A : fi(a)!=ksi(a)} isto kaže da je očito skup. 
| vili (napisa): | | I još, kad (ako) to pitanje rasčistimo, neposredni sljedbenik od a (u A) je onaj ordinalni broj b iz A za koji ne postoji c iz A takav da a<c<b, ne? Tako mi se čini logično ali pitam jer zapravo nigdje nismo definirali... |
To bi bilo to, da. Mislim da se u nekim dokazima upravo takva definicija koristi.
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
 Postano: 13:22 pon, 19. 2. 2007 Naslov: Postano: 13:22 pon, 19. 2. 2007 Naslov: |
    |
|
|
[quote="Melkor"][quote="vili"]Pošto a nije najveći element tada je B={y iz A:a<y} neprazan [b]podskup[/b] od A. Tada je najmanji element od B neposredni sljedbenik od a.[/quote]
Da, to i mene zbunjuje. A slična stvar je na dva mjesta u dokazu općeg teorema rekurzije. Prvo, kod tvrdnje 2. se definira klasa B={a@A : ne postoji g@G td. Dom(g)=p_A(a)} i iz nekog razloga je očito da je to skup. :? A pri kraju dokaza za klasu B={a@A : fi(a)!=ksi(a)} isto kaže da je očito skup. :?
[/quote]
Da, primjetio sam i ja baš ta dva slučaja upravo kad sam detaljno prolazio dokaz, ali nisam htio više post-ati jer je argument (nadam se da postoji :shock:) da su to skupovi vjerojatno isti.
Dakle, :krcko: (Trebalo bi napravit ovaj "smajli" bez Krcka, kao službeni poziv upomoć :mrgreen:)
U ovom konkretnom slučaju se nadam da će mdoko doletit i spasit nas :superman:
| Melkor (napisa): | | vili (napisa): | | Pošto a nije najveći element tada je B={y iz A:a<y} neprazan podskup od A. Tada je najmanji element od B neposredni sljedbenik od a. |
Da, to i mene zbunjuje. A slična stvar je na dva mjesta u dokazu općeg teorema rekurzije. Prvo, kod tvrdnje 2. se definira klasa B={a@A : ne postoji g@G td. Dom(g)=p_A(a)} i iz nekog razloga je očito da je to skup.  A pri kraju dokaza za klasu B={a@A : fi(a)!=ksi(a)} isto kaže da je očito skup. A pri kraju dokaza za klasu B={a@A : fi(a)!=ksi(a)} isto kaže da je očito skup. 
|
Da, primjetio sam i ja baš ta dva slučaja upravo kad sam detaljno prolazio dokaz, ali nisam htio više post-ati jer je argument (nadam se da postoji  ) da su to skupovi vjerojatno isti. ) da su to skupovi vjerojatno isti.
Dakle,  (Trebalo bi napravit ovaj "smajli" bez Krcka, kao službeni poziv upomoć (Trebalo bi napravit ovaj "smajli" bez Krcka, kao službeni poziv upomoć  ) )
U ovom konkretnom slučaju se nadam da će mdoko doletit i spasit nas 
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 17:04 pon, 19. 2. 2007 Naslov: Postano: 17:04 pon, 19. 2. 2007 Naslov: |
    |
|
|
[quote="Melkor"]
Da, to i mene zbunjuje. A slična stvar je na dva mjesta u dokazu općeg teorema rekurzije. Prvo, kod tvrdnje 2. se definira klasa B={a@A : ne postoji g@G td. Dom(g)=p_A(a)} i iz nekog razloga je očito da je to skup. :? A pri kraju dokaza za klasu B={a@A : fi(a)!=ksi(a)} isto kaže da je očito skup. :?[/quote]
Sad sam pogledao u skriptu, i iskreno, na prvi pogled ni ja ne vidim zasto bi to morali biti skupovi, ali isto tako, koliko ja vidim nije ni bitno jesu li te klase skupovi, nego je bitno da ako su neprazne, onda imaju najmanji element, a to slijedi iz cinjenice da je < dobar uredjaj.
P.S. Ovo je ksi: [latex]\xi[/latex], a ovo [latex]\psi[/latex] je psi. :cool:
| Melkor (napisa): |
Da, to i mene zbunjuje. A slična stvar je na dva mjesta u dokazu općeg teorema rekurzije. Prvo, kod tvrdnje 2. se definira klasa B={a@A : ne postoji g@G td. Dom(g)=p_A(a)} i iz nekog razloga je očito da je to skup.  A pri kraju dokaza za klasu B={a@A : fi(a)!=ksi(a)} isto kaže da je očito skup. A pri kraju dokaza za klasu B={a@A : fi(a)!=ksi(a)} isto kaže da je očito skup.  |
Sad sam pogledao u skriptu, i iskreno, na prvi pogled ni ja ne vidim zasto bi to morali biti skupovi, ali isto tako, koliko ja vidim nije ni bitno jesu li te klase skupovi, nego je bitno da ako su neprazne, onda imaju najmanji element, a to slijedi iz cinjenice da je < dobar uredjaj.
P.S. Ovo je ksi: 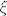 , a ovo , a ovo 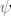 je psi. je psi. 
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
 Postano: 17:05 pon, 19. 2. 2007 Naslov: Postano: 17:05 pon, 19. 2. 2007 Naslov: |
    |
|
|
[quote="mdoko"][quote="vili"]
[i][u]Dokaz:[/u][/i]
Pošto a nije najveći element tada je B={y iz A:a<y} neprazan [b]podskup[/b] od A. Tada je najmanji element od B neposredni sljedbenik od a.
E sad, nije mi jasno zašto bi B bio skup (ako je poskup od A onda je očito skup). Ne možemo preko sheme aksioma separacije jer A nije skup a čini mi se i da općenito nemamo garancije da je B skup :-k Zbunjen sam :silly:
[/quote]
Nisam zavirio u skriptu, ali mi se cini da se radi o misstypeu tj. da umjesto [i]podskup[/i] treba stajati [i]podklasa[/i] i onda je sve OK. :cool:[/quote]
Pa i nije baš, jer je po definiciji parcijalni uređaj < na klasi A dobar uređaj ako za svaki neprazan [b]podskup[/b] B od A (još je profesor naglasio da je tu podskup a ne podklasa) B sadrži najmanji element.
A u općem teoremu rekurzije je < dobar uređaj na klasi A, tako da ako se radi o podklasi B onda ne znamo da B ima najmanji element :?
EDIT: Ovo sam postao prije nego sam vidio zadnji post, ali i dalje nije dobro zbog gornjeg argumenta (definicija).
| mdoko (napisa): | | vili (napisa): |
Dokaz:
Pošto a nije najveći element tada je B={y iz A:a<y} neprazan podskup od A. Tada je najmanji element od B neposredni sljedbenik od a.
E sad, nije mi jasno zašto bi B bio skup (ako je poskup od A onda je očito skup). Ne možemo preko sheme aksioma separacije jer A nije skup a čini mi se i da općenito nemamo garancije da je B skup  Zbunjen sam Zbunjen sam 
|
Nisam zavirio u skriptu, ali mi se cini da se radi o misstypeu tj. da umjesto podskup treba stajati podklasa i onda je sve OK.  |
Pa i nije baš, jer je po definiciji parcijalni uređaj < na klasi A dobar uređaj ako za svaki neprazan podskup B od A (još je profesor naglasio da je tu podskup a ne podklasa) B sadrži najmanji element.
A u općem teoremu rekurzije je < dobar uređaj na klasi A, tako da ako se radi o podklasi B onda ne znamo da B ima najmanji element 
EDIT: Ovo sam postao prije nego sam vidio zadnji post, ali i dalje nije dobro zbog gornjeg argumenta (definicija).
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
Ante
Forumaš(ica)
Pridružen/a: 17. 02. 2006. (11:12:00)
Postovi: (155)16
Spol: 
|
 Postano: 12:10 ned, 4. 3. 2007 Naslov: Postano: 12:10 ned, 4. 3. 2007 Naslov: |
    |
|
|
muci me jedna recenica na str 66. u skripti prof. Vukovica :bigcry:
dakle, nakon sto dokazemo opci teorem rekurzije, njegovom primjenom ide teorem rekurzije... zasto postoji ona zadnja recenica u tom dokazu: "Lako je vidjeti da je funkcija fi jedinstvena."?
pa sto to ne slijedi iz opceg teorema rekurzije, ali bas u potpunosti?
(a i pise koji red iznad da slijedi) :valjalo: :noidea:
muci me jedna recenica na str 66. u skripti prof. Vukovica 
dakle, nakon sto dokazemo opci teorem rekurzije, njegovom primjenom ide teorem rekurzije... zasto postoji ona zadnja recenica u tom dokazu: "Lako je vidjeti da je funkcija fi jedinstvena."?
pa sto to ne slijedi iz opceg teorema rekurzije, ali bas u potpunosti?
(a i pise koji red iznad da slijedi)  
_________________
Eat a lot, sleep a lot, brush 'em like crazy.
Run a lot, do a lot, never be lazy.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 9:04 pet, 27. 6. 2008 Naslov: Postano: 9:04 pet, 27. 6. 2008 Naslov: |
    |
|
|
Aksiom dobre utemeljenosti (AF):
[latex]\forall x\big(x\neq\emptyset\rightarrow\exists y(y\in x\land y\cap x=\emptyset)\big)[/latex]
Primjer je bilo koji neprazan skup. Npr. pogledajmo [latex]x=\big\{\emptyset,\{\emptyset\}\big\}[/latex].
Prvo primijeti da je [latex]\{\emptyset\}\in x[/latex] i da je [latex]\{\emptyset\}\cap x=\{\emptyset\}\neq \emptyset[/latex]. No zato je [latex]\emptyset\in x[/latex], a [latex]\emptyset\cap x=\emptyset[/latex] pa je AF zadovoljen.
Recimo da maknemo [latex]\emptyset[/latex], tj. gledamo [latex]x'=\big\{\{\emptyset\}\big\}[/latex]. Još uvijek imamo [latex]\{\emptyset\}\in x'[/latex], ali sad je [latex]\{\emptyset\}\cap x'=\emptyset[/latex] pa je opet AF zadovoljen.
Ono što tebe vjerojatno zbunjuje je što si nekako predočavaš da se za [latex]y\in x[/latex] gleda je li [latex]\{y\}\cap x=\emptyset[/latex], što naravno nije. Uoči razliku između toga i [latex]y\cap x=\emptyset[/latex]. U ovom drugom se gledaju [latex]y[/latex]-ovi elementi i nalazi li se koji od njih u [latex]x[/latex]. Za to uopće nema veze što je [latex]y\in x[/latex].
Za kraj, evo kako se AF može iskoristiti da se dokaže [latex]\forall x(x\notin x)[/latex]. Za skup [latex]x[/latex] je prema aksiomu para [latex]\{x\}[/latex] skup. Sad prema AF-u postoji [latex]y\in\{x\}[/latex] takav da je [latex]y\cap\{x\}=\emptyset[/latex]. Naravno, jedina mogućnost za [latex]y[/latex] je [latex]y=x[/latex]. Prema tome, [latex]x\cap\{x\}=\emptyset[/latex]. To znači da se nijedan element desnog skupa ne nalazi u lijevom, tj. [latex]x\notin x[/latex].
Aksiom dobre utemeljenosti (AF):
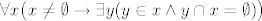
Primjer je bilo koji neprazan skup. Npr. pogledajmo 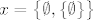 . .
Prvo primijeti da je 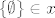 i da je i da je 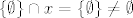 . No zato je . No zato je 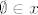 , a , a 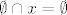 pa je AF zadovoljen. pa je AF zadovoljen.
Recimo da maknemo  , tj. gledamo , tj. gledamo 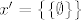 . Još uvijek imamo . Još uvijek imamo 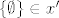 , ali sad je , ali sad je 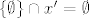 pa je opet AF zadovoljen. pa je opet AF zadovoljen.
Ono što tebe vjerojatno zbunjuje je što si nekako predočavaš da se za 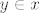 gleda je li gleda je li 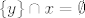 , što naravno nije. Uoči razliku između toga i , što naravno nije. Uoči razliku između toga i 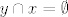 . U ovom drugom se gledaju . U ovom drugom se gledaju  -ovi elementi i nalazi li se koji od njih u -ovi elementi i nalazi li se koji od njih u  . Za to uopće nema veze što je . Za to uopće nema veze što je 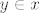 . .
Za kraj, evo kako se AF može iskoristiti da se dokaže 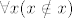 . Za skup . Za skup  je prema aksiomu para je prema aksiomu para 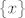 skup. Sad prema AF-u postoji skup. Sad prema AF-u postoji 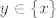 takav da je takav da je 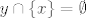 . Naravno, jedina mogućnost za . Naravno, jedina mogućnost za  je je 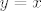 . Prema tome, . Prema tome, 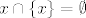 . To znači da se nijedan element desnog skupa ne nalazi u lijevom, tj. . To znači da se nijedan element desnog skupa ne nalazi u lijevom, tj. 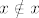 . .
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
Lutajuci
Gost
|
 Postano: 14:43 sub, 6. 9. 2008 Naslov: Potpitanje Postano: 14:43 sub, 6. 9. 2008 Naslov: Potpitanje |
    |
|
|
Melkore, potpitanje od jednog neslušača TS, skroz laičko: što ako u navedenom iskazu AF y nije skup? Kako naime odrediti presjek skupa i nečega što nije skup? Npr, što ako je x={1,2} i y=2: što je presjek x i y? Nisam siguran da je skroz korektno reći: aha, presjek nije definiran, pa je prazan skup: bilo bi to nekako kao da u "običnoj" aritmetici kažmo: plava+3 nije definirano (jer plava nije broj), pa ćemo staviti da je rezultat nula. Unaprijed hvala.
Melkore, potpitanje od jednog neslušača TS, skroz laičko: što ako u navedenom iskazu AF y nije skup? Kako naime odrediti presjek skupa i nečega što nije skup? Npr, što ako je x={1,2} i y=2: što je presjek x i y? Nisam siguran da je skroz korektno reći: aha, presjek nije definiran, pa je prazan skup: bilo bi to nekako kao da u "običnoj" aritmetici kažmo: plava+3 nije definirano (jer plava nije broj), pa ćemo staviti da je rezultat nula. Unaprijed hvala.
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 19:13 sub, 6. 9. 2008 Naslov: Postano: 19:13 sub, 6. 9. 2008 Naslov: |
    |
|
|
@Lutajući: Malo je teže to objasniti ako nisi slušao Matematičku logiku. Ugrubo: standardni objekti teorije skupova su skupovi i samo skupovi. Tako taj y ne može predstavljati ništa drugo nego skup.
Za neke skupove uvode se specijalne oznake koje nisu ništa drugo nego pokrate. Tako je primjerice:
[latex]
\begin{aligned}
0 &:= \emptyset \\
1 &:= \{0\}=\{\emptyset\} \\
2 &:= \{0,1\}=\{\emptyset,\{\emptyset\}\} \\
\end{aligned}
[/latex]
i tako dalje. U tom smislu je onda [latex]\{1,2\}\cap 2=\{1,2\}\cap\{0,1\}=\{1\}[/latex].
Slično, standardni objekti "obične" aritmetike su prirodni brojevi. Standardna interpretacija znaka + u "običnoj" aritmetici je funkcija zbrajanja prirodnih brojeva. Riječ plava nema nikakvu interpretaciju u toj teoriji i stoga izraz plava+3 također nema nikakvu interpretaciju, tj. besmislen je. Nećemo mu pridijeliti nikakvo značenje (nećemo reći da je to nula) dok god ne kažemo što znači plava u okviru teorije.
@Lutajući: Malo je teže to objasniti ako nisi slušao Matematičku logiku. Ugrubo: standardni objekti teorije skupova su skupovi i samo skupovi. Tako taj y ne može predstavljati ništa drugo nego skup.
Za neke skupove uvode se specijalne oznake koje nisu ništa drugo nego pokrate. Tako je primjerice:
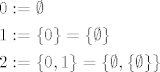
i tako dalje. U tom smislu je onda 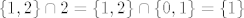 . .
Slično, standardni objekti "obične" aritmetike su prirodni brojevi. Standardna interpretacija znaka + u "običnoj" aritmetici je funkcija zbrajanja prirodnih brojeva. Riječ plava nema nikakvu interpretaciju u toj teoriji i stoga izraz plava+3 također nema nikakvu interpretaciju, tj. besmislen je. Nećemo mu pridijeliti nikakvo značenje (nećemo reći da je to nula) dok god ne kažemo što znači plava u okviru teorije.
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
|






















