| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
5ra
Forumaš(ica)


Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 17:04 pet, 20. 6. 2008 Naslov: Postano: 17:04 pet, 20. 6. 2008 Naslov: |
    |
|
|
Možda ovak:
<nzm(x,y)> = { m*z, z iz Z, m=nzm(x,y)}
pošto je m nzm(x,y) onda postoje n1 i n2 iz Z t.d. x=m*n1, y=m*n2.
Sad uzmemo neki element N iz <nzm(x,y)>. On je oblika m*n3 za neki n3 iz Z. Za N iz tog skupa, je i 2*n1*n2*N unutra (i također proizvoljan).
Pa je 2*n1*n2*N = 2*m*n3*n1*n2 = m*n3*n1*n2 + m*n3*n1*n2 = x*n2*n3 + y*n1*n3 = (n2*n3)x + (n1*n3)y. A to je iz <x>+<y>
:D
Možda ovak:
<nzm(x,y)> = { m*z, z iz Z, m=nzm(x,y)}
pošto je m nzm(x,y) onda postoje n1 i n2 iz Z t.d. x=m*n1, y=m*n2.
Sad uzmemo neki element N iz <nzm(x,y)>. On je oblika m*n3 za neki n3 iz Z. Za N iz tog skupa, je i 2*n1*n2*N unutra (i također proizvoljan).
Pa je 2*n1*n2*N = 2*m*n3*n1*n2 = m*n3*n1*n2 + m*n3*n1*n2 = x*n2*n3 + y*n1*n3 = (n2*n3)x + (n1*n3)y. A to je iz <x>+<y>

_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
rhiannon
Forumaš(ica)

Pridružen/a: 11. 06. 2007. (20:34:03)
Postovi: (D)16
|
|
| [Vrh] |
|
teh_pwnerer
Forumaš(ica)
Pridružen/a: 02. 02. 2006. (19:06:27)
Postovi: (62)16
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
SvekY
Forumaš(ica)


Pridružen/a: 21. 11. 2003. (23:44:22)
Postovi: (FF)16
Spol: 
Lokacija: unitarni vektorski prostor
|
 Postano: 10:56 pon, 23. 6. 2008 Naslov: Re: ideali- teorija Postano: 10:56 pon, 23. 6. 2008 Naslov: Re: ideali- teorija |
    |
|
|
[quote="5ra"]Ako imamo skup cijelih brojeva Z, kako dokazati da je <x>+<y>=<nzm(x,y)>. jedan smjer mi jasan, ali ovaj da je <nzm(x,y)> podskup od <x>+<y> nemogu dobiti.
to je zadatak 16 u skripti. jel zna netko?
:beg:[/quote]
Za smjer dokaza koji je 5ra-u jasan, imam nekih pitanja.
Dakle, dokaz za [latex]\langle x \rangle + \langle y \rangle \subseteq \langle x+y \rangle[/latex]
Koliko detaljno to treba? Pretpostavljam da se koristi ona tvrdnja:
[latex] \forall x,y \in \mathbb{Z} \ \exists n,m \in \mathbb{Z} \ td. \ NZM(x,y)=nx + my[/latex]
Treba li ju dokazati? (Kako to ide?)
Sama definicija mi NZM mi ništa ne znači jer ne kaže da je NZM u zbroju.
| 5ra (napisa): | Ako imamo skup cijelih brojeva Z, kako dokazati da je <x>+<y>=<nzm(x,y)>. jedan smjer mi jasan, ali ovaj da je <nzm(x,y)> podskup od <x>+<y> nemogu dobiti.
to je zadatak 16 u skripti. jel zna netko?
 |
Za smjer dokaza koji je 5ra-u jasan, imam nekih pitanja.
Dakle, dokaz za 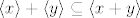
Koliko detaljno to treba? Pretpostavljam da se koristi ona tvrdnja:
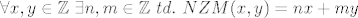
Treba li ju dokazati? (Kako to ide?)
Sama definicija mi NZM mi ništa ne znači jer ne kaže da je NZM u zbroju.
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
SvekY
Forumaš(ica)


Pridružen/a: 21. 11. 2003. (23:44:22)
Postovi: (FF)16
Spol: 
Lokacija: unitarni vektorski prostor
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Blizzard
Forumaš(ica)

Pridružen/a: 19. 10. 2006. (20:17:17)
Postovi: (121)16
Spol: 
Lokacija: u sjeni....
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
5ra
Forumaš(ica)


Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
5ra
Forumaš(ica)


Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
5ra
Forumaš(ica)


Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
 Postano: 14:59 ned, 6. 7. 2008 Naslov: Postano: 14:59 ned, 6. 7. 2008 Naslov: |
    |
|
|
enivejz, asistent Najman dao kontraprimjer
da bi ovo sve vrijedilo A mora imat jedinicu za mnozenje jer inace kontraprimjer
A=2Z, I=4Z, J=6Z
I+J=A,IJ=24Z.IpresjekJ=12Z
pak ako A ima jedinicu za mnozenje
lako se dokaze da je IJ podskup IpresjekJ jer za i€I,j€J imamo
ij€J jer je iJ poskup od J jer je J ideal
isto i s druge strane pa lako prva inkluzija
a sad dokazat da je IpresjekJ podskup IJ
uzmi element d iz presjeka
posto A=I+J i A ima jedinicu onda 1=i+j za neke i€I,j€J
sada je d= (i+j)d= id+jd=id+dj (jer je komutativan) i sad jer je d iz J imamo id€IJ i jer je d iz I imamo dj€IJ a posto je IJ grupa na zbrajanje je (id+dj)€IJ
eto, jedna briga manje :P
enivejz, asistent Najman dao kontraprimjer
da bi ovo sve vrijedilo A mora imat jedinicu za mnozenje jer inace kontraprimjer
A=2Z, I=4Z, J=6Z
I+J=A,IJ=24Z.IpresjekJ=12Z
pak ako A ima jedinicu za mnozenje
lako se dokaze da je IJ podskup IpresjekJ jer za i€I,j€J imamo
ij€J jer je iJ poskup od J jer je J ideal
isto i s druge strane pa lako prva inkluzija
a sad dokazat da je IpresjekJ podskup IJ
uzmi element d iz presjeka
posto A=I+J i A ima jedinicu onda 1=i+j za neke i€I,j€J
sada je d= (i+j)d= id+jd=id+dj (jer je komutativan) i sad jer je d iz J imamo id€IJ i jer je d iz I imamo dj€IJ a posto je IJ grupa na zbrajanje je (id+dj)€IJ
eto, jedna briga manje 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
teh_pwnerer
Forumaš(ica)

Pridružen/a: 02. 02. 2006. (19:06:27)
Postovi: (62)16
|
 Postano: 17:37 ned, 6. 7. 2008 Naslov: Postano: 17:37 ned, 6. 7. 2008 Naslov: |
    |
|
|
[quote="5ra"]jedno teorijsko pitanje.
to je mislim zadatak 18 u skripti, uglavnom:
ako su I i J ideali koji su relativno prosti, znači I+J=R i R je komutativan prsten treba dokazati da je I presjek J=IJ.
da je IJ podskup od I presjek J mi je jasno, ali druga inkluzija me muči... jel zna netko?[/quote]
Op, ipak je krivo. ^^
| 5ra (napisa): | jedno teorijsko pitanje.
to je mislim zadatak 18 u skripti, uglavnom:
ako su I i J ideali koji su relativno prosti, znači I+J=R i R je komutativan prsten treba dokazati da je I presjek J=IJ.
da je IJ podskup od I presjek J mi je jasno, ali druga inkluzija me muči... jel zna netko? |
Op, ipak je krivo. ^^
Zadnja promjena: teh_pwnerer; 22:24 ned, 6. 7. 2008; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
|

















