| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Bug
Forumaš(ica)
Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
 Postano: 11:02 ned, 29. 6. 2008 Naslov: |
    |
|
|
Nemam skener ni ništa slično pa ti mogu objasnit što se u tom radi :)
Dakle, imamo neki skup točaka (xi,yi) za i=1,2,...,n. Kad se nacrtaju te točke unutar koordinatnog sustava one su raspršene, a mi želimo taj skup točaka aproksimirati nekom fjom f t.d. f(xi) približno = yi za svaki i.
Ustvari želimo minimalizirat | f(xi)-yi | za svaki i.
| f(xi) - yi |= korijen ( (f(xi) - yi)^2 ) pa ćemo mi minimalizirat ovaj kvadrat, tj želimo da
[latex]\sum_{i=1}^{n}{ (f(x_i) - y_i)^2} [/latex] bude minimalna moguća. Neka je recimo f(x)=ax+b ( tj želimo točke aproksimirat pravcem).
Sada trebamo minimalizirat
[latex]\sum_{i=1}^{n}{ (a \cdot x_i + b - y_i)^2}[/latex], tu su nam a i b nepoznanice.
Pošto se radi o traženju minimuma, za to nam koriste stacionarne točke, tj nultočke derivacije. [b]( pitanje od mene: zašto kad deriviramo dođe baš minimum, a ne maximum?)[/b]
Pa deriviramo po a i po b i dobivamo sustav:
[latex]\sum_{i=1}^{n}{ (a \cdot x_i + b - y_i) \cdot xi}=0[/latex]
[latex]\sum_{i=1}^{n}{ (a \cdot x_i + b - y_i)}=0[/latex]
sa nepoznanicama a,b. Sad se to raspiše i dobiju se dvije jednadžbe s dvije nepoznanice i to je lako rješivo.
I jel može netko objasnit onu matričnu formulaciju, pomoću nekog zadatka iz zadaće recimo... to bi moglo bit korisno ak zakompliciraju nešto...
Nemam skener ni ništa slično pa ti mogu objasnit što se u tom radi 
Dakle, imamo neki skup točaka (xi,yi) za i=1,2,...,n. Kad se nacrtaju te točke unutar koordinatnog sustava one su raspršene, a mi želimo taj skup točaka aproksimirati nekom fjom f t.d. f(xi) približno = yi za svaki i.
Ustvari želimo minimalizirat | f(xi)-yi | za svaki i.
| f(xi) - yi |= korijen ( (f(xi) - yi)^2 ) pa ćemo mi minimalizirat ovaj kvadrat, tj želimo da
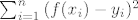 bude minimalna moguća. Neka je recimo f(x)=ax+b ( tj želimo točke aproksimirat pravcem).
Sada trebamo minimalizirat
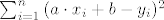 , tu su nam a i b nepoznanice.
Pošto se radi o traženju minimuma, za to nam koriste stacionarne točke, tj nultočke derivacije. ( pitanje od mene: zašto kad deriviramo dođe baš minimum, a ne maximum?)
Pa deriviramo po a i po b i dobivamo sustav:
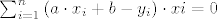
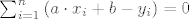
sa nepoznanicama a,b. Sad se to raspiše i dobiju se dvije jednadžbe s dvije nepoznanice i to je lako rješivo.
I jel može netko objasnit onu matričnu formulaciju, pomoću nekog zadatka iz zadaće recimo... to bi moglo bit korisno ak zakompliciraju nešto...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Bug
Forumaš(ica)
Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol:
Lokacija: Kako kad!!
|
|
| [Vrh] |
|
candica
Forumaš(ica)
Pridružen/a: 26. 08. 2007. (19:04:03)
Postovi: (1A)16
|
| Postano: 17:08 ned, 29. 6. 2008 Naslov: |
|
|
|
Ovo su dva zadatka sa vježbi!
Nadam se da će pomoći!
Ovo su dva zadatka sa vježbi!
Nadam se da će pomoći!
_________________ 
| Description: |
|
| Filesize: |
107.57 KB |
| Viewed: |
491 Time(s) |
|
| Description: |
|
| Filesize: |
107.1 KB |
| Viewed: |
477 Time(s) |
|
| Description: |
|
| Filesize: |
102.79 KB |
| Viewed: |
444 Time(s) |
|
|
|
| [Vrh] |
|
ma
Forumaš(ica)
Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol:
|
|
| [Vrh] |
|
5ra
Forumaš(ica)
Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
|
| [Vrh] |
|
ß
Forumaš(ica)
Pridružen/a: 29. 07. 2006. (15:29:06)
Postovi: (115)16
Spol:
Lokacija: Graveyard Mountain Home
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
woodstock
Forumaš(ica)
Pridružen/a: 10. 11. 2006. (23:52:04)
Postovi: (99)16
Spol:
|
| Postano: 10:39 pon, 30. 6. 2008 Naslov: |
|
|
|
jel može netko ovo riješit? :
Odredite koeficijente a, b i c ako podatke
xk -5 -3 -2 1 3
fk 21.6 14.4 10.8 0 -7.2
aproksimiramo funkcijom g(x) = ax2 + bx + c koristeći metodu najmanjih kvadrata.
ja dobivam a=0, b=-3,6, c=3,6, što nije točno... :?
hvala
jel može netko ovo riješit? :
Odredite koeficijente a, b i c ako podatke
xk -5 -3 -2 1 3
fk 21.6 14.4 10.8 0 -7.2
aproksimiramo funkcijom g(x) = ax2 + bx + c koristeći metodu najmanjih kvadrata.
ja dobivam a=0, b=-3,6, c=3,6, što nije točno... 
hvala
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
goc
Forumaš(ica)
Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
| Postano: 16:29 pon, 30. 6. 2008 Naslov: |
|
|
|
[quote="woodstock"]jel može netko ovo riješit? :
Odredite koeficijente a, b i c ako podatke
xk -5 -3 -2 1 3
fk 21.6 14.4 10.8 0 -7.2
aproksimiramo funkcijom g(x) = ax2 + bx + c koristeći metodu najmanjih kvadrata.
ja dobivam a=0, b=-3,6, c=3,6, što nije točno... :?
hvala[/quote]
bas malo gledam brojeve
-5*(-3.6)+3.6=21.6
-3*(-3.6)+3.6=14.4
-2*(-3.6)+3.6=10.8
1*(-3.6)+3.6=0
3*(-3.6)+3.6=-7.2
sto bi znacilo da je rjesenje 0, -3.6, 3.6 apsolutno tocno :) sta god da pisalo negdje gdje si provjeravao rjesenja ;)
| woodstock (napisa): | jel može netko ovo riješit? :
Odredite koeficijente a, b i c ako podatke
xk -5 -3 -2 1 3
fk 21.6 14.4 10.8 0 -7.2
aproksimiramo funkcijom g(x) = ax2 + bx + c koristeći metodu najmanjih kvadrata.
ja dobivam a=0, b=-3,6, c=3,6, što nije točno...
hvala |
bas malo gledam brojeve
-5*(-3.6)+3.6=21.6
-3*(-3.6)+3.6=14.4
-2*(-3.6)+3.6=10.8
1*(-3.6)+3.6=0
3*(-3.6)+3.6=-7.2
sto bi znacilo da je rjesenje 0, -3.6, 3.6 apsolutno tocno sta god da pisalo negdje gdje si provjeravao rjesenja 
|
|
| [Vrh] |
|
woodstock
Forumaš(ica)
Pridružen/a: 10. 11. 2006. (23:52:04)
Postovi: (99)16
Spol:
|
|
| [Vrh] |
|
arya
Forumaš(ica)
Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
|
| [Vrh] |
|
woodstock
Forumaš(ica)
Pridružen/a: 10. 11. 2006. (23:52:04)
Postovi: (99)16
Spol:
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)
Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol:
Lokacija: Over the roof
|
|
| [Vrh] |
|
|
