Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

bedasto pitanje
WWW:
Idite na 1, 2, 3, 4, 5  Sljedeće
Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 2. godine -> Diferencijalni račun i integrali funkcija više varijabli
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
Bug
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: muško
Sarma = la pohva - posuda
20 = 35 - 15
Lokacija: Kako kad!!
PostPostano: 15:10 pon, 4. 2. 2008    Naslov: bedasto pitanje Citirajte i odgovorite
ako imamo d1d2 f(x,y) jel to znaci da je prvo derivirano po d1 ili po d2
ako imamo d1d2 f(x,y) jel to znaci da je prvo derivirano po d1 ili po d2



_________________
Everybody Dies...
Nobody is perfect...

Non scholae, sed vitae discimus
[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
Mr.Doe
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
Sarma = la pohva - posuda
20 = 50 - 30
PostPostano: 15:17 pon, 4. 2. 2008    Naslov: Citirajte i odgovorite
Ima li uopce kakve razlike (Schwartzov teorem :wink: ) ?
Ima li uopce kakve razlike (Schwartzov teorem Wink ) ?


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Bug
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: muško
Sarma = la pohva - posuda
20 = 35 - 15
Lokacija: Kako kad!!
PostPostano: 16:54 pon, 4. 2. 2008    Naslov: Citirajte i odgovorite
kako ovo izracunati?

[img]http://i29.tinypic.com/k2l6jd.jpg[/img]
kako ovo izracunati?




_________________
Everybody Dies...
Nobody is perfect...

Non scholae, sed vitae discimus
[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
arya
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
49 = 109 - 60
Lokacija: forum
PostPostano: 17:03 pon, 4. 2. 2008    Naslov: Citirajte i odgovorite
pomnožiš onu matricu 2*2 sa onom 2*1, ono prije zareza je to... dobiješ vektor stupac i to množiš skalarno sa vektorom stupcem (x,y), dakle prvu koord. sa x, drugu sa y i zbrojiš to :) i onda sve još puta 1/2... nadam se da je jasno :)
pomnožiš onu matricu 2*2 sa onom 2*1, ono prije zareza je to... dobiješ vektor stupac i to množiš skalarno sa vektorom stupcem (x,y), dakle prvu koord. sa x, drugu sa y i zbrojiš to Smile i onda sve još puta 1/2... nadam se da je jasno Smile



_________________
kalendar Bow to the left
Pa, ptica... Zar nije ocito? Hrcak
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail MSNM
Bug
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: muško
Sarma = la pohva - posuda
20 = 35 - 15
Lokacija: Kako kad!!
PostPostano: 17:24 pon, 4. 2. 2008    Naslov: Citirajte i odgovorite
jest, sarma up :D
jest, sarma up Very Happy



_________________
Everybody Dies...
Nobody is perfect...

Non scholae, sed vitae discimus
[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
petrat
Forumaš s poteškoćama u pisanju
Forumaš s poteškoćama u pisanju


Pridružen/a: 20. 12. 2005. (10:23:20)
Postovi: (33)16
Sarma = la pohva - posuda
26 = 42 - 16
PostPostano: 19:56 pon, 4. 2. 2008    Naslov: parcijalno deriviranje - oznake Citirajte i odgovorite
("po unutrasnjem") dakle po varijabli y se prvo derivira u slucaju

[latex]\partial_x \partial_y f(x,y)=\partial_x( \partial_y f(x,y) )[/latex].

Kod funkcije klase [latex]C^2[/latex] nije potrebno paziti na poredak parcijalnog deriviranja, tj.

[latex]\partial_x \partial_y f(x,y)=\partial_y\partial_x f(x,y)[/latex].
("po unutrasnjem") dakle po varijabli y se prvo derivira u slucaju

.

Kod funkcije klase nije potrebno paziti na poredak parcijalnog deriviranja, tj.

.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
mladac
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: žensko
Sarma = la pohva - posuda
34 = 91 - 57
Lokacija: zg
PostPostano: 11:37 pet, 15. 2. 2008    Naslov: Citirajte i odgovorite
Df(1,−1)(2, 1) = −4.

može li mi neko objasnit kak to dobijem?
zadnji kolokvij 1.c zadatak?
netreba baš taj nego ono princip rješavanja.
mislila da znam, ispalo da ne znam, pa pitam :oops:
Df(1,−1)(2, 1) = −4.

može li mi neko objasnit kak to dobijem?
zadnji kolokvij 1.c zadatak?
netreba baš taj nego ono princip rješavanja.
mislila da znam, ispalo da ne znam, pa pitam Embarassed



_________________
potpis
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
RonnieColeman
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: muško
Sarma = la pohva - posuda
6 = 45 - 39
Lokacija: |R^3
PostPostano: 13:28 pet, 15. 2. 2008    Naslov: Citirajte i odgovorite
Ispituješ diferencijabilnost funkcije u problematičnoj točki(točka u čijoj okolini su točke drugačije definirane nego u njoj samoj) na način da tražiš sve parcijalne derivacije u toj točki(po definiciji parcijalnih derivacija).

Ako se ispostavi da sve parcijalne derivacije u toj točki postoje [b]i[/b] da su neprekidne onda zaključuješ da je funkcija diferencijabilna u toj točki.

Ako se ispostavi da ne postoje sve parcijalne derivacije onda funkcija nije dfb u toj točki.

Ako se ispostavi da postoje sve parcijalne derivacije, a nisu sve neprekidne onda [b]ne[/b] zaključuješ da funkcija nije dfb u toj točki.

Jedini preostali način, u tom slučaju, da ispitaš dfb funkcije u toj točki je nalaženjem kandidata za diferencijal(Jacobijeva matrica čiji su elementi parcijalne derivacije funkcije u točki kojoj diferencijabilnost ispituješ) i ispitivanje diferencijabilnosti po definiciji(limes kvocijenta normi mora ići u nulu).
Ispituješ diferencijabilnost funkcije u problematičnoj točki(točka u čijoj okolini su točke drugačije definirane nego u njoj samoj) na način da tražiš sve parcijalne derivacije u toj točki(po definiciji parcijalnih derivacija).

Ako se ispostavi da sve parcijalne derivacije u toj točki postoje i da su neprekidne onda zaključuješ da je funkcija diferencijabilna u toj točki.

Ako se ispostavi da ne postoje sve parcijalne derivacije onda funkcija nije dfb u toj točki.

Ako se ispostavi da postoje sve parcijalne derivacije, a nisu sve neprekidne onda ne zaključuješ da funkcija nije dfb u toj točki.

Jedini preostali način, u tom slučaju, da ispitaš dfb funkcije u toj točki je nalaženjem kandidata za diferencijal(Jacobijeva matrica čiji su elementi parcijalne derivacije funkcije u točki kojoj diferencijabilnost ispituješ) i ispitivanje diferencijabilnosti po definiciji(limes kvocijenta normi mora ići u nulu).



_________________
...He never had looked less like captain of any-thing, even his own soul.
[Vrh]
Korisnički profil Pošaljite privatnu poruku
mladac
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: žensko
Sarma = la pohva - posuda
34 = 91 - 57
Lokacija: zg
PostPostano: 14:35 pet, 15. 2. 2008    Naslov: Citirajte i odgovorite
ak je ovo odgovor na moje pitanje, nisam to pitala 8)
ak je ovo odgovor na moje pitanje, nisam to pitala Cool



_________________
potpis
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
arya
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
49 = 109 - 60
Lokacija: forum
PostPostano: 15:32 pet, 15. 2. 2008    Naslov: Citirajte i odgovorite
odrediš jacobijevu matricu ( to valjda znaš :) ), ak točka nije problematična ( a (1,-1) nije bila), uvrstišu tu matricu 1 i -1 i to ti je Df(1,-1)... običan linearni operator, sa R2 u R1 :) i odrediš kak djeluje na vektor (2,1)... linearna, niš drugo :) množiš matricu formata 1*2 sa vektorom iz R2, dakle 2*1... i dobit ćeš neki broj... valjda -4, ak je već tako ispalo :)
odrediš jacobijevu matricu ( to valjda znaš Smile ), ak točka nije problematična ( a (1,-1) nije bila), uvrstišu tu matricu 1 i -1 i to ti je Df(1,-1)... običan linearni operator, sa R2 u R1 Smile i odrediš kak djeluje na vektor (2,1)... linearna, niš drugo Smile množiš matricu formata 1*2 sa vektorom iz R2, dakle 2*1... i dobit ćeš neki broj... valjda -4, ak je već tako ispalo Smile



_________________
kalendar Bow to the left
Pa, ptica... Zar nije ocito? Hrcak
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail MSNM
mladac
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: žensko
Sarma = la pohva - posuda
34 = 91 - 57
Lokacija: zg
PostPostano: 16:24 pet, 15. 2. 2008    Naslov: Citirajte i odgovorite
tak sam radila. onda ispada da sam krivo množila :roll:
bože nekad sam fakat tuka
tak sam radila. onda ispada da sam krivo množila Rolling Eyes
bože nekad sam fakat tuka



_________________
potpis
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
ma
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: muško
Sarma = la pohva - posuda
58 = 89 - 31
PostPostano: 17:38 pet, 15. 2. 2008    Naslov: Citirajte i odgovorite
sljedeće se pitanje može smatrati bedastim, pa je ova tema adekvatna \:D/ .
naime, nikako ne mogu dokazati da je [latex]\text{Int} A[/latex] otvoren skup u [latex]\mathbb{R}^n[/latex]. piše da slijedi direktno iz definicije, u što vjerujem, ali muči me već neko vrijeme, pa molim dobre ljude za pomoć. :whistle2:
sljedeće se pitanje može smatrati bedastim, pa je ova tema adekvatna Dancing .
naime, nikako ne mogu dokazati da je 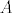otvoren skup u . piše da slijedi direktno iz definicije, u što vjerujem, ali muči me već neko vrijeme, pa molim dobre ljude za pomoć. Whistle



_________________
ima let u finish
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Mr.Doe
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
Sarma = la pohva - posuda
20 = 50 - 30
PostPostano: 17:49 pet, 15. 2. 2008    Naslov: Citirajte i odgovorite
Nema bedastih pitanja, samo bedastih odgovora (ja se nadam da moje nece biti takvo :lol: )

[latex]\displaystyle Int A=\bigcup_{U\subseteq A,~U\textrm{~otvoren~}} U[/latex], pa proizvoljna unija otvorenih skupova u [latex]\mathbb{R}^n[/latex] je .... (nadam se da dalje znate sami 8) )
Nema bedastih pitanja, samo bedastih odgovora (ja se nadam da moje nece biti takvo Laughing )

, pa proizvoljna unija otvorenih skupova u je .... (nadam se da dalje znate sami Cool )


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Nori
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 01. 10. 2006. (18:41:07)
Postovi: (E5)16
Spol: žensko
Sarma = la pohva - posuda
22 = 34 - 12
PostPostano: 17:51 pet, 15. 2. 2008    Naslov: Citirajte i odgovorite
Koliko se ja sjecam, definicija interiora od skupa A je da je to najveci OTVORENI skup sadrzan u A, pa mislim da se od tuda vidi....
Koliko se ja sjecam, definicija interiora od skupa A je da je to najveci OTVORENI skup sadrzan u A, pa mislim da se od tuda vidi....



_________________
Meni mama neda da.... Pričam sa dječacima... meni mama neda to-A što?-Jer kaže da je opasno!
[Vrh]
Korisnički profil Pošaljite privatnu poruku
ma
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: muško
Sarma = la pohva - posuda
58 = 89 - 31
PostPostano: 17:52 pet, 15. 2. 2008    Naslov: Citirajte i odgovorite
hvala, ali to mi je jasno. zanima me baš kako pokazati da otvorenost slijedi iz definicije. :-k
hvala, ali to mi je jasno. zanima me baš kako pokazati da otvorenost slijedi iz definicije. Think



_________________
ima let u finish
[Vrh]
Korisnički profil Pošaljite privatnu poruku
ma
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: muško
Sarma = la pohva - posuda
58 = 89 - 31
PostPostano: 17:54 pet, 15. 2. 2008    Naslov: Citirajte i odgovorite
[quote="Nori"]Koliko se ja sjecam, definicija interiora od skupa A je da je to najveci OTVORENI skup sadrzan u A, pa mislim da se od tuda vidi....[/quote]

ne. definicija je - interior je skup svih unutrašnjih točaka. [url=http://web.math.hr/nastava/difraf/dif/p_o3.pdf]str. 9.[/url]
Nori (napisa):
Koliko se ja sjecam, definicija interiora od skupa A je da je to najveci OTVORENI skup sadrzan u A, pa mislim da se od tuda vidi....


ne. definicija je - interior je skup svih unutrašnjih točaka. str. 9.



_________________
ima let u finish
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Mr.Doe
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
Sarma = la pohva - posuda
20 = 50 - 30
PostPostano: 17:59 pet, 15. 2. 2008    Naslov: Citirajte i odgovorite
[quote="Mr.Doe"]
[latex]\displaystyle Int A~\underline{:=}~\bigcup_{U\subseteq A,~U\textrm{~otvoren~}} U[/latex], pa proizvoljna unija otvorenih skupova u [latex]\mathbb{R}^n[/latex] je .... (nadam se da dalje znate sami 8) )[/quote]

Mislio sa da ce biti jasno, ocigledno nije bilo, dakle kolegica nori je dobro rekla da je interiror najveci otvoreni skup sadrzan u tom skupu, sto je upravo ono sto sam napisao, a mislio sam da se sjecate da je proizvoljna unija otvorenih skupova ( u [latex]\mathbb{R}^n[/latex], sa standardnom topologijom ) otvoren skup, pa odavde slijedi trazena tvrdnja.
Mr.Doe (napisa):

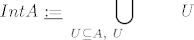, pa proizvoljna unija otvorenih skupova u je .... (nadam se da dalje znate sami Cool )


Mislio sa da ce biti jasno, ocigledno nije bilo, dakle kolegica nori je dobro rekla da je interiror najveci otvoreni skup sadrzan u tom skupu, sto je upravo ono sto sam napisao, a mislio sam da se sjecate da je proizvoljna unija otvorenih skupova ( u , sa standardnom topologijom ) otvoren skup, pa odavde slijedi trazena tvrdnja.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
rafaelm
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: muško
Sarma = la pohva - posuda
76 = 86 - 10
Lokacija: Zagreb
PostPostano: 17:59 pet, 15. 2. 2008    Naslov: Citirajte i odgovorite
[quote="ma"]hvala, ali to mi je jasno. zanima me baš kako pokazati da otvorenost slijedi iz definicije. :-k[/quote]

Interior skupa S je skup svih točaka oko kojih se može opisati otvorena kugla tako da cijela stane u S. Ali za svaku točku u toj kugli opet mozeš naći kuglu (malo manju :)) tako da cijela stane u veću (jer je kugla otvorena), znači da stane i u S. Pa je iz toga svaka točka veće kugle unutrašnja točka skupa S, pa je cijela veća kugla sadržana u interioru od S. To vrijedi za svaku točku iz interiora, pa je on otvoren skup.

Ne garantiram da ne može jednostavnije :?
ma (napisa):
hvala, ali to mi je jasno. zanima me baš kako pokazati da otvorenost slijedi iz definicije. Think


Interior skupa S je skup svih točaka oko kojih se može opisati otvorena kugla tako da cijela stane u S. Ali za svaku točku u toj kugli opet mozeš naći kuglu (malo manju Smile) tako da cijela stane u veću (jer je kugla otvorena), znači da stane i u S. Pa je iz toga svaka točka veće kugle unutrašnja točka skupa S, pa je cijela veća kugla sadržana u interioru od S. To vrijedi za svaku točku iz interiora, pa je on otvoren skup.

Ne garantiram da ne može jednostavnije Confused



_________________
Rafael Mrđen
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
ma
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: muško
Sarma = la pohva - posuda
58 = 89 - 31
PostPostano: 18:02 pet, 15. 2. 2008    Naslov: Citirajte i odgovorite
@Mr. Doe
a čuj... meni u skripti tako ne piše. dao sam link gore. ako je tako kako ti kažeš, onda mi je sve jasno. no, ja ne znam da li bih trebao vjerovati definiciji iz skripte koju koristi profesor ili definiciji koju mi da netko na forumu, a koja se u skripti zove propozicija :roll:
@Mr. Doe
a čuj... meni u skripti tako ne piše. dao sam link gore. ako je tako kako ti kažeš, onda mi je sve jasno. no, ja ne znam da li bih trebao vjerovati definiciji iz skripte koju koristi profesor ili definiciji koju mi da netko na forumu, a koja se u skripti zove propozicija Rolling Eyes



_________________
ima let u finish

Zadnja promjena: ma; 18:02 pet, 15. 2. 2008; ukupno mijenjano 1 put.
[Vrh]
Korisnički profil Pošaljite privatnu poruku
rafaelm
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: muško
Sarma = la pohva - posuda
76 = 86 - 10
Lokacija: Zagreb
PostPostano: 18:02 pet, 15. 2. 2008    Naslov: Citirajte i odgovorite
[quote="Mr.Doe"]
[latex]\displaystyle Int A~\underline{:=}~\bigcup_{U\subseteq A,~U\textrm{~otvoren~}} U[/latex][/quote]

To je jasno, ali smo mi kod prof. Tambače definirali interior kao skup svih unutarnjih točaka, pa držim da je kolega mislio na "tu" definiciju.
Mr.Doe (napisa):



To je jasno, ali smo mi kod prof. Tambače definirali interior kao skup svih unutarnjih točaka, pa držim da je kolega mislio na "tu" definiciju.



_________________
Rafael Mrđen
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 2. godine -> Diferencijalni račun i integrali funkcija više varijabli Vremenska zona: GMT + 01:00.
Idite na 1, 2, 3, 4, 5  Sljedeće
Stranica 1 / 5.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan