| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
|
| [Vrh] |
|
Vip
Forumaš(ica)

Pridružen/a: 12. 10. 2007. (17:53:31)
Postovi: (8E)16
Spol: 
|
|
| [Vrh] |
|
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
 Postano: 19:18 uto, 19. 1. 2010 Naslov: Postano: 19:18 uto, 19. 1. 2010 Naslov: |
    |
|
|
[quote="rafaelm"]Poledaj karakterizacije unitarnog i hermitskog operatora preko spektra. Ako je [latex]\lambda \in \sigma (U)[/latex], onda je [latex]\lambda[/latex] na jediničnoj kružnici u kompleksnoj ravnini, a [latex]\lambda + \frac{1}{2}[/latex] mora biti realan i pozitivan broj. Očito može biti jednino [latex]\lambda =1[/latex]. Dakle spektar takvog operatora je najviše jednočlan. Primjer: identiteta. [/quote]
Tako je ona napiusao, al mo li mi neko malo bolje objasnit i kako bi bilo da je umjesto 1/2, 1! Hvala!
| rafaelm (napisa): | Poledaj karakterizacije unitarnog i hermitskog operatora preko spektra. Ako je 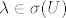 , onda je , onda je  na jediničnoj kružnici u kompleksnoj ravnini, a na jediničnoj kružnici u kompleksnoj ravnini, a 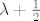 mora biti realan i pozitivan broj. Očito može biti jednino mora biti realan i pozitivan broj. Očito može biti jednino 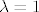 . Dakle spektar takvog operatora je najviše jednočlan. Primjer: identiteta. . Dakle spektar takvog operatora je najviše jednočlan. Primjer: identiteta. |
Tako je ona napiusao, al mo li mi neko malo bolje objasnit i kako bi bilo da je umjesto 1/2, 1! Hvala!
_________________
Everybody Dies...
Nobody is perfect...
Non scholae, sed vitae discimus
|
|
| [Vrh] |
|
_Neyni_
Forumaš(ica)


Pridružen/a: 17. 02. 2009. (17:31:17)
Postovi: (1C)16
Spol: 
|
|
| [Vrh] |
|
Željan
Forumaš(ica)
Pridružen/a: 10. 03. 2010. (22:37:50)
Postovi: (6)16
|
 Postano: 23:08 sri, 10. 3. 2010 Naslov: Postano: 23:08 sri, 10. 3. 2010 Naslov: |
    |
|
|
Lijep pozdrav svima,
pratim vaše rasprave pa se uvijek nađe nešto korisno... meni treba pomoć oko jednog zadatka pa ako bi netko mogao...
Treba provjeriti jesu li slijedeći realni vektorski prostori U unitarni uz pripadni skalarni produkt ( | ) : U x U --> R
a) U = R^3 (( x1,x2,x3) | (y1,y2,y3)) = x1 + 2x2 + x3y3
b) U = R^3 (( x1,x2,x3) | (y1,y2,y3)) = x1y2 + x2y1 + 3x3y3
c) U = R ( x | y ) = 2xy + x
Eto, ne znam ni kako započet pa bi volio ako može malo detaljnije :roll: ...
Lijep pozdrav svima,
pratim vaše rasprave pa se uvijek nađe nešto korisno... meni treba pomoć oko jednog zadatka pa ako bi netko mogao...
Treba provjeriti jesu li slijedeći realni vektorski prostori U unitarni uz pripadni skalarni produkt ( | ) : U x U --> R
a) U = R^3 (( x1,x2,x3) | (y1,y2,y3)) = x1 + 2x2 + x3y3
b) U = R^3 (( x1,x2,x3) | (y1,y2,y3)) = x1y2 + x2y1 + 3x3y3
c) U = R ( x | y ) = 2xy + x
Eto, ne znam ni kako započet pa bi volio ako može malo detaljnije  ... ...
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 0:11 čet, 11. 3. 2010 Naslov: Postano: 0:11 čet, 11. 3. 2010 Naslov: |
    |
|
|
[quote="Željan"]Lijep pozdrav svima,
pratim vaše rasprave pa se uvijek nađe nešto korisno... meni treba pomoć oko jednog zadatka pa ako bi netko mogao...
Treba provjeriti jesu li slijedeći realni vektorski prostori U unitarni uz pripadni skalarni produkt ( | ) : U x U --> R
a) U = R^3 (( x1,x2,x3) | (y1,y2,y3)) = x1 + 2x2 + x3y3
b) U = R^3 (( x1,x2,x3) | (y1,y2,y3)) = x1y2 + x2y1 + 3x3y3
c) U = R ( x | y ) = 2xy + x
Eto, ne znam ni kako započet pa bi volio ako može malo detaljnije :roll: ...[/quote]
Trebaš provjeriti da li je funkcija [latex](\cdot |\cdot)\colon U\times U\to\mathbb{R}[/latex] zbilja skalarni produkt, tj. provjeriti da li zadovoljava sva tri aksioma skalarnog produkta: (konjugiranu) simetriju, linearnost u prvoj varijabli i pozitivnu definitnost.
Npr. pod c) očito ne vrijedi [latex](x|y)=(y|x)[/latex] jer je [latex](1|0)=1[/latex], a [latex](0|1)=0[/latex] pa [latex]\mathbb{R}[/latex] uz tako zadan skalarni produkt nije unitaran prostor.
| Željan (napisa): | Lijep pozdrav svima,
pratim vaše rasprave pa se uvijek nađe nešto korisno... meni treba pomoć oko jednog zadatka pa ako bi netko mogao...
Treba provjeriti jesu li slijedeći realni vektorski prostori U unitarni uz pripadni skalarni produkt ( | ) : U x U → R
a) U = R^3 (( x1,x2,x3) | (y1,y2,y3)) = x1 + 2x2 + x3y3
b) U = R^3 (( x1,x2,x3) | (y1,y2,y3)) = x1y2 + x2y1 + 3x3y3
c) U = R ( x | y ) = 2xy + x
Eto, ne znam ni kako započet pa bi volio ako može malo detaljnije  ... ... |
Trebaš provjeriti da li je funkcija 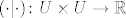 zbilja skalarni produkt, tj. provjeriti da li zadovoljava sva tri aksioma skalarnog produkta: (konjugiranu) simetriju, linearnost u prvoj varijabli i pozitivnu definitnost. zbilja skalarni produkt, tj. provjeriti da li zadovoljava sva tri aksioma skalarnog produkta: (konjugiranu) simetriju, linearnost u prvoj varijabli i pozitivnu definitnost.
Npr. pod c) očito ne vrijedi 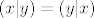 jer je jer je 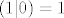 , a , a 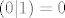 pa pa  uz tako zadan skalarni produkt nije unitaran prostor. uz tako zadan skalarni produkt nije unitaran prostor.
_________________
The Dude Abides
|
|
| [Vrh] |
|
Željan
Forumaš(ica)
Pridružen/a: 10. 03. 2010. (22:37:50)
Postovi: (6)16
|
|
| [Vrh] |
|
behemont
Forumaš(ica)

Pridružen/a: 12. 02. 2008. (21:21:19)
Postovi: (124)16
Spol: 
|
 Postano: 16:09 čet, 11. 3. 2010 Naslov: Postano: 16:09 čet, 11. 3. 2010 Naslov: |
    |
|
|
a) nije...kad bi bio trebalo bi vrijediti [latex]((1,0,0)|(0,0,1))=((0,0,1)|(1,0,0))[/latex]. Lijeva strana je jednaka [latex]1[/latex], a desna [latex]0[/latex], pa nemogu biti jednake. Potpuno analogno ide i [latex]b)[/latex].
a) nije...kad bi bio trebalo bi vrijediti 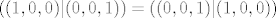 . Lijeva strana je jednaka . Lijeva strana je jednaka  , a desna , a desna  , pa nemogu biti jednake. Potpuno analogno ide i , pa nemogu biti jednake. Potpuno analogno ide i 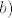 . .
|
|
| [Vrh] |
|
|










